台形は四角形の仲間で、「向かい合った一組の辺が平行」という特徴があります。
台形の面積を求める公式は長方形や平行四辺形の面積の公式に比べ、使う機会が少ないかもしれません。
一度どんな公式だったか、確認してみませんか?
問題
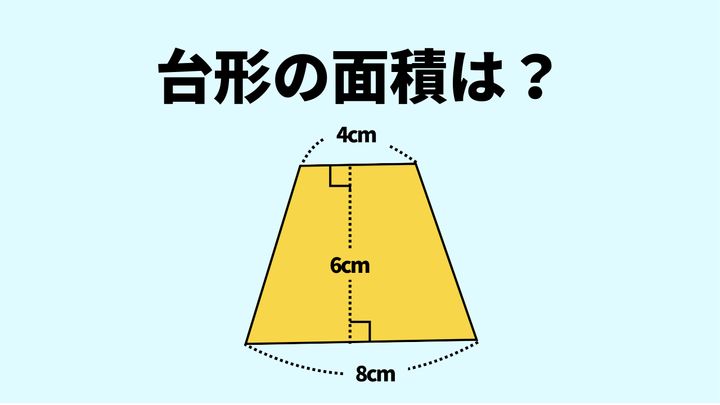
次の台形の面積を求めなさい。
※長さや面積の縮尺は、必ずしも正確に描かれていません。
解答
正解は、「36cm2」です。
台形の面積の公式、無事思い出せたでしょうか?
次の「ポイント」では、台形の面積の公式を使ったスタンダードな方法にプラスして、「三角形」と「平行四辺形」の面積を利用した答えの出し方も紹介します。
台形の面積のいろいろな求め方を覚えておくと、公式の理解にもつながりますよ。正解した人も、ぜひご覧ください。
ポイント
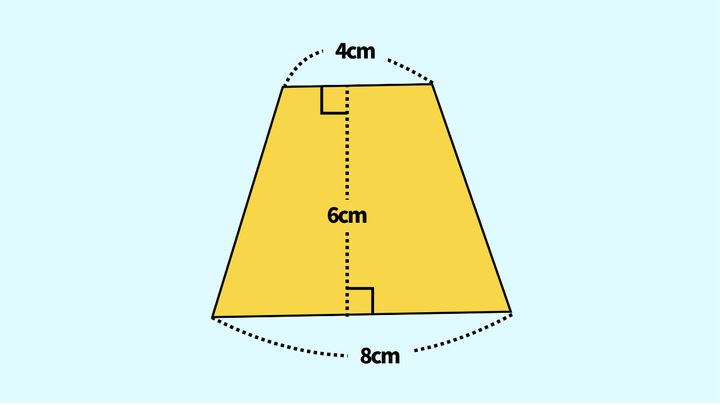
まず、この問題のポイントとなる「台形の面積の公式」を確認しておきましょう。
台形の面積=(上底+下底)×高さ÷2
今回の台形の図であれば、上底が4cm、下底が8cm、高さが6cmだと考えればOKです。
それぞれの数を公式に当てはめれば答えが出ます。
(上底+下底)×高さ÷2
=(4cm+8cm)×6cm÷2
=12cm×6cm÷2
=36cm2
【おまけ】三角形と平行四辺形を作って台形の面積を求める
もし、この台形の面積の公式がどうしても思い出せなかったら、どうしたらよいのでしょうか。
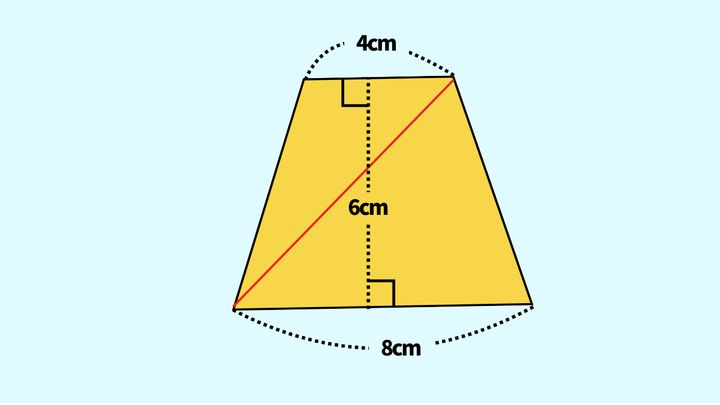
そんなときは、台形を三角形に分割して考えてみましょう。
まず、台形を以下の図の赤線で二つに切ります。すると、底辺4cmで高さが6cmの三角形と、底辺8cmで高さが6cmの三角形ができます。
三角形の面積の公式は、底辺×高さ÷2なので、次の式で台形の面積を求めることができます。
4cm×6cm÷2+8cm×6cm÷2←二つの三角形の面積を求めて足す
=12cm2+24cm2
=36cm2
※×6cm÷2に注目して変形すると、台形の面積の公式を使ったときと同じ式ができますよ。
4cm×6cm÷2+8cm×6cm÷2
=(4cm+8cm)×6cm÷2
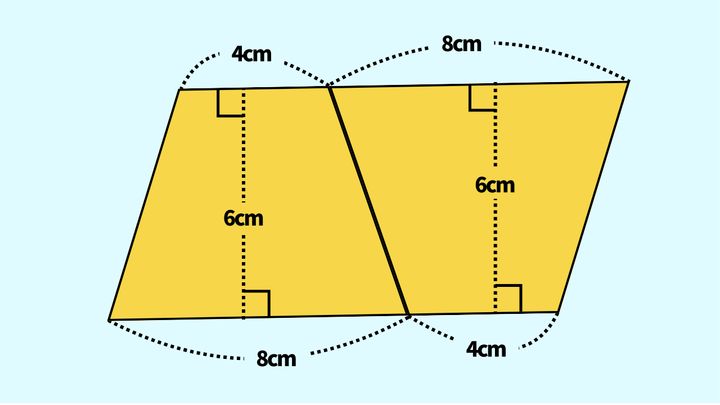
さらに、台形の面積は平行四辺形の面積の公式を使って求めることもできます。
まず、台形をコピーして回転させ、二つの台形をくっつけましょう。すると、以下の図のような平行四辺形が作れます。
平行四辺形の面積の公式は、底辺×高さですから、台形の面積は次の式で求められます。
(8cm+4cm)×6cm←平行四辺形の面積
=72cm2
72cm2÷2←平行四辺形は台形の2倍の面積だから2で割る
=36cm2←台形の面積
※二つの式を連続で書くと、台形の面積の公式を使ったときと同じ式ができます。
(8cm+4cm)×6cm÷2
どの方法を使っても、答えはすべて同じ36cm2になりますね。
まとめ
台形の面積の公式は、「(上底+下底)×高さ÷2」です。
もし、この公式を忘れてしまっても、三角形や平行四辺形の面積の公式を覚えていれば、答えを出すことができます。
図形の問題にはいろいろなアプローチの仕方があります。どうしても必要な公式を思い出せないときは、別の公式を応用して計算できないか、考えてみてくださいね。
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。
文(編集):VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。
スピード勝負!他の問題にも挑戦しよう!