<上方倍音列表(自然倍音列)>
自然倍音の第16倍音まで一覧表にまとめました。

・1=1倍音=基音として、以降16倍音まで掲載。
・音名は24平均律の周波数に基づく近似値で割り振り。
・緑色のセルは異名同音の列、例C#=Dbなど。
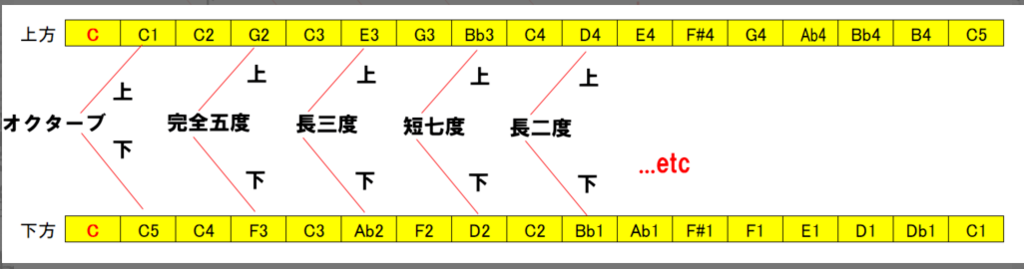
基音cのときの倍音を鍵盤で表すと、

<上方倍音列の基音からの音程>
1.基音
2.オクターブ(完全8度)
3.完全5度
4.オクターブ
5.長3度
6.完全5度
7.短7度
8.オクターブ
9.長9度
10.長3度
11.増11度
12.完全5度
13.短13度
14.短7度
15.長7度
16.オクターブ
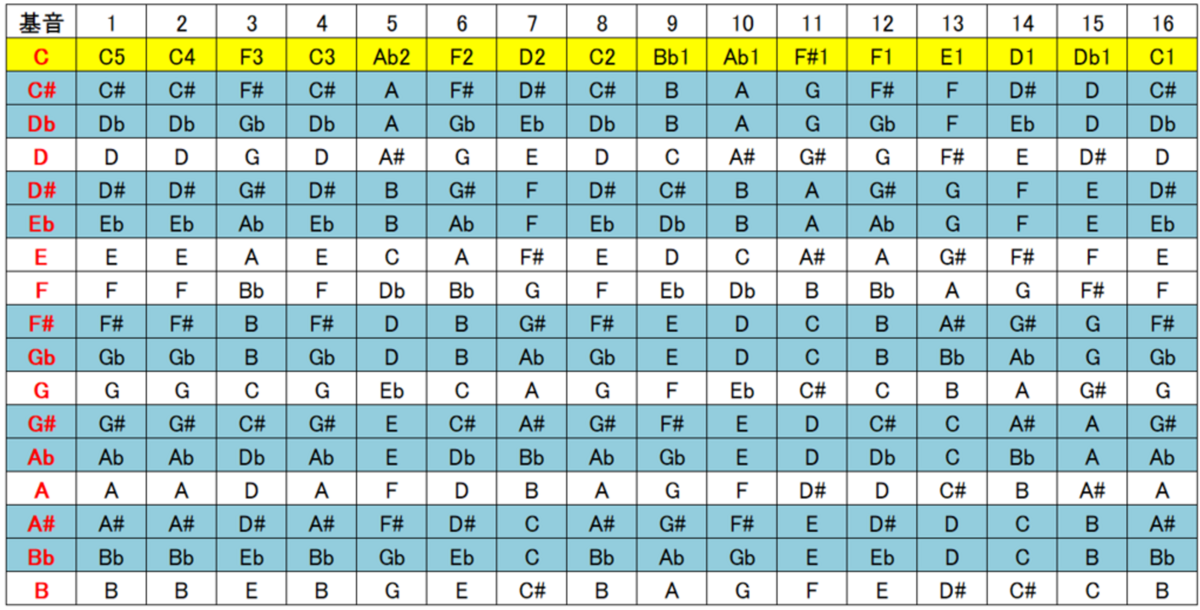
<下方倍音列表>
下方倍音列は、物理的な振動によって直接生じる集合音ではありません。
上方倍音が基音から生じる周波数列なのに対して、下方倍音は、上方倍音にcを持つ基音の序列を順に並べたものです。
この一覧表では、第16倍音が最も低いc1になるように書いてあります。青色のセルは異名同音の列です。
<下方倍音列の音程>
1.基音
2.オクターブ(完全8度)
3.完全4度
4.オクターブ
5.短6度
6.完全4度
7.長9度
8.オクターブ
9.短7度
10.短13度
11.増11度
12.完全4度
13.長3度
14.長9度
15.短9度
16.オクターブ
==音程関係図==![]()
「倍音」とは?
元々ピタゴラス学派が二つの音の弦の分割の比によって、「よく響く音」という概念を発見し、そこに古代ギリシャで使われていた、結合、連結など意味した「ἁρμός」という語から、ἁρμονία(harmonia)=調和する、といった意味合いが作られ定着していきました。
響く音という現象と自然の中のさまざまな調和について関連させて考える風潮が出来上がりました。
これはピアノの440Hzのaの音を鳴らした時のEQ画像です。

440.3hzのaの原音の他に882Hz、1327Hzの音等が出現しています。これが倍音です。左から、基音、第2倍音、第3倍音、だいたい第8倍音までここでは表示されていますね。自然音なら必ずこの倍音が入り、このそれぞれの倍音がどのくらいの割合で含まれているかで、その音の音色が決まります。人はピアノの音色を聴いているようで、ピアノの倍音群を聞いていたわけです。
そして17世紀にはガリレオやメルセンヌらによって、音の振動数が計算されています。メルセンヌの1636年の「Harmonie Universelle」には現代の倍音列の計算の元となる記述がされ、1701年のジョセフ・ソヴールの著書には下記のような表がすでに添付されています。ここでハーモニーと数理は、哲学や美学を超えて、数学的にさらに密接な関わりを見せます。
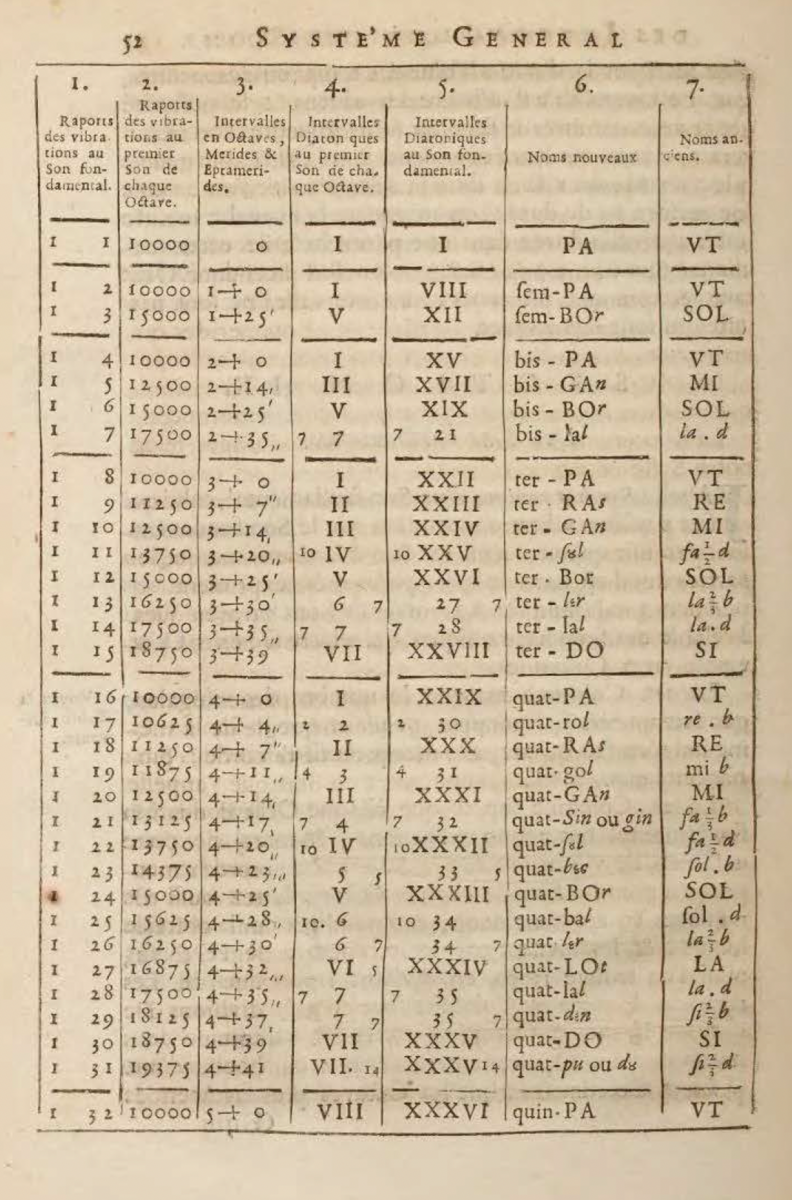 (引用)
(引用)
ここからラモーが『自然の諸原理に還元された和声論』にて音楽理論の中に組み込んで体系化しました。自然と音楽の要素が集合します。
ハーモニーすなわち美的調和であり、それは数の比率に関係している、と考えるのがセットになります。
関連用語の整理
また「overtone」という語自体は、ドイツ語の「Oberpartialtöne」からの省略借用語のようで、ヘルムホルツらが音響物理の方面から使い出した用語で、「基本周波数よりも高い共鳴周波数」を意味するようです。
日本ではこれを「倍音」と訳して使用していますが、パッと探せる範囲では、明治30年以降の「尋常中学科講義録 物理学」の中で、「基音より振動数の大きな音を倍音」という、とすでに書かれていますので、かなり早い段階でそのように訳されたのでしょう。

また明治41年、田辺尚雄著による「音響と音楽」において、「倍音またはハルモニックス」として紹介されているのが見られます。

12音の二つの領域
以下に示す内容は、拙論「不定調性論」に基づく独自の概念を含みます。
上方と下方の倍音の類似した性格から下記の不定調論における12音連関表が生まれました。これにより12音が三つの縦列と四つの横列に分けられたことで、12音の関係性がより対等になっていきました。

これらの三つのグループ分けについては、暇な折、下記もご参照ください。
倍音の中にある構造についてはこちら
12音連関表を活用した音集合表記法はこちら
近似値について
近似値による振り分けについて
拙論では、24平均律(1音をさらに半分に分けた微分音的スケール)における中点を目安とし、各倍音の周波数を最も近い音名に振り分ける方法を採用しています。
調律の基準や解釈によっては、「その音名に割り当てるのは適切か?」という議論も生じるでしょう。
その場合、各位が用いる調律システムや方法論に則って振り分けることをお勧めします。
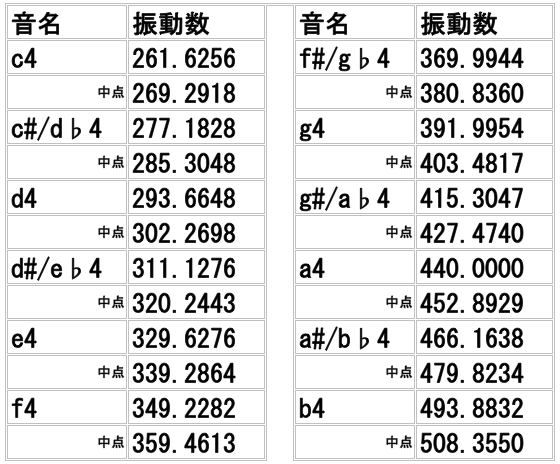
これによりどんな半端な振動数を持つ音も平均律の音名に振り分けて音楽表現が可能になります。
下方倍音の領域
響いているはずのない音への感応
たとえば、ピアノの鍵盤をひとつ打鍵したとき、部屋の隅の家具や装飾品、あるいは壁面が、わずかに共鳴しているように感じることがあります。
これは実際に測定された周波数としては可聴範囲に現れない、極めて微細な振動である可能性があります。
また、基音の下に存在するはずのない「下方倍音」が、知覚できない形で空間に存在しているのではないかと感じる瞬間があるかもしれません。
このような疑問は、数値や測定だけでは解き明かせない、音楽体験の感覚的領域に属するものです。
聴こえない音が与えるもの
人は、耳鳴りや幻聴といった「内耳的な音」を持ちます。
また、高熱時には、得体の知れない音楽や声が聞こえてくることがあります。それは夢うつつの中で、不安を和らげたり、心を鎮めたりする不思議な体験として残ることがあります。
これらは、物理的には「存在しない音」です。しかしそれを音として経験している自分という主体がいる事実は無視できません。
音の存在とは、単に空気の振動だけでなく、脳内に生じる構造、あるいは自己身体との共鳴によっても成り立ちうるという考え方です。
不定調性論における「存在しない音」
不定調性論(独自論です)では、こうした「実際には鳴っていないが、構造的・精神的には存在し得る音」を、音楽的構造を拡張する思考装置として扱います。シンプルにはそれらを全てに感応して音楽表現を執り行う因子となる心的反応を「音楽的なクオリア」と表現しています。
ある基音に対して、その「上方倍音列」だけでなく、数理的な「下方倍音列」を考えることで、音の連鎖や重なりの世界が、意識の中で多次元的に広がっていきます。
これは、現実には聞こえない音の存在を「証明」しようという試みではなく、
「聞こえない音を思考することで、聞こえる音の理解を拡張する」
という発想です。音を扱う個人が、「ああ、この音は私にとって、こういう関係性を持つ音なのだなぁ」と認識できることで、音存在への理解が、独自的に進めば、音楽表現もどんどん進むのではないか、と思うのです。なんとなくやるよりも。
認識されない共鳴
人間の耳には聞こえない低周波や超音波が、建物や人体に微細な影響を与えることがあると知られています。
私たちの体には数十兆の微生物が常在し、その活動音は本来極めて複雑であるはずですが、私たちはその音を知覚しないよう調整されています。
もし、これらの音をすべて「聞こえるようにされた」としたら、人は自らの身体に発狂するかもしれません。
音楽という営みは、こうした「認識されない共鳴」への感性を、丸っとひっくるめた上で、人間が安全に体験する一つの装置でもあると言えるでしょう。
音楽は人間のための意義であり、それを見つけられたこと、享受できることに感謝するだけでも制作時、演奏時、心が落ち着くのではないでしょうか。
音楽の輪郭を拡張する
不定調性論において、下方倍音とは単なるファンタジーではなく、
理論上存在しうる音を、音楽構造の中に意図的に導入するための枠組みとしています。
「存在しない音」を扱うことで、存在している音の背景にある構造や流れをより深く理解しようとする試みでもあります。
科学的事実ではなく、あくまで構造上の仮定として導入されるものであり、その意図と使い道が明確であるなら、音楽理論として十分に意味を持つと考えています。
そういうふうに宣言して意識の中に取り入れようとしている人がいる、と知っていただくだけで十分でしょう。
倍音列数理の深淵
私たちが「倍音」と呼ぶものは、整数比に基づく一連の音高であり、1:2:3:4…という自然数列に従って生成される周波数系列です。
この系列は、物理的には単純な振動の結果ですが、その音楽的意味付けは、時代や文化によって大きく異なってきました。
不定調性論では、倍音列を単に「音の並び」として捉えるのではなく、数学的関係の網として解釈することから出発します。
この網には方向性があり、また、上下対称性と非対称性を同時に孕んでいます。
上方倍音列の構造再確認
自然倍音列(上方倍音列)は、1(基音)を起点とし、以下のような周波数比を取ります。
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16 …
ここで重要なのは、倍音の増加に従って、平均律との乖離が顕著になるという点です。
たとえば、第3倍音(完全五度)や第5倍音(長三度)は、平均律と比較してごくわずかなズレしかありませんが、第7倍音(約968.8セント)は平均律のB♭と20セント以上の差を持ちます。
この差異は、調律体系によって扱いが分かれる要因ともなっています。
つまり、倍音列とは「常に純粋な音楽性を保証する構造」ではなく、音楽的判断を要求する数列です。
下方倍音列の理論的定義
不定調性論において導入される「下方倍音列」は、純粋には物理的に発生しないものです。
これは「ある基音を上方倍音として持つような仮想的基音」を、逆算によって導き出すことで構築されます。
数学的には、任意の倍音 𝑛に対して:
基音fのn倍音が現在の音であるとするなら、仮想的な下方基音はf/n
という形で表現されます
*1。
たとえば、現在の音が440Hz(A)であった場合、
・これを第2倍音とみなせば、仮想基音は220Hz(A)
・これを第4倍音とみなせば、110Hz(A)
・これを第5倍音とみなせば、88Hz(F付近)
というように、同じ音が異なる仮想基音に帰属する可能性を持ちます。
一つの音には無数の下方倍音的帰属関係が存在することになります。
これが不定調性論における「和音の不定性」や「音の多解釈性/多義性」の基盤のひとつになります。
倍音列音を実際の音楽に用いるとき、次の二つの考え方があります。
・発生した振動数音をそのまま用いる
倍音列は、平均律の振動数から見ると近似値です。第三倍音も本来数学的な一致を見ません。「倍音列の音を用いる」のであれば、この発生した値を微分音的にそのまま用いる必要があります。
・発生した振動数音を自己解釈して平均律音名、または各位の微分音律音名に当てはめて用いる
本来上方倍音列の中に"平均律の長三和音"は現れていません。
不定調性論は、あらゆる音を12音に振り分けて解釈して用います。私が平均律大好き人間だからです。倍音の秩序を用いたいのではなく、グルーピングの容易さ、解釈の整然さゆえに用いているだけで、倍音列を盲信しているわけではありません。
不定調性論の中での活用事例
不定調性論的方法論の中で見つけられる倍音列の数理を用いた例を列挙します。
■上下の倍音による完全結合領域から、12音連関表を作ることができる。
■発生音を組み合わせると、T-SD-D-Tの連結した世界が作れる、またこのことから、民族音楽的五音階の音世界と、西洋音楽的七音階の世界が表裏一体になる。 長調と短調世界が極まる。
等々。
領域の重合の解釈1
細々としたところでは連関性は無限に構築できます。
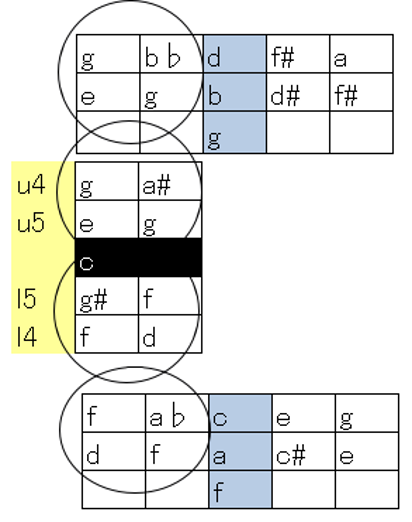
基音cの上方領域e,g,b♭音は、基音gの上方領域音b,dを生み出す下方倍音解釈が可能です。また基音cの下方倍音は、基音fの上方領域音を生み出す下方倍音解釈が可能です。このことから主要三和音が強く結びついていることを導き出し、独自論を作ることもできます。
また、
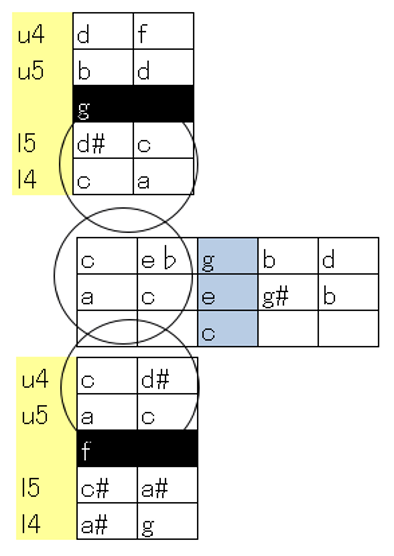
基音cの上方領域音e,gを生み出す下方倍音は、基音gとfのそれぞれ下方倍音、上方倍音解釈に該当させられます。ここから主和音の絶対性を導き出す独自論を作れます。
つまり、
bの下方音=b,e,g
cの上方音=c,e,g
cの下方倍=c,f,a♭
d♭の上方音=d♭,f,a♭

と連鎖していく、入れ子状の世界があります。そういう存在でよく知られている構造にフラクタクル構造です。世界の構造がこうした「連鎖」で構成されているなら、私たちの体も何らかの連鎖構造が支配していると言えます。
上記したように、倍音構造もいわば旋律的連鎖を見ることもできます。
cの上方音=c,e,g
はbの下方音=b,e,gに連鎖しやすく、
cの下方倍=c,f,a♭
はcの上方音=c,e,gに半音で連鎖しやすいです。
倍音列の連鎖は、まさに旋律の連鎖、音と音が連なっていく様を表現している、とも言えます。
領域の重合の解釈2
cの領域は上方倍音と下方倍音において螺旋構造のように半音程度ずれています。
cの上方領域↔︎cの下方領域は、互いに連鎖し、旋律を作ります。f↔︎e、a♭↔︎g等々。
このずれていることへの認識はすなわち人の感覚から見ると「整合性を作るために動かしたくなる気持ち」につながっていきます。もともと世界が捻れてずれて渦を巻いているなら、人も動いて、変化して、整合性を求め続けることが生きる目的となり、その類似品として音楽行為もそこに加えられているのでは??なんて考えてしまいます。
アリストテレスの「可能態(デュナミス)」と「現実態(エネルゲイア)」に相当するようにも思います。
概念は古代からあったのですが、人類はこういうことを認知しないで生活できる工夫が体内に備わっています。
動きについての欲求は可能性と認識で連鎖します。
一つの音を連鎖すると、それがまた新たな傾きを求める根拠になります。
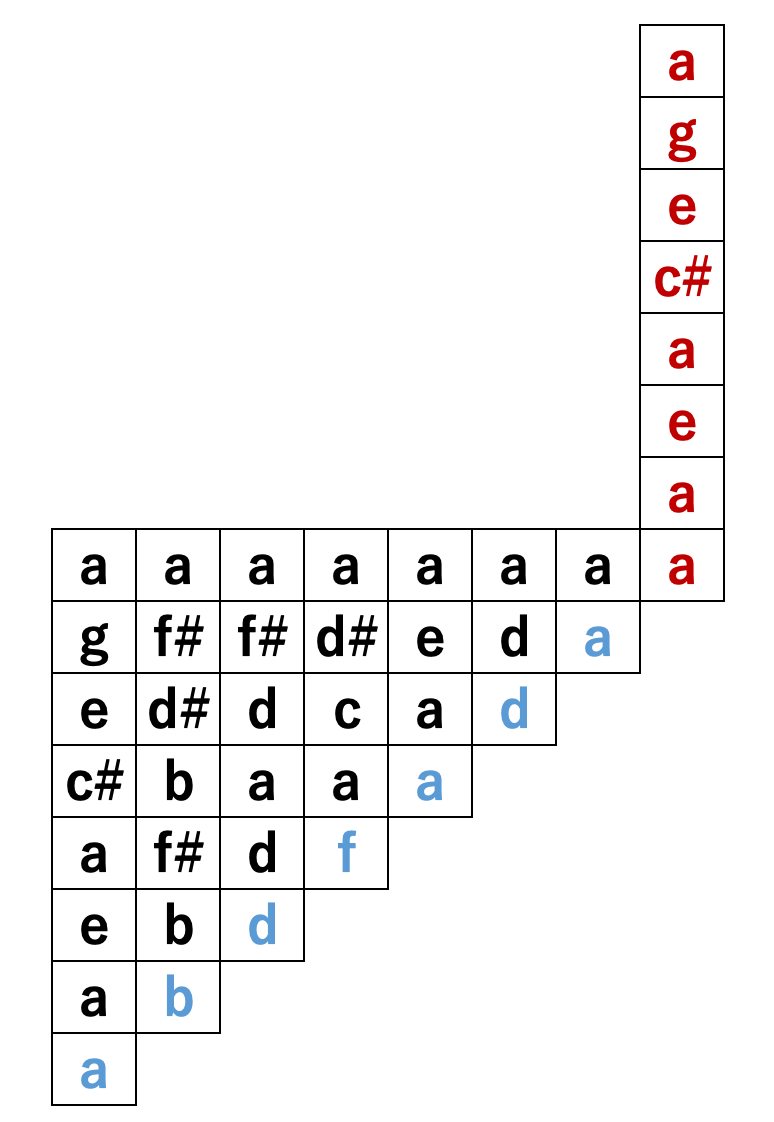
a音を弾く時、a音が生まれる世界(上方領域)、a音を生む世界(下方領域)が瞬時に仮想され、aを次に繋げたい、という動きへの生命の性質?から、次の音に、次の事象に繋げる作業が人間の本質である、と考えてみると、倍音世界が形作る傾きは、人が音楽を行う欲求が展開する傾きを持っている、と言ってもいいのではないでしょうか。
このひとくくりの外縁構造は、上方倍音だけでは不完全なのではないか、と思うのです。
当ブログ音楽理論関連記事目次はこちら
*1:
不定調性論では、倍音列(上方・下方)を音高そのものではなく、音の連関構造として扱います。
これは、群論的に音程関係を再定義するための試みでもあります。
倍音列において、各音高 は、基音 に対する整数乗として表現されます。
このとき、倍音列全体は乗法群(自然数乗)として記述可能です:
また、逆に下方倍音列はその逆数群と見なせるため:
この双方向性を視覚化し、抽象的に展開することで、音楽的連関を一種の数理的対称空間として捉えることが可能になります。
この空間では、音の高さはもはや主たる情報ではなく、連鎖・階層・相互関係の位置情報として扱われます。
したがって、和音や旋律は「空間内の経路」や「関数的な振る舞い」として描かれることになります。