かつらは時代遅れ。Amazonで爆売れ！少しでも髪あればOK
PR(株式会社ソーシャルテック)
立体の体積を求める問題は、公式を忘れてしまうと急に難しく感じることがあります。
とくに四角錐の体積は、日常ではあまり触れないため思い出しにくいかもしれません。
今回は、四角錐の体積をどのように求めるかを確認していきます。
問題
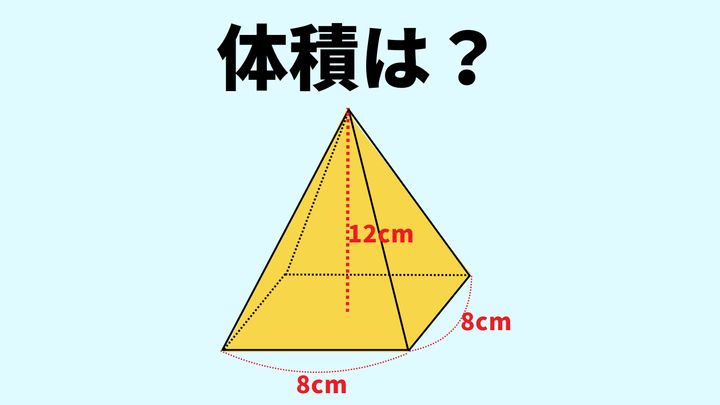
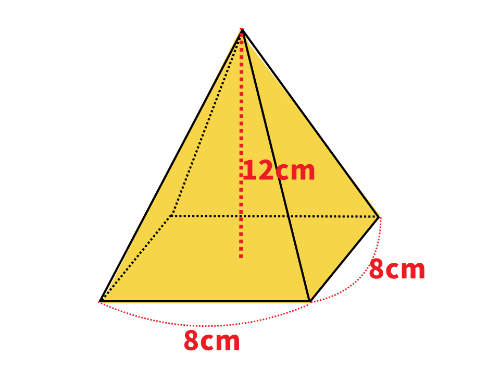
次の四角錐の体積を求めなさい。
（底面1辺8cmの正方形、高さ12cmの四角錐）
正しく求めることができるか、挑戦してみましょう。
解説
今回の問題の答えは「256(cm3)」です。
どのように計算するのか順に見ていきましょう。
四角錐の体積は次の公式で求められます。
四角錐の体積=底面積×高さ×1/3
まず、底面が正方形なので面積を求めます。
底面積（一辺8cmの正方形）
=8×8
=64(cm2)
次に、この底面積を公式に代入します。
四角錐の体積
=64×12×1/3
=64×4
=256(cm3)
以上より、求める体積は「256(cm3)」となります。
四角錐の体積について
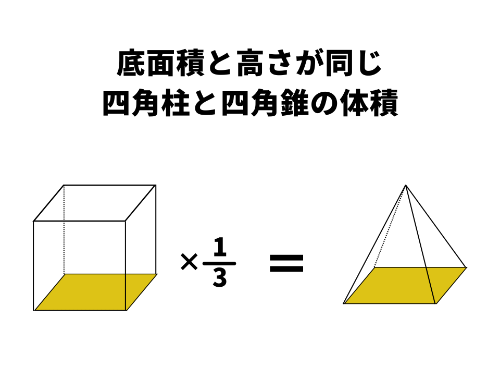
錐体（四角錐・三角錐・円錐など）の体積は、底面積と高さが同じ柱体の1/3になるという特徴があります。
そのため、どのような錐体でも必ず公式に1/3が含まれています。
まとめ
四角錐の体積は、「底面積×高さ×1/3」の公式に当てはめるだけで求めることができます。
底面の形が何であっても、考え方は共通です。ぜひ他の立体の問題にも挑戦してみましょう。
※当メディアでご紹介する数学関連記事においては、複数の解法を持つものもございます。
あくまでも一例のご紹介に留まることを、ご了承ください。
文（編集）：SAJIMA
日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」
スピード勝負！他の問題にも挑戦しよう！
