「手がかゆすぎる…」それ実はもう手遅れかも。たった1日10秒の裏技！
PR(さくらフォレスト株式会社)
算数や数学で学ぶ公式は、しばらく使わないと忘れてしまうことがあります。
特に円やおうぎ形に関する計算は、久しぶりに見ると戸惑ってしまう人も多いでしょう。
今回は、おうぎ形の弧の長さを求める基本的な問題に挑戦してみます。
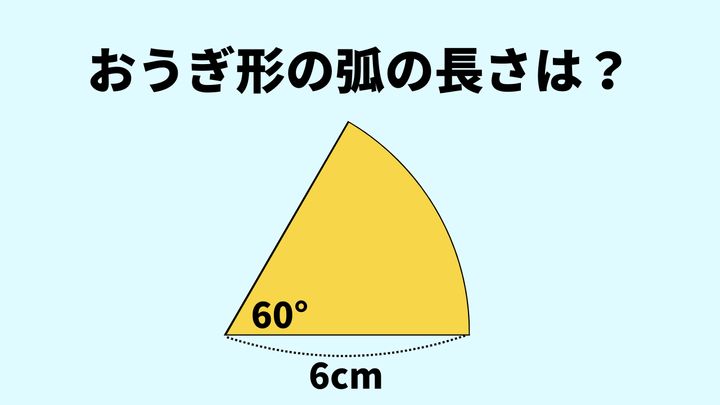
問題
半径6cm、中心角60°のおうぎ形の弧の長さを求めなさい。（円周率は3.14とする）
どのように考えれば、弧の長さを求めることができるでしょうか。
解説
今回の答えは「6.28cm」です。
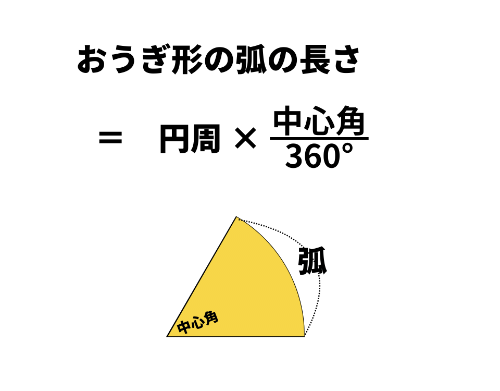
弧の長さは、円周の一部分にあたるため、次の考え方で求めることができます。
弧の長さ＝円周×中心角の割合
（中心角の割合は、「中心角/360°」で表す）
まず、半径6cmの円の円周を求めます。
円周
=直径×円周率
=12×3.14
=37.68(cm)
次に、中心角60°が円全体（360°）の何倍にあたるかを考えます。
60÷360=1/6
したがって、弧の長さは次のように計算できます。
弧の長さ
=37.68×1/6
=6.28(cm)
これが求める弧の長さです。
おうぎ形の弧の長さについて
おうぎ形は「円の一部分」です。
そのため、中心角が360°のときは円周すべて、180°なら半分、90°なら4分の1というように、中心角の割合を使って弧の長さが決まります。
今回の問題は、中心角が60°なので、円周の6分の1の長さになります。
まとめ
おうぎ形の弧の長さは、「円周を求める→中心角の割合をかける」という流れで計算できます。
円の基本公式を思い出しながら取り組むことで、円周や面積の問題にも応用しやすくなります。
ぜひ他のおうぎ形の問題にも挑戦してみてください。
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。
あくまでも一例のご紹介に留まることを、ご了承ください。
文（編集）：SAJIMA
日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」
スピード勝負！他の問題にも挑戦しよう！
