多角形の内角の和の求め方、今でも覚えているでしょうか?
公式を忘れてしまっても、「内角の和を求めるための考え方」さえ思いつけば、自力で式を立てられますよ。
今回は、七角形の内角の和を求めてみましょう。
問題
七角形の内角の和を求めなさい。
ヒント:七角形を「ある形」に分割して考えることです。頭の中で、七角形に補助線を引いてみましょう。
解答
正解は、「900°」です。
どのように計算をすればよいのか、分かりましたか?
次の「ポイント」では、図を用いて今回の問題の計算方法を解説しています。ぜひ、ご覧ください。
ポイント
この問題のポイントは、「七角形を三角形に分割して考えること」です。
まず前提として、「三角形の内角の和は必ず180°になる」ことを押さえておきましょう。この知識を使って、七角形の内角の和を求めていきます。
補助線を引いて、七角形を三角形に分割する方法は二つあります。
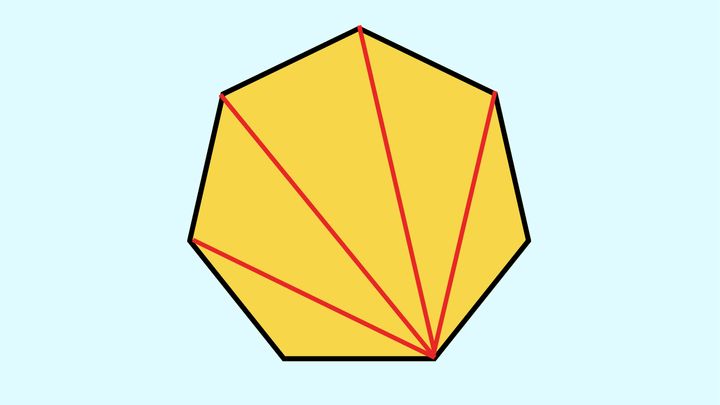
【その1】三角形5個に分割する
以下の図のように七角形の一つの頂点から他の頂点に向かって補助線を引くと、三角形が5個できます。
こうしてできた三角形の角は、すべて元の七角形の内角を含んでいます。よって、三角形5個の内角の和と七角形の内角の和は一致します。
180°×5=900°
三角形の内角の和は180°ですから、それを5倍すれば、七角形の内角の和になるのです。
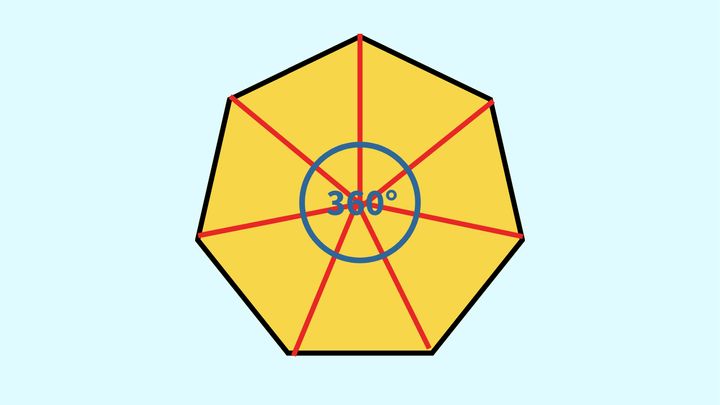
【その2】三角形7個に分割する
以下の図のように、七角形の頂点から内側の一点に向かって補助線を引いていくと、三角形が7個できます。
ただし、中央に集まる三角形の角は、七角形の内角からできたものではありません。また、中央に集まる三角形の角の合計は上の図のように全部で360°になります。
よって、七角形の内角の和を求めるには、まず7個の三角形の内角の和を求め、次に360°を引けばよいのです。
180°×7=1260°
1260°−360°=900°
三角形の内角の和は180°ですから、これを7倍して三角形7個の内角の和を求めます。その答えから360°を引くと、七角形の内角の和が算出されます。
答えは、「三角形を5個に分割したとき」と一致しますね。
まとめ
n角形の内角の和は、次の公式で求められます。
n角形の内角の和
180°×(n−2)
この公式の背景には、「補助線で多角形を三角形に分割する」という今回の問題で紹介した考え方があります。公式を暗記していなくても、三角形をベースにした計算方法を理解していれば、多角形の内角の和を求めることができるでしょう。
学生時代に習った公式は大人になると忘れてしまいがちです。そんなときは、公式に頼らず自力で解法を見つけるのも楽しいものです。頭の体操のつもりで、他の問題にもチャレンジしてみてくださいね。
※当メディアでご紹介する数学関連記事において、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。
文(編集):VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。
スピード勝負!他の問題にも挑戦しよう!