二値分類タスクにおける特徴量選択のアプローチとしてのKolmogorov-Smirnov検定
はじめに
二値分類タスクにおいて「結局どの特徴量が重要なの?」――この問いに悩んだ経験、ありませんか?
特徴量が多ければモデルは柔軟になります。しかし同時に、次のような課題が発生します。
- 計算負荷の増大
- 解釈性の低下
- 保守性の低下
これらの問題は特にエッジ実装(自動車ECUやIoT機器等)で顕著です。リアルタイム処理やメモリ制約が厳しい環境では、少数の特徴量で高い精度を出す工夫が求められます。
本記事では、二値分類タスクでの特徴量選択の第一歩として、Kolmogorov-Smirnov検定(KS検定)の統計量を特徴量の重要度を示す定量的評価指標として活用するアプローチを紹介します!
さらに、公開データセットを使った実証実験と、他手法(Feature Importance・SHAP)との比較を通じて、その有効性を確認します。
特徴量選択にKS検定の統計量を用いる場合の優位性
具体的な説明に入る前にまず、これから紹介する手法の優位性を列挙します。
- モデル学習前に特徴量を評価可能
-
モデル非依存(ノンパラメトリック検定)・軽量
- KS検定の統計量は計算が速いため、特徴量のスクリーニングに適する。
-
クラス間のデータ数が異なっても利用可能
- 実務データではクラス間のデータ数の用意難易度が異なることが多い。
-
“理想的な特徴量”の検知
- クラス間の分布が完全に分離している特徴量を、KS統計量が 1 として検知できます。
- もしそんな特徴量が見つかれば、複雑なモデルは不要。
- 閾値ひとつで、統計量計算に用いたデータについては完全に分類できます。
- ※リークや妥当性の検証は必須
実務に役立つ多くの優位性を持つため、モデル構築に有効な特徴量を短時間で簡単に選択することができます!
Kolmogorov-Smirnov検定とは
Kolmogorov-Smirnov検定(KS検定)とは、2つの分布に“差があるか”を調べるための統計的手法です。
- 帰無仮説:「2つの分布は同じ」
- 検定統計量:累積分布関数 (CDF) の最大差
- p値:差が偶然起きる確率
今回はp値ではなく統計量そのものに注目します!
KS検定の統計量の説明 (なぜ特徴量選択に使えるのか)
二値分類(クラス0/クラス1を分類)に有効な特徴量とは、クラス0とクラス1の分布が大きく異なる特徴量です。K–S統計量
KS検定の統計量
計算式で見てもイメージしにくいので以下に図解します。
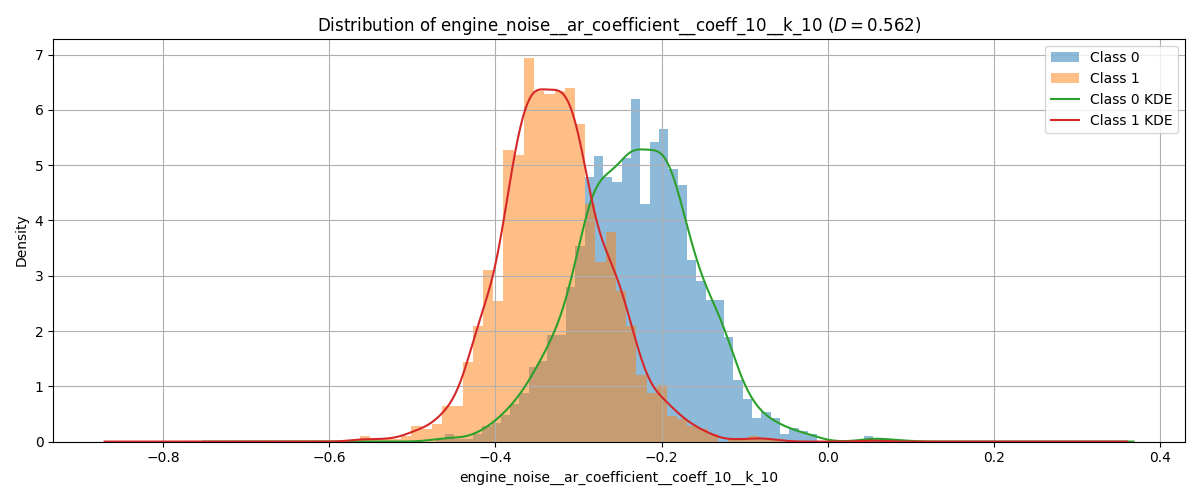
この後の実証実験で使用する特徴量の一例についての目的変数別の分布を以下の図1, 2に示します。
図1. クラス0 / クラス1 の分布例 (ヒストグラム + KDE)
これらを累積分布関数に変換したものが以下に示す図2です。
図2. クラス0 / クラス1の累積分布関数とKS統計量
各クラスの累積分布関数の差の最大値(赤線で表示)がKS統計量
クラス間の分布が異なるほど、その特徴量で二値分類しやすいというのは直感的にも納得できますよね!
この分布の差の定量的な評価指標としてKS統計量
今回紹介するアプローチ
『自動特徴量生成 × KS統計量で定量的評価』
少数の重要な特徴量で二値分類をするために、“特徴量を増やす” → “重要なものに絞る”という戦略を取ります。
ここで利用するのが、『自動特徴量生成モジュール』 と 『KS統計量による重要度ランキングを用いた特徴量選択』です。
本手法を含めたデータ分析の流れの全体像
データ準備 → 前処理 → 特徴量生成 → KS統計量を用いた特徴量選択 → モデル学習/評価
-
特徴量生成
機械学習の精度を左右するのはデータ量と特徴量の質。
今では便利なことに、自動で大量の特徴量を生成してくれるfeaturetoolsやtsfreshといったモジュールがあります。
まずはこれを利用して特徴量を生成しましょう。(本記事ではtsfreshを利用) -
KS統計量を用いた特徴量選択
全特徴量について、それぞれクラス0とクラス1の分布の差についてKS統計量
-
-
この時点でモデル学習をするまでもなく完璧な二値分類が可能です!(※その特徴量の妥当性・リークの有無は要確認)
-
-
モデル学習/評価
ランキング上位の特徴量から学習に用いる特徴量を選んでいくことで、少数の重要な特徴量に絞って学習/評価できます。
(本記事ではモデルにランダムフォレストを利用)
この後の実証実験では前処理済みの公開データセットを用いて、特徴量生成からモデル学習/評価までを行います。
実証実験
公開データセットであるFordAを用いて、tsfresh × KS統計量ランキングで特徴量選択の効果を確認する。
データについて
実証実験にはFordAデータセット (UCR/UEA Time Series Archive) を利用します。
これは、エンジンノイズのセンサーデータから故障の有無を分類するタスクのための公開データセットであり、次のリンクからダウンロードできます。
Welcome to the UCR Time Series Classification/Clustering Page
概要:
- タスク:二値分類 (正常 / 異常)
- サンプル数:4921 (Train: 3601, Test: 1320)
- 各サンプルは長さ500の時系列データ
- 次元数:1 (単変量時系列)
- 前処理済み
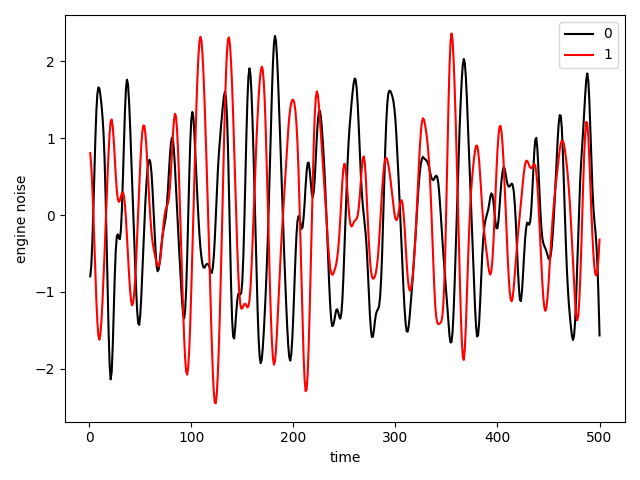
図3. 各クラスのデータ例 (黒:正常, 赤:異常)
図3は各クラスから1つずつデータをプロットしたものです。各データはこの1つの特徴量だけを持つため、このままでは分類が難しい。
特徴量生成
今回は時系列データから簡単に大量の特徴量を生成できるtsfreshを利用して特徴量を生成します。
生成される特徴量は、平均・分散・歪度・ピーク数・FFT係数など多岐にわたります。
コード(データ読込 → 整形 → 特徴量生成)
import numpy as np
import pandas as pd
from pathlib import Path
from tsfresh import extract_features, select_features
from tsfresh.utilities.dataframe_functions import impute
# tsfreshを用いるためのデータ整形
def df_shaping(raw_df: pd.DataFrame, first_data_id: int = 0) -> pd.DataFrame:
n_time = raw_df.shape[1] - 1
shaped = raw_df.copy()
shaped.columns = ["target"] + list(range(n_time))
shaped["data_id"] = np.arange(first_data_id, first_data_id + len(shaped))
df = shaped.melt(id_vars=["data_id", "target"], var_name="time", value_name="engine_noise")
df = df.sort_values(["data_id", "time"]).reset_index(drop=True)
return df
# データの読み込み
raw_train_df = pd.read_csv("FordA/FordA_TRAIN.tsv", sep="\t", header=None)
raw_test_df = pd.read_csv("FordA/FordA_TEST.tsv", sep="\t", header=None)
train_df = df_shaping(raw_train_df)
test_df = df_shaping(raw_test_df, first_data_id=(train_df["data_id"].max() + 1))
# 特徴量生成共通化のため結合
all_df = pd.concat([train_df, test_df], ignore_index=True)
# tsfreshによる特徴量生成
all_fe_df = extract_features(
all_df.copy()[["data_id", "time", "engine_noise"]], column_id="data_id", column_sort="time"
)
# tsfreshによる特徴量選択
impute(all_fe_df)
all_id_target = pd.concat([raw_train_df.iloc[:, 0], raw_test_df.iloc[:, 0]], ignore_index=True).rename("target")
all_fe_filt_df = select_features(all_fe_df, all_id_target)
print("shape", all_fe_filt_df.shape)
# 生成した特徴量と目的変数をconcatして一つのデータセットに
all_dataset = pd.concat([all_fe_filt_df, all_id_target], axis=1)
# train, testの再分割
n_train = len(raw_train_df)
train_dataset = all_dataset.copy().iloc[:n_train, :]
test_dataset = all_dataset.copy().iloc[n_train:, :]
tsfreshを用いることで、FordAの1つの特徴量から247個まで特徴量を増やすことができました!
KS統計量による特徴量の重要度ランキング作成
生成した特徴量ごとに、クラス0(正常)とクラス1(異常)の値を比較し、
二標本K–S統計量
コード(KS統計量ランキング作成)
from tqdm import tqdm
from scipy.stats import ks_2samp
from matplotlib import pyplot as plt
def ks_score(feature: pd.Series, target: pd.Series) -> float:
"""
各特徴量に対して、クラス0とクラス1の分布差をKS統計量で算出。
NaNは除外。
"""
# NaN除去
data = pd.DataFrame({"feature": feature, "target": target}).dropna()
x0 = data.loc[data["target"] == -1, "feature"]
x1 = data.loc[data["target"] == 1, "feature"]
# 両方のクラスに十分なサンプルがない場合はスキップ
if len(x0) < 10 or len(x1) < 10:
return np.nan
# KS検定
ks_stat, _ = ks_2samp(x0, x1)
return ks_stat
def compute_ks_for_all_features(df: pd.DataFrame, target_col: str = "target") -> pd.DataFrame:
"""
DataFrame中の全ての数値特徴量についてKSスコアを計算し、
スコア順に並べたDataFrameを返す。
"""
target = df[target_col]
features = [col for col in df.columns if col != target_col and np.issubdtype(df[col].dtype, np.number)]
results = []
for f in tqdm(features, desc="Computing KS statistics"):
try:
ks_value = ks_score(df[f], target)
results.append((f, ks_value))
except Exception as e:
print(f"[WARN] Feature {f} skipped due to error: {e}")
ks_df = pd.DataFrame(results, columns=["feature", "ks_stat"]).dropna()
ks_df = ks_df.sort_values(by="ks_stat", ascending=False).reset_index(drop=True)
return ks_df
def plot_ks_ranking(ks_df, rank_num=15):
ks_df_for_plot = ks_df.copy().iloc[:rank_num, :]
ks_df_for_plot = ks_df_for_plot[::-1]
plt.figure(figsize=(8, 5))
plt.rcParams["font.family"] = "sans-serif"
plt.xlabel("ks_stat")
plt.title(f"K-S Ranking Top{rank_num}")
plt.barh(ks_df_for_plot["feature"][:], ks_df_for_plot["ks_stat"][:], color="skyblue")
# 各バーに数値を表示
for index, value in enumerate(ks_df_for_plot["ks_stat"]):
plt.text(value - 0.15, index, f"{value:.2f}", va="center")
plt.tight_layout()
plt.show()
plt.clf()
plt.close()
ks_train_df = compute_ks_for_all_features(train_dataset)
plot_ks_ranking(ks_train_df)
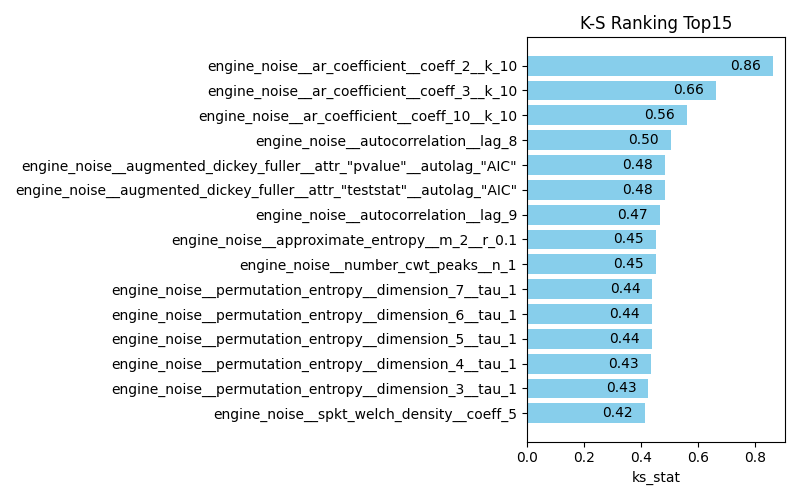
このコードで算出したKS統計量によるランキングが以下の図4です。
図4. KS統計量による重要度ランキング (Top15)
ランキングを見ると、
これらはクラス間で分布が完全に分離しているため、もしこの特徴量が妥当でリークもないと確認できれば、モデルの学習をするまでもなくその特徴量だけで分類可能!
…ですが、現実はそう甘くはありません。
実務データでこんな“理想的な特徴量”が見つかることは稀です。
多くの場合は有効な特徴量をいくつか組み合わせてモデル化する必要があります。
以降ではランキング上位5つの特徴量はなかったということにして、モデルの学習 / 評価、他手法との比較を行います。
特徴量選択のための重要度の指標としてKS統計量が有効であることを確認していきます!
※以降のセクションでは、精度が簡単に出てしまうことで比較が難しくなるのを避けるため、図4のランキング上位5つの特徴量を一切使いません。
以降も「上位何個を選択」等書きますが、これは上位5つを除いた上でのランキングを示します。
モデル学習 / 評価
KS統計量による特徴量選択が有効であることを、全特徴量で学習したモデルと特徴量を厳選(上位10個)したモデルの精度比較により確認します。
今回使用するモデルは次のようなランダムフォレストです。
使用モデル:
from sklearn.ensemble import RandomForestClassifier
rf_model = RandomForestClassifier(
n_estimators=5, # 木の本数(少なめ)
max_depth=5, # 木の深さ(浅め)
random_state=42 # 再現性確保
)
深いモデルや大量の木を使えば精度は上がりますが、解釈性が下がり、軽量化の意義が薄れるため、あえて浅いモデルで「特徴量選択の効果」確認します。
K–S統計量ランキングによる特徴量選択の有効性を確認するため、学習に用いる特徴量を次の条件で選択しテストデータで評価しました。
- 全特徴量(242個)
- ランキング上位10個の特徴量
精度比較
| 使用特徴量 | 特徴量数 | Accuracy | Precision | Recall | F1-score |
|---|---|---|---|---|---|
| 全特徴量 | 242 | 0.9447 | 0.9449 | 0.9453 | 0.9447 |
| K–S上位10特徴量 | 10 | 0.9591 | 0.9590 | 0.9591 | 0.9591 |
実験結果に対する考察
特徴量を約96%削減したにもかかわらず、精度を保つどころか向上しています!
これはK–S統計量による特徴量選択がノイズを減らし、モデルの汎化性能を高めたためであると考えられます。
実務での価値:
- 精度 → 汎化性能の向上による精度向上
- 軽量化 → 学習/推論速度・メモリ効率の向上
- 解釈性 → 特徴量の数が10個程度ならモデル解釈も現実的
他の手法との比較
今回紹介したKS統計量ベースの特徴量重要度ランキングがどれくらい有効なのか、一般的に特徴量の重要度ランキングに使われる手法と比較を行いました。
比較対象手法
- Feature Importance (FI)
- SHAP (SHapley Additive exPlanations)
これらは簡単に言うと、モデルに一度学習させてから、そのモデルの予測にどの特徴量がどれだけ寄与しているかを算出したようなものです。詳しく知りたい方は、こちらの記事がとても参考になります。「特徴量重要度」について少しだけ真剣に考えてみる
以下に比較対象のそれぞれのランキングを示します。今回のFIとSHAPのランキング作成には前節で用いた全特徴量で学習したモデルを使用しました。
図5. KS統計量による重要度ランキング (Top15) (図4からモデル学習に使わない5特徴量を除いたもの)
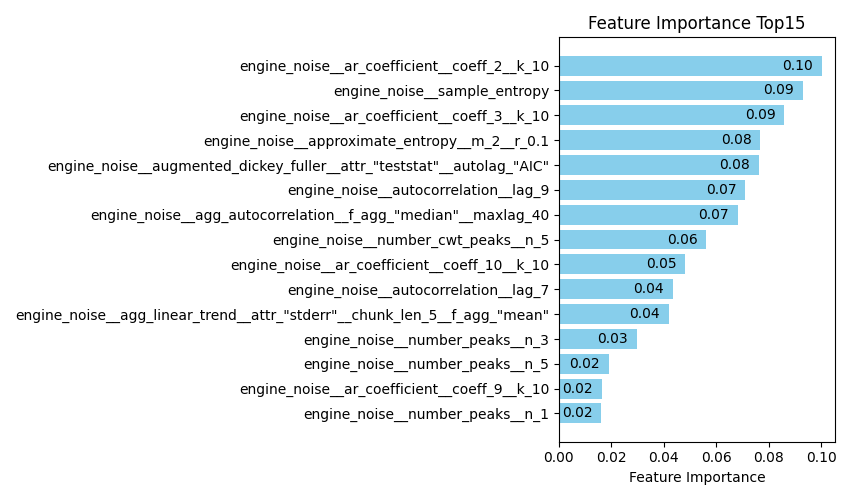
図6. Feature Importanceによる重要度ランキング (Top15)
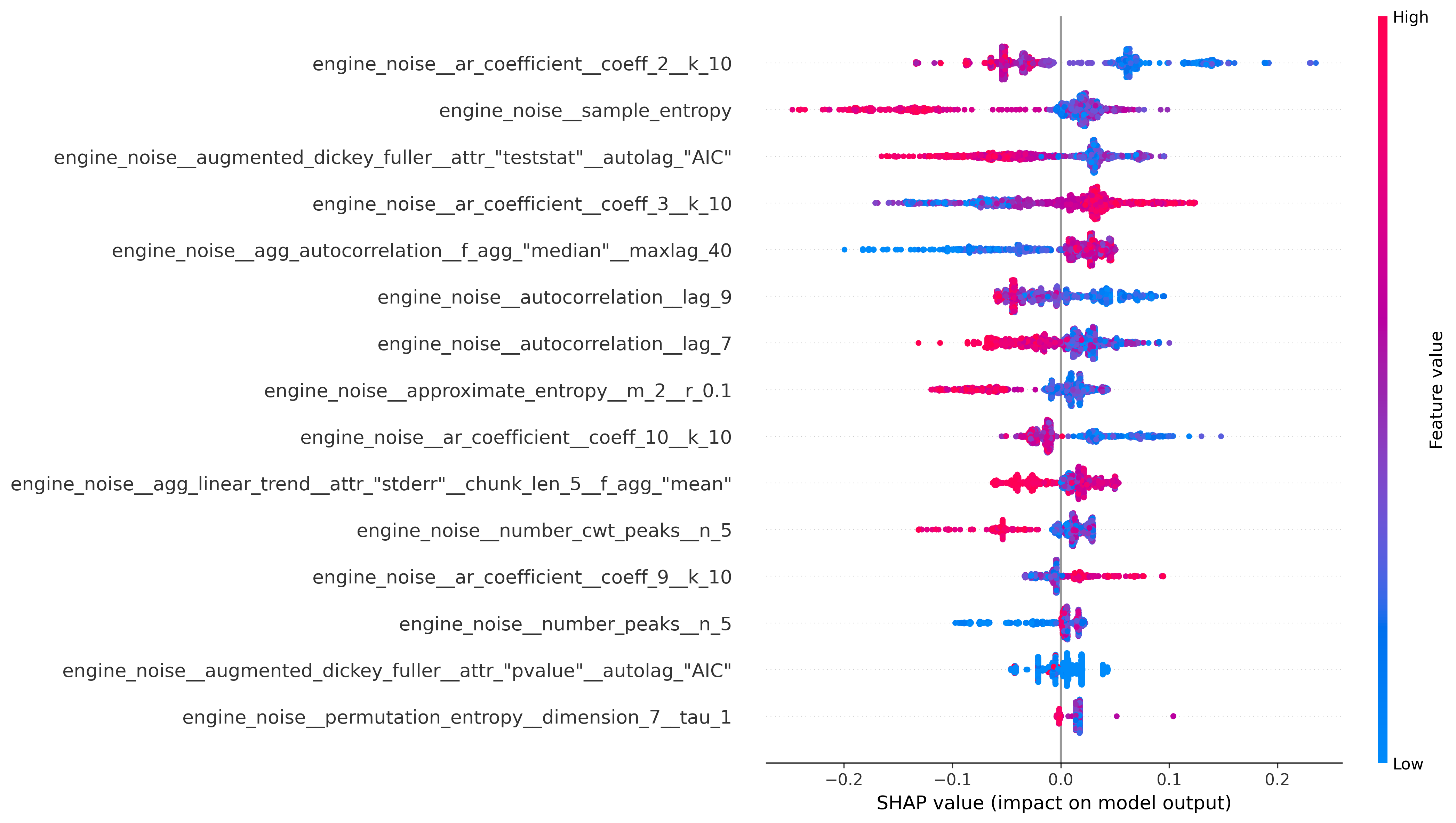
図7. SHAPによる重要度ランキング (Top15) (shap.summary_plot)
ここから、これらのランキングを用いて2パターンの比較を行います。
比較概要
-
パターン1:1つの特徴量だけを用いて学習したモデルの精度をそれぞれのランキング順に比較 -
パターン2:学習に用いる特徴量の数をそれぞれのランキング順に増やしながら精度を比較
比較条件
- 使用モデル:前節と同様のランダムフォレスト
- 精度評価指標:Accuracy, Precision, Recall, F1-score
- プロットの各点:その点の条件の特徴量を用いて学習したときの精度
- 特徴量選択に用いるランキングだけが異なる
比較1:1つの特徴量で学習したモデルの精度
特徴量1つで学習したモデルの精度が、その特徴量単独で持つ分類力であると考え、各特徴量についてそれぞれ1つずつ用いて学習/精度評価を行いました。それをそれぞれのランキング順にプロットしたものを以下に示します。
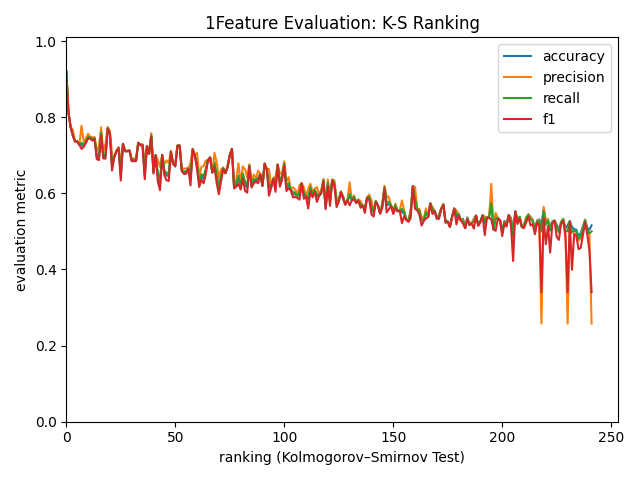
図8. 1特徴量で学習したモデル精度 (KS Ranking順) (横軸:使用特徴量のランキング順位, 縦軸:精度)
KSランキングでは精度と順位がほぼ対応しており、上位特徴量がモデル性能に直結する傾向が確認できます!
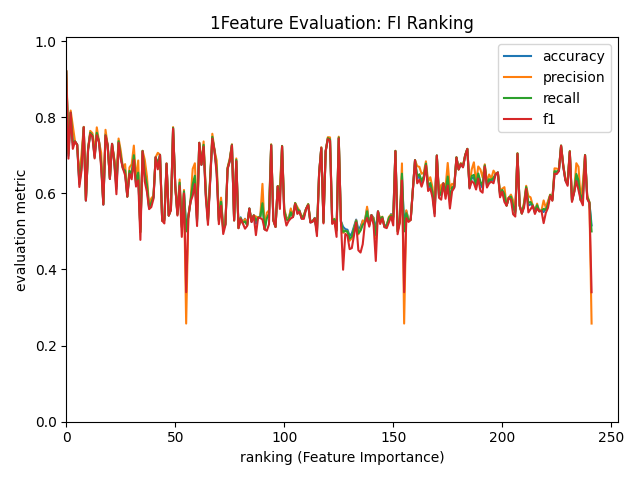
図9. 1特徴量で学習したモデル精度 (FI Ranking順) (横軸:使用特徴量のランキング順位, 縦軸:精度)
図10. 1特徴量で学習したモデル精度 (SHAP Ranking順) (横軸:使用特徴量のランキング順位, 縦軸:精度)
一方、FIとSHAPでは順位と精度の対応が不安定に見えます。
このように、KS統計量を用いた方がより直感に合った有効な特徴量のランク付けができているように見えます!
比較2: 特徴量をランキング順に増やしていったときのモデル精度推移
次に、学習に使用する特徴量をランキング順に増やしていった時のモデル精度の推移を比較しました。
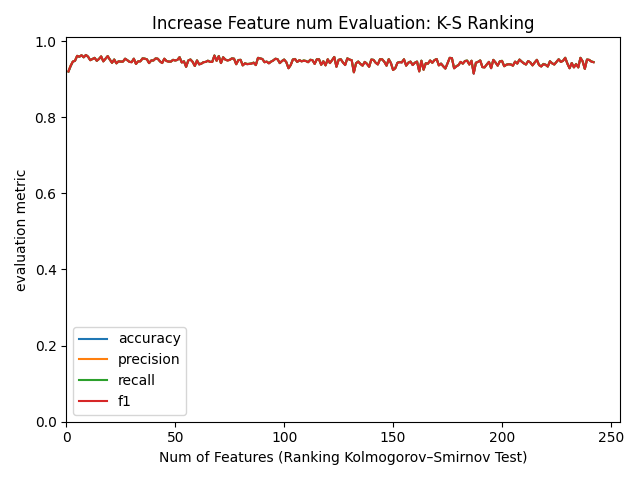
図11. 特徴量数をランキング順に増やしたときのモデル精度推移 (KS Ranking順) (横軸:特徴量数, 縦軸:精度)
図12. 特徴量数をランキング順に増やしたときのモデル精度推移 (FI Ranking順) (横軸:特徴量数, 縦軸:精度)
図13. 特徴量数をランキング順に増やしたときのモデル精度推移 (SHAP Ranking順) (横軸:特徴量数, 縦軸:精度)
いずれのランキングにおいても最初の10個程度の特徴量を用いた時点で精度が飽和していることが確認できます!これは特徴量は多ければ良いというものでもなく、少数の重要な特徴量だけで十分であることが示唆されます。
また、特徴量数の少ない一部領域を拡大して、それぞれのAccuracyを比較してみると、
図14. 各手法のAccuracy比較 (一部領域拡大)
若干KSランキングの結果が、立ち上がりが早いようにも見えます。
モデル学習前に素早く確認できるKSランキングで他手法と同等かそれ以上の結果を得られることから、この手法を試す価値は十分にあると考えられます!
このように、KS統計量によるランキングの上位から特徴量を選んでいくことで、有効な特徴量を効率的に選択することができます。
さらに、FIやSHAPのランキングを作成するには一度モデルに学習させる必要があり、結果もモデル依存であるのに対し、KS統計量によるランキングはモデル学習前に、素早く、モデル非依存なランキングを作成できます!
注意点:
ここで、KS統計量による特徴量の重要度評価の限界と他手法との違いについて触れておきます。
KS統計量は各特徴量を単独で評価し、クラスごとの分布差を測る指標です。そのため、特徴量同士の相互作用までは考慮できません。
比較まとめ表
| 特徴量の重要度指標 | モデル依存性 | 計算コスト | 相互作用考慮 | 解釈性 | 学習前評価 |
|---|---|---|---|---|---|
| KS統計量 | なし | 低 | なし | 高(分布差を図示可能・直感的) | ✅ |
| Feature Importance | あり | 中 | 部分的 | 中(モデル構造依存) | ❌ |
| SHAP | あり | 高 | あり | 高(局所・大域両方を説明可能) | ❌ |
このように、KS統計量は相互作用を評価できないという制約がありますが、モデル非依存・軽量・学習前に使える・直感的に説明しやすいという強みは、探索の第一ステップとして非常に価値があります!
まとめ
二値分類タスクで「どの特徴量が重要なのか」を素早く見極めたい――そんな場面で、Kolmogorov–Smirnov(K-S)統計量を使った特徴量選択は有力な選択肢です。
今回紹介したポイント:
- KS統計量の役割:クラス間の分布差の定量的評価指標
- 特徴量選択への活用:モデル学習前に、軽量・モデル非依存でランキングを作成可能
-
“理想的な特徴量”の検知:
- 実証結果:少数の特徴量で精度を維持、むしろ向上するケースもあり
- 比較で見えた強み:FIやSHAPに比べ、KSは「速い」「直感的」「学習前に使える」
- 実務でのメリット:開発初期に「重要な特徴量」を見極めることで、効率的なモデリングが可能
二値分類タスクにおける特徴量の重要度の定量的評価指標として、KS統計量はシンプルで強力な武器です。
ぜひ、あなたのプロジェクトでも試してみてください!
最後まで読んでいただきありがとうございました!
本記事の内容に誤りなどあればコメントにてご教授お願いいたします。



Comments
Let's comment your feelings that are more than good