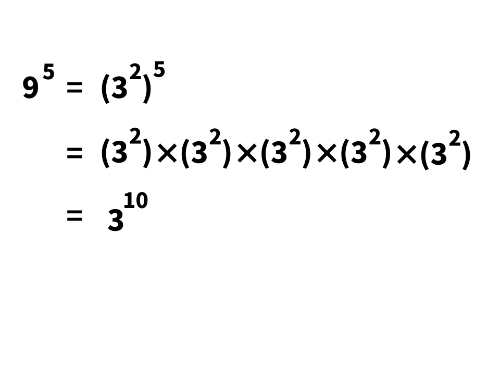1日たった10秒でできる水虫治療法とは？水虫の人絶対やって
PR(株式会社アルトルイズム)
「累乗」を使うと、大きな数でもコンパクトに表すことができます。
しかし、指数の扱い方を正しく理解していないと、計算で戸惑ってしまうことがあります。
今回は、累乗の性質を使って計算する問題に挑戦してみましょう。
問題
次の計算をしなさい。
(9^5)÷(3^7)
※当メディアでは、「9の5乗」のような累乗を「9^5」と表します。
「9^5」をそのまま計算すると非常に大きな値になりますが、指数の性質を使うと素早く簡単に解くことができます。
解説
今回の問題の答えは「27」（3の3乗）です。
途中の計算は次のようになります。
(9^5)÷(3^7)
=(3^10)÷(3^7)
=3^3
=27
どのように計算をしたのか解説をしていきます。
まず「9^5」を簡単になるように変形します。
9=3^2 なので、
9^5=(3^2)^5=3^10
となります。
この計算をまとめると、次のようになります。
よって、元の式は次のように変形できます。
(3^10)÷(3^7)
「3を10回掛け算した数」を「3を7回掛け算した数」で割るので、その計算結果は「3を3回掛け算した数」になります（10−7=3）。
したがって、
3^3=27
よって、答えは「27」です。
まとめ
指数の計算は、数が大きくなると地道な計算が難しくなります。
そのため、累乗の仕組みを理解して、工夫した計算が必要です。
忘れていた方は、この機会にぜひ整理してみてください。
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。
あくまでも一例のご紹介に留まることを、ご了承ください。
文（編集）：SAJIMA
日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」
スピード勝負！他の問題にも挑戦しよう！
