「手がかゆすぎる…」それ実はもう手遅れかも。たった1日10秒の裏技！
PR(さくらフォレスト株式会社)
さまざまな立体を組み合わせることで、複雑に見える形の体積も求められるようになります。
一見難しそうな立体でも、基本となる形に分ければ落ち着いて計算できます。
今回は、中心に穴が開いた立体の体積を求める問題に挑戦してみましょう。
問題
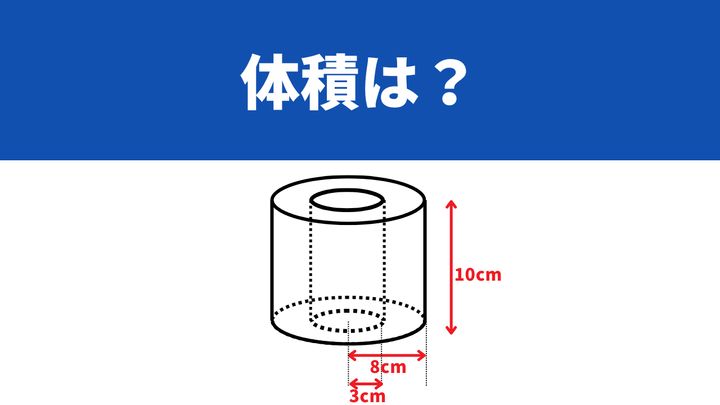
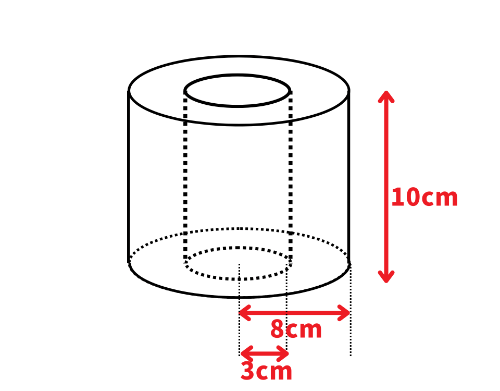
次の立体の体積を求めなさい（円周率は3.14とする）。
中心に穴が開いた円柱のような形をしています。
どのようにして体積を求めればよいでしょうか。
解説
今回の問題の答えは「1727(cm3)」です。
どのように求めるのか順に確認していきます。
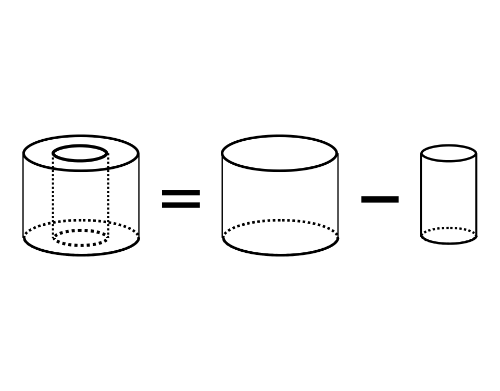
この立体は、外側に大きな円柱があり、その中心部分が小さな円柱としてくり抜かれています。
つまり、外側の円柱の体積から、内側の円柱の体積を引けばよいことになります。
円柱の体積は次の公式で求められます。
円柱の体積=底面積×高さ
今回の立体の情報は次の通りです。
外側の円柱
半径8cm、高さ10cm
内側の円柱
半径3cm、高さ10cm
では、底面積を計算していきます。
＜外側の円柱の底面積＞
8×8×3.14
=200.96(cm2)
＜内側の円柱の底面積＞
3×3×3.14
=28.26(cm2)
次に、体積を求めます。
求める体積
=(200.96×10)−(28.26×10)
=2009.6−282.6
= 1727(cm3)
小数の計算を含むため、途中の計算は注意が必要です。
上記では式を分割して計算をしましたが、以下のように計算すると少し簡単になります。
（別解・計算の工夫）
求める体積
(8×8×3.14×10)−(3×3×3.14×10)
=(640×3.14)−(90×3.14)
=(640−90)×3.14
=550×3.14
=1727(cm3)
ここでは分配法則を利用して「×3.14」の計算を一回にまとめています。これによって、途中で小数の計算が不要になりますね
以上より、この立体の体積は「1727(cm3)」となります。
まとめ
今回のような「くり抜かれた立体」は、外側の体積から内側の体積を引くことで求められます。
複雑に見えても、基本的な形に分解すれば確実に計算できます。
計算の工夫を取り入れることで、より効率よく求めることができました。
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。
あくまでも一例のご紹介に留まることを、ご了承ください。
文（編集）：SAJIMA
日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」
スピード勝負！他の問題にも挑戦しよう！
