泥っぽい便が出る…「歩き屁」増えたは、大腸SOS！気づいて。
PR(明治薬品株式会社)
今回は、小学生でも分かる「小数どうしの掛け算問題」にチャレンジしましょう。
しかし、計算ルールを習ったばかりの小学生には簡単でも、小数の計算が久々という大人にとってはかえって難しい問題かもしれません。
さて、あなたは正解できるでしょうか？
問題
次の計算をしなさい。
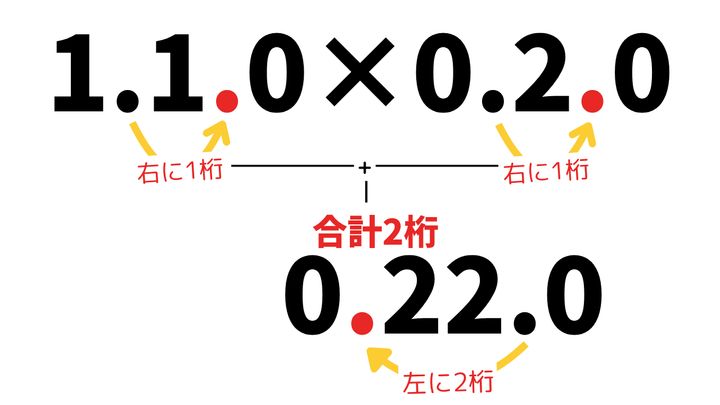
1.1×0.2
解答
正解は、「0.22」です。
22や2.2と答えてしまった人は、残念ながら不正解です。大事な小数点の位置が、ずれてしまっています。
では、この問題はどうやって計算すればよいのか、次の「ポイント」で確認しておきましょう。
ポイント
小数の掛け算のポイントは、「小数点の動き」です。
まずは、小数の掛け算のルールを思い出しましょう。
<小数の掛け算のルール>
ステップ1：小数の小数点を右に動かして整数の掛け算を作る
ステップ2：整数の掛け算をする
ステップ3：掛け算の答えの小数点をステップ1で右に動かした桁の合計分、左に動かす
では、さっそくこの三つのステップに沿って、今回の問題を計算してみましょう。
ステップ1：1.1×0.2を11×2にする（1.1→11、0.2→2としたので小数点は合計二桁分右に動いている）
ステップ2：11×2=22
ステップ3：22（22.0）の小数点を左に二桁分動かす→0.22が答えになる
小数点の動きさえ分かっていれば、計算自体はさほど難しくないはずです。
小数の移動方向を間違えないためのポイント
小数の掛け算では小数点を一度右へ動かして整数の掛け算を作ります。掛け算の後は、答えの小数点を今度は左へ動かします。
「右に行ったり、左に行ったり、ややこしくて小数点の動きを覚えられない」という人は、小数を掛けることの意味を考えてみましょう。
例えば、A×2はAを2倍する計算なので、答えは当然Aよりも大きくなります。しかし、A×0.2はAを0.2倍する計算なので、答えはAよりも小さくなります。
こう考えれば、1.1×0.2の答えは、11×2の答えよりも小さくなるはずです。答えを小さくするには、11×2の小数点を右ではなく左に動かす必要があると分かりますね。
小数点の動きの意味
小数点の動きの意味をもっと知りたいという人は、三つのステップを次のように式を変形している過程として考えてください。
1.1×0.2
=(11×1/10)×(2×1/10)←1.1は11×1/10、0.2は2×1/10のこと
=11×2×1/10×1/10←11×2を先に計算する
=22×1/10×1/10←1/10×1/10=1/100
=22×1/100
=22/100
=0.22
三つのステップを丸覚えするのが嫌だ、という人は、上のように式を変形していく流れを理解してください。自然と、小数の掛け算ができるようになりますよ。
まとめ
今回は、小数×小数の計算問題にチャレンジしました。
小数を含んだ掛け算は、一度整数の掛け算として計算してから、あとで小数点を移動します。小数点は整数にするときに一度右に動かし、答えを出すときに逆の左に動かします。
この小数点の移動がスムーズにできるようになれば、小数の掛け算に難しさを感じることはなくなるはずです。また計算方法を忘れないようにすためには、「どうしてこの方法で計算できるのか」を考えることも大事ですよ。
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。
文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。
スピード勝負！他の問題にも挑戦しよう！
