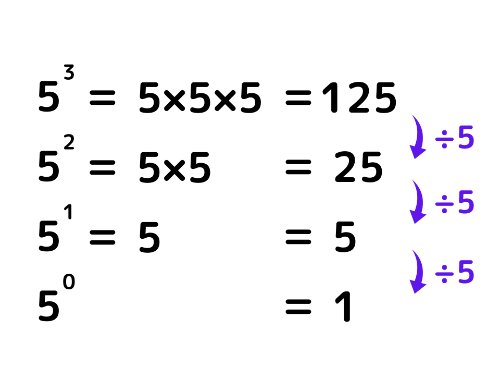大人が意外と解けない数学「5^0」→正しく計算できる？

何度も繰り返し掛け算をするときは、2乗、3乗など「累乗」を用いて表します。

では「0乗」の計算はどのようにすればいいのでしょうか。

「0回掛け算をする」というのは計算結果はどのようになるのか、正しく理解しているでしょうか。

今回はそのような問題に挑戦しましょう。

問題

次の計算をしなさい。
5^0（5の0乗）

※当メディアでは、「5の0乗」のような累乗を「5^0」と表します。

実は答えは「0」ではありません。正しい答えを求めることができるでしょうか。

解説

今回の問題の答えは「1」です。

「5を0回掛け算する」だから「0」だと考えた方が多いかもしれません。しかし、これは正しくありません。

5の0乗が1である理由は、結論からいうとそのように定義されているからです。
（累乗の計算ルールで、「0乗の計算結果は1」と決められている。ただし「0の0乗」だけは特別に扱うことがある）

では、なぜこのような定義がされているのでしょうか。

これは「計算規則の整合性を保つため」です。

5の3乗（5を3回掛け算）は125
5の2乗（5を2回掛け算）は25
5の1乗（5を1回掛け算）は5

「◯乗」の部分を1小さくするごとに、計算結果は「÷5」となります。

同様の規則で、さらに1小さくして「5の0乗」を考えると、1乗の計算結果をさらに「÷5」しなければいけません。

つまり5÷5=1となります。

また「0乗の計算結果を1」と定義することで、次の指数法則も成り立ちます。

(a^n)×(a^m) =a^(n+m)

もし「0乗の計算結果を0」とすれば、これは成り立たなくなります。

「0乗の計算結果が1」というのは直感とは反しますが、計算法則を保つためには自然な定義だと言えますね。

まとめ

今回の記事では「0乗の計算結果が1」となる理由を解説しました。

「なぜ」ということを考えることによって、より深く理解ができるようになるはずです。

ぜひ他の記事の問題にも挑戦してみてください！

※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。
あくまでも一例のご紹介に留まることを、ご了承ください。

---

---

文（編集）：SAJIMA
日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」

---

スピード勝負！他の問題にも挑戦しよう！