コンビニで買える『コーヒー牛乳』凄すぎ！８３キロ嫁がまるで別人
PR(株式会社ファンファレ)
大人になると、「立体の体積を求める」という場面はほとんどなくなります。
そのため、学生の頃に覚えた公式を思い出せないという人も多いかもしれません。
今回は「円錐（えんすい）」の体積を求める問題に挑戦してみましょう。
問題
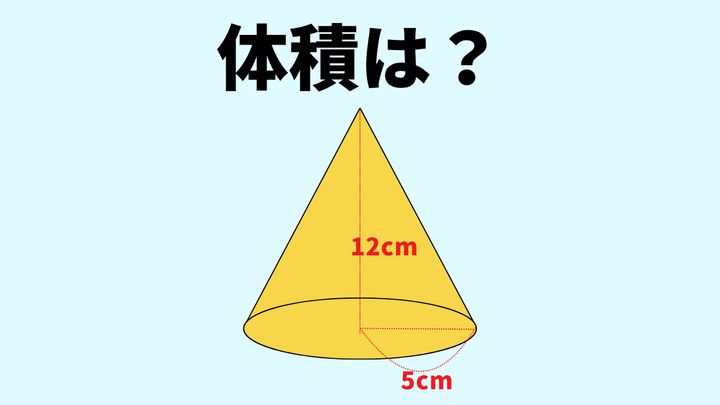
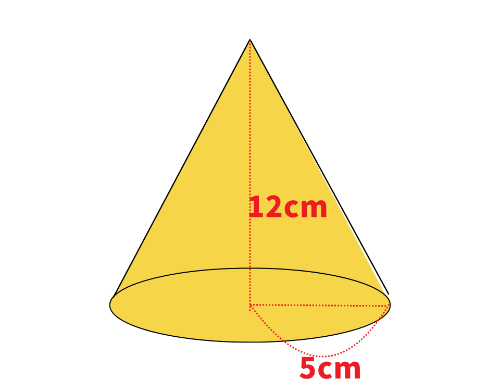
次の円錐の体積を求めなさい。
（底面が半径5cmの円で、高さが12cmの円錐。円周率は3.14とする）
正しく計算して答えを導けるでしょうか。
解説
今回の問題の答えは「314(cm3)」です。
どのように求めるのか、順を追って確認していきましょう。
まず、円錐の体積は次の公式で求めます。
円錐の体積=底面積×高さ×(1/3)
底面が半径5cmの円なので、底面積は次のように計算できます。
底面積
=5×5×3.14
=25×3.14
=78.5(cm2)
次に体積を求めます。
円錐の体積
=78.5×12×(1/3)
=78.5×4
=314(cm3)
したがって、答えは「314(cm3)」となります。
円錐の体積について
円錐は、底面が円形で頂点が一点に集まった形をしています。
このような形の立体は「錐体（すいたい）」と呼ばれ、底面の形に応じて「三角錐」「四角錐」「円錐」と名前が変わります。
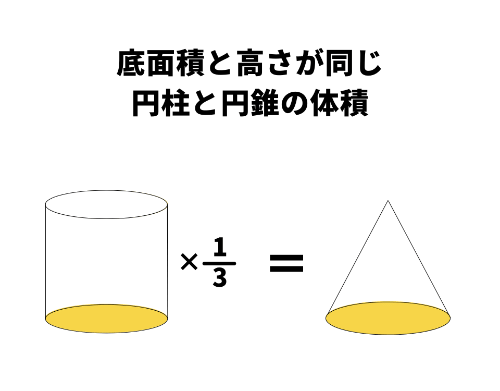
錐体の体積は、同じ底面積・同じ高さをもつ円柱や角柱の3分の1になるという性質があります。
まとめ
円錐の体積は、「底面積×高さ×1/3」で求めることができます。
底面が円の場合は、まず「半径×半径×円周率」で底面積を出すのがポイントです。
公式をしっかり覚えておくと、どんな立体の体積でもスムーズに求められるようになります。
※当メディアでご紹介する数学関連記事においては、複数の解法を持つものもございます。
あくまでも一例のご紹介に留まることを、ご了承ください。
文（編集）：SAJIMA
日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」
スピード勝負！他の問題にも挑戦しよう！
