対称群はその名の通りものの対称性を表した群で, 正四面体や正二十面体など多面体の対称性で表現することが一般的ですが, 本稿ではCayleyグラフという道具をもって対称群を再考します.

Cayleyグラフ

　Cayleyグラフの定義はいくらか散見されますが

• ノードを群の元と対応させる

• エッジを生成系の元と対応させる

ということはおおよそ共通しているようです. Cayleyグラフには, 多面体の表現よりも群としての構造が視覚的に分かりやすいという利点があります.

　ただ, ここでは諸々の都合により, この定義に以下のような若干のアレンジを加えておきます.

• ノードを対称群が作用するn点集合の状態と対応させる

• エッジを生成系の元と対応させる

• エッジの彩色で生成元を区別する

• エッジは互換なら無向, 長さ3以上なら有向

　最初の規則だけ分かりづらいと思われるため, 補足します. 例えば, 3次対称群S_3は順序対の集合

\Omega_3=\lbrace\langle1,2,3\rangle,\langle1,3,2\rangle,\langle2,1,3\rangle,\\\langle2,3,1\rangle,\langle3,1,2\rangle,\langle3,2,1\rangle\rbrace

に作用して,

\begin{pmatrix}2&3\end{pmatrix}\langle3,1,2\rangle=\langle2,1,3\rangle

のように順序対の数字を交換します. 簡単のため, 本稿ではこれを略して

\begin{pmatrix}2&3\end{pmatrix}312=213

と書くことに決めます. ノードをn点集合の状態と対応させるというのは, この順序対にノードを対応させるということです.

下準備 - 生成系の構成法

　Cayleyグラフを考えるにあたって当然生成系が必要となるため, どのような生成元が対称群全体を生成するのか考えることから始めます. そのためにまずは2つの定理を持ち出します.

定理1 隣接互換

　S_nにおいて, \begin{pmatrix}1&2\end{pmatrix},\begin{pmatrix}2&3\end{pmatrix},\cdots,\begin{pmatrix}n-1&n\end{pmatrix}はS_n全体を生成する.

定理2 巡回置換と互換

　S_nにおいて, \begin{pmatrix}1&2&\cdots&n\end{pmatrix}と\begin{pmatrix}1&2\end{pmatrix}はS_n全体を生成する.

　これらの定理を一般化していくと, 以下に示すような生成系の構成法が浮かび上がります.

　n次対称群の長さnの巡回置換の生成系\langle\begin{pmatrix}a_1&a_2&\cdots&a_{n}\end{pmatrix}\rangleに対して次のような操作を考えます.

• 切り抜き：巡回置換の適当な部分をくり抜いて生成系に加える

• 切り取り：巡回置換を適当な箇所で切断することができる

　6次対称群を例に取って説明します. まずは適当な長さ6の巡回置換を取ってきます. これを\begin{pmatrix}1&3&6&2&4&5\end{pmatrix}としましょう. この置換が生成する部分群は\langle\begin{pmatrix}1&3&6&2&4&5\end{pmatrix}\rangleと書け, ここに操作を施していきます.
2の位置で切り取りを行うとと,

\langle\begin{pmatrix}1&3&6&2\end{pmatrix},\begin{pmatrix}2&4&5\end{pmatrix}\rangle

のように2つの巡回置換に分解されます. \begin{pmatrix}1&3&6&2\end{pmatrix}の136の部分に対して切り抜きを実行すれば

\langle\begin{pmatrix}1&3&6&2\end{pmatrix},\begin{pmatrix}2&4&5\end{pmatrix},\begin{pmatrix}1&3&6\end{pmatrix}\rangle

と, そのまま\begin{pmatrix}1&3&6\end{pmatrix}が加えられます. 実は, このような操作を順繰りに行っていったとき, 生成系の中に互換が現れればその生成系は対称群全体と等しくなるということが示せます. 厳密な証明は以下の記事をご覧ください.

　イメージとしては, 互換の自由度は非常に高く, 特定の巡回置換を分解して, すべての互換を生み出せるような性質を持っているため, 一つでも互換が紛れ込んでいれば対称群全体を生成できるといったところです. より厳密には, 紛れ込んだ互換と数字が重複している巡回置換により共役な互換が生成でき, そこから対称群全体を生成できるということです.

先ほどの6次の例に続けて切り取りを施すと,

\langle\begin{pmatrix}1&3&6&2\end{pmatrix},\begin{pmatrix}2&4&5\end{pmatrix},\begin{pmatrix}1&3\end{pmatrix},\begin{pmatrix}3&6\end{pmatrix}\rangle

と, 互換が挿入され, これは6次対称群全体と等しいと言えます.

　ただ, この方法はあくまで対称群全体を生成する系を生み出すものであって, 冗長な生成系を取り除けません. 冗長とは, 生成系のある生成元が他の生成元の積によって表せてしまうことで, 例えば3次対称群では, すべての互換からなる生成系\langle\begin{pmatrix}1&2\end{pmatrix},\begin{pmatrix}2&3\end{pmatrix},\begin{pmatrix}1&3\end{pmatrix}\rangleはS_3と等しいことはすぐに分かります. しかし, この生成系は

\begin{align*} \begin{pmatrix}1&3\end{pmatrix}=\begin{pmatrix}1&2\end{pmatrix}\begin{pmatrix}2&3\end{pmatrix}\begin{pmatrix}1&2\end{pmatrix}\\ =\begin{pmatrix}2&3\end{pmatrix}\begin{pmatrix}1&2\end{pmatrix}\begin{pmatrix}2&3\end{pmatrix} \end{align*}

と, 生成元である\begin{pmatrix}1&3\end{pmatrix}が他の生成元の積によって書けてしまうという意味で冗長なのです. Cayleyグラフの簡素さや一意性の観点から, このような冗長な生成系は認めないこととします.

　以上の方法を使って, これからS_3,S_4を見ていくわけですが, 念のため, この方法で対称群の冗長でない生成系をすべて構成できるとは主張していないことを断っておきます.

3次対称群 - 六角形, 三角柱

　3次対称群に対して操作を行うと以下のような列が出来上がります. \begin{pmatrix}1&2&3\end{pmatrix}から始めていますが, \begin{pmatrix}1&3&2\end{pmatrix}から始めても議論は同様に進み, Cayleyグラフは同型になります.

　まずは\langle\begin{pmatrix}1&2\end{pmatrix},\begin{pmatrix}2&3\end{pmatrix}\rangleのCayleyグラフを観察することにします.

　見ての通り, グラフは六角形になっており, 対角線の移動は\begin{pmatrix}1&3\end{pmatrix}に, それ以外の移動は長さ3の巡回置換\begin{pmatrix}1&2&3\end{pmatrix},\begin{pmatrix}1&3&2\end{pmatrix}に対応しています. \begin{pmatrix}1&2\end{pmatrix}と\begin{pmatrix}2&3\end{pmatrix}だけでは限られた操作しか許されず, 考えられるのは, どちらの互換を先に計算するか, 2つの互換を何回重ねるかというパラメータのみで, かつ自由群のように無限に2つの互換を重ねることはできず, どちらから始めても必ず6回で元に戻ってしまうため, 1次元の線分の端と端が繋がり, 六角形になっていると解釈できます.

　次に, \langle\begin{pmatrix}1&2&3\end{pmatrix},\begin{pmatrix}1&2\end{pmatrix}\rangleは

のようになっていて, 三角柱と同型であることが見て取れます. すぐに分かることですが, 正n角形の回転移動と鏡映反転の群である二面体群D_nのCayleyグラフはn角柱となっていて

S_3\cong D_3

ということが視覚的に理解できます. 赤の\begin{pmatrix}1&2\end{pmatrix}は鏡映反転, 緑の\begin{pmatrix}1&2&3\end{pmatrix}は回転移動に対応しています. 頂点が1,2,3である三角形の回転移動と鏡映反転を考えれば, このことも納得できるでしょう.

4次対称群 - 切頂八面体, 切頂六面体

　4次対称群については, 以下のような操作の列が得られます.

　まずは\langle\begin{pmatrix}1&2\end{pmatrix},\begin{pmatrix}2&3\end{pmatrix},\begin{pmatrix}3&4\end{pmatrix}\rangleで, 4次の隣接互換からなる生成系です.

　3次と比較すると大分複雑になっていますが, 上のグラフは切頂八面体と同型になっています. 切頂八面体とは, 正八面体の各頂点を切り落とした多面体で, 赤-黄の四角形が6つ確認できますが, これが八面体の頂点の切り口だと見れば, 切頂八面体と同型なグラフだと理解できるでしょう. 

\begin{align*} S_3&\cong\langle\begin{pmatrix}1&2\end{pmatrix},\begin{pmatrix}2&3\end{pmatrix}\rangle\\ &\cong\langle\begin{pmatrix}2&3\end{pmatrix},\begin{pmatrix}3&4\end{pmatrix}\rangle \end{align*}

のようにS_3と同型な部分群が含まれているため, 節々に六角形が確認できます. 赤-橙の六角形は4を, 橙-黄は1を動かさないという部分群になっており, それぞれ4つ取り出すことができます.

　次は, \langle\begin{pmatrix}1&2\end{pmatrix},\begin{pmatrix}2&3&4\end{pmatrix}\rangleです.

　このグラフは切頂六面体と同型になっています. 切頂六面体も切頂八面体と同様に, 六面体, つまり立方体の角を切り落とした多面体で, 緑の三角形が元の立方体から削り取られた部分だと見れば, 切頂六面体に見えてくるかと思います. また, S_4を正四面体の各頂点の交換だと解釈すれば, 緑の三角形は1点を固定して, 底面の三角形を回すという操作に対応していると考えられます. 一方, \begin{pmatrix}1&2\end{pmatrix}の方は固定していた点と底面の三角形の頂点を交換することを表していて, \langle\begin{pmatrix}1&2\end{pmatrix},\begin{pmatrix}2&3&4\end{pmatrix}\rangle=S_4は上記の2つの操作のみで正四面体のあらゆる状態を再現できるとも読むことができます.

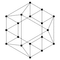
　最後に, \langle\begin{pmatrix}1&2\end{pmatrix},\begin{pmatrix}1&2&3&4\end{pmatrix}\rangleです.

　先ほどと同じ切頂八面体ではありますが, 有向辺が紛れ込んでいます. こちらも\langle\begin{pmatrix}1&2\end{pmatrix},\begin{pmatrix}2&3&4\end{pmatrix}\rangleの時と同様に, 正四面体の回転と2点交換からなる操作の群だと解釈できますが, \begin{pmatrix}1&2&3&4\end{pmatrix}は正四面体を捻って回転させるという点で違いがみられます.