小学校で習った分数の計算ルール、今でも正確に覚えているでしょうか?
今回は、帯分数の混じった計算にチャレンジしてみましょう。また、同じ式の中には負の数の引き算も登場します。
分数と負の数、二つの計算知識を復習するチャンスですよ。
問題
次の計算をし、帯分数の形で答えなさい。
(2+2/5)÷(2+1/10)+3−(−1)
解答
正解は、「5+1/7」です。
どうやって計算をすればよいか、分かりましたか?
次の「ポイント」では、この問題の計算過程を確認できます。
「答えが間違っていた」「途中で躓いてしまい計算が進まなかった」という人は、ぜひご覧ください。
ポイント
この問題のポイントは、「帯分数の整数部分の扱い方」にあります。
帯分数とは、整数と真分数(分子が分母より小さい分数)を組みわせた分数のことです。帯分数を使うと、1よりも大きな数を分数で表せます。今回の問題でいえば、(2+2/5)や(2+1/10)が帯分数になります。
なお、本来帯分数では+記号を書かないのですが、本記事では整数部分と分子部分の区別をつけやすいように+記号を用いて帯分数を表しています。
1よりも大きな数を表すことができる分数には、帯分数の他に仮分数※があります。仮分数は、数をすべて分数で表します。そのため、1より大きな数を仮分数で表すとき、分子は分母よりも大きくなります。例えば、10/7は仮分数です。
※仮分数は、分子が分母よりも大きいか等しい分数のことなので、1を表すこともできます。
ここで、改めて今回の問題を見てみましょう。
(2+2/5)÷(2+1/10)+3−(−1)
最初に、帯分数の割り算「(2+2/5)÷(2+1/10)」をします。
帯分数の計算の仕方には、二種類あります。一つは「帯分数を仮分数に直して計算する」方法、もう一つは「帯分数のまま計算する」方法です。ただし、後者の方法が使える場面は限定的です。
帯分数の割り算は、「帯分数を仮分数に直して計算する」方法で計算します。
帯分数を仮分数にするには、整数部分を隣の真分数の分母を持つ分数に変えて、真分数と足し合わせます。早速やってみましょう。
2+2/5の2は10/5のことだから
2+2/5=10/5+2/5=12/5
2+1/10の2は20/10のことだから
2+1/10=20/10+1/10=21/10
これで、割り算部分は次のように変形できます。
(2+2/5)÷(2+1/10)
=12/5÷21/10←仮分数の割り算
では、さっそく計算していきましょう。
分数の割り算では、割る数の分子分母を逆にした分数(逆数)を掛けます。
12/5÷21/10
=12/5×10/21
また、分数の掛け算では、分子どうし、分母どうしをそれぞれ掛け合わせます。掛け算の途中に約分(同じ数で分子分母を割ること)ができるときは、約分してください。計算が楽になりますよ。
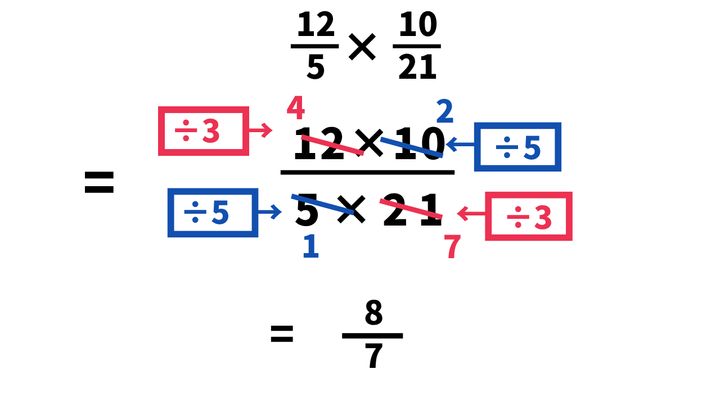
12/5×10/21
=(12×10)/(5×21)
=(4×2)/(1×7)←約分の仕方は下図を参照してください
=8/7
今回の問題は、帯分数で答えを出すことになっているので、8/7は1+1/7と帯分数に直しておきます。
これで式は以下の形になりました。
(2+2/5)÷(2+1/10)+3−(−1)
=(1+1/7)+3−(−1)
続きの計算をしていきましょう。
帯分数と整数の足し算は、「帯分数のまま計算する」方法が使えます。これは、帯分数の整数部分に数を足すだけなので簡単です。
(1+1/7)+3−(−1)
=(1+3)+1/7−(−1)←帯分数の整数部分1に3を足す
=(4+1/7)−(−1)
最後は負の数の引き算ですが、実はこれ、正の数の足し算にできます。
<負の数の引き算>
−(−■)=+■
つまり、先ほどと同じく、帯分数の整数部分に数を足すだけでよいのですね。
(4+1/7)−(−1)
=(4+1/7)+1←正の数の足し算にする
=(4+1)+1/7←帯分数の整数部分4に足す
=5+1/7
これで答えが出ました。
まとめ
帯分数の計算は、仮分数に直してする方法と、帯分数のままする方法があります。
帯分数の割り算は仮分数に直さないと計算できません。一方で、帯分数と整数の足し算をする場合は、帯分数のままでも計算ができます。
実は、帯分数も整数も仮分数に直して足し算することもできるのですが、手間がかかります。帯分数のまま楽に計算ができるなら、無理に仮分数に直す必要はありません。
帯分数の計算方法を思い出してきたという人は、ぜひ、帯分数の引き算や掛け算の方法についても調べてみてください。
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。
文(編集):VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。
スピード勝負!他の問題にも挑戦しよう!