工夫して10秒で計算してみて！「8/9119÷2/9119」→暗算できる？

分数の計算はややこしくて苦手という人にぜひ挑戦してほしいのが、今回の問題です。

分母がとても大きい分数の割り算ですが、実は10秒以内に計算できる方法が存在します。

どうやって計算したらよいのか、考えてみてください。

問題

次の計算を暗算でしなさい。
8/9119÷2/9119

※制限時間は10秒です。

解答

正解は、「4」です。

分母の9119を見て「難しい！」と計算をあきらめてしまった人もいるかもしれませんね。

この問題を10秒以内に計算する工夫とは、どんなものなのでしょうか。

次の「ポイント」で確認してみましょう。

ポイント

この問題のポイントは、「割られる数、割る数の分母が同じであること」です。

8/9119÷2/9119

割り算では、割られる数と割る数に同じ数を掛けて計算しても元の式と答えが同じになります。この仕組みを使って、今回の問題を簡単にしてみましょう。

問題に出てくる8/9119と2/9119の分母はどちらも9119です。ということは、割られる数と割る数ともに9119を掛ければ、この割り算は整数の割り算に変形できますね。

では、実際にやってみましょう。

8/9119÷2/9119
=(8/9119×9119)÷(2/9119×9119)←割られる数と割る数に同じ9119を掛ける
=8÷2
=4

一見複雑に見えた今回の問題ですが、実は8÷2というとても簡単な割り算と同じ意味を持つ式だったのです。

なお、分数の割り算ルールを使ってこの問題を計算すると、次のようになります。

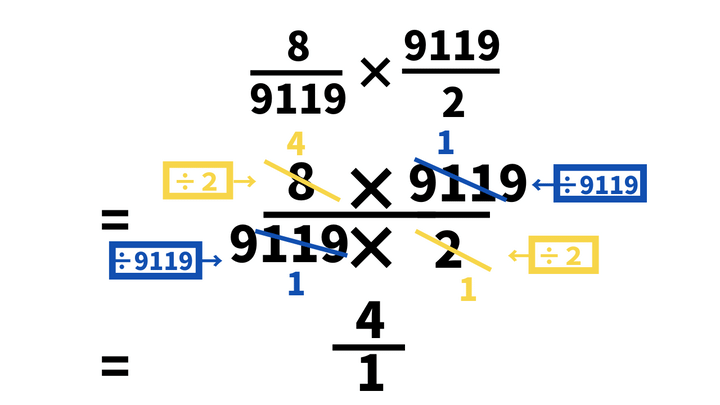
8/9119÷2/9119
=8/9119×9119/2←分数の割り算では割る数を逆数にして掛ける
=(8×9119)/(9119×2)←分数の掛け算では分子どうし、分母どうしを掛ける
=(8×1)/(1×2)←分子と分母の9119を約分
=(4×1)/(1×1)←分子と分母を÷2して約分
=4/1
=4

約分とは、分子と分母を同じ数で割って簡単な数で分数を表すことです。

分数では、分子と分母を同じ数で割っても大きさは変わりません。ここで紹介した計算過程では、掛け算をする前に約分しています。こうすると式が簡単になり、4という計算結果が楽に出せます。

この分数の割り算の計算過程と、先に紹介した「割られる数と割る数に9119を掛ける」計算過程を見比べると、結局は同じ計算をしていることに気が付きませんか？

どちらも邪魔な9119という数を先に消して、計算を簡単にしているところに注目してください。

まとめ

今回は、共通の大きな分母を持つ分数どうしの割り算にチャレンジしました。

分母が大きい数だと計算がとても難しく見えるかもしれませんが、割られる数・割る数の分母が共通であれば、その分母を掛けて式を簡単にしてしまえばよいのです。割り算では、割られる数と割る数に同じ数を掛けて計算しても、元の式と答えが同じになるからです。

ちなみにこの割り算の特徴をうまく使っているのが、小数の割り算の計算ルールです。この問題にチャレンジしたついでに、小数の割り算の復習もしてみてはどうでしょうか？

※当メディアでご紹介する数学関連記事において、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

---

---

文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。

---

スピード勝負！他の問題にも挑戦しよう！