これどうやって計算するか覚えてる？「この平行四辺形の面積は？」→正しく答えられる？

図形の問題の基本となるのが、「面積の公式」です。

小学校のときには、図形の種類ごとに面積の公式を習いましたね。さて、大人になってからもこの公式の内容を覚えているでしょうか？

今回は、平行四辺形の面積を求めてみましょう。

問題

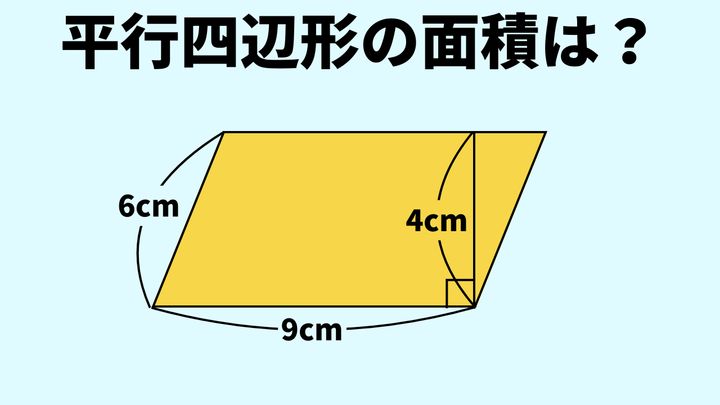
次の平行四辺形の面積を求めてください。

正解は、「36cm2」です。

54cm2と答えてしまった人はいませんか？

平行四辺形の面積を求める計算の「ポイント」を、次項で確認してみましょう。

この問題のポイントは、「平行四辺形の高さ」です。

まずは、「平行四辺形の面積の公式」を確認してください。

<平行四辺形の面積>
底辺×高さ

ここで、もう一度今回の問題を見てみましょう。

画像には三つの長さが書かれています。底辺を9cmの辺と見たとき、高さは6cmだと思うかもしれませんが、これは間違いです。

9×6=54cm2 ←誤答!

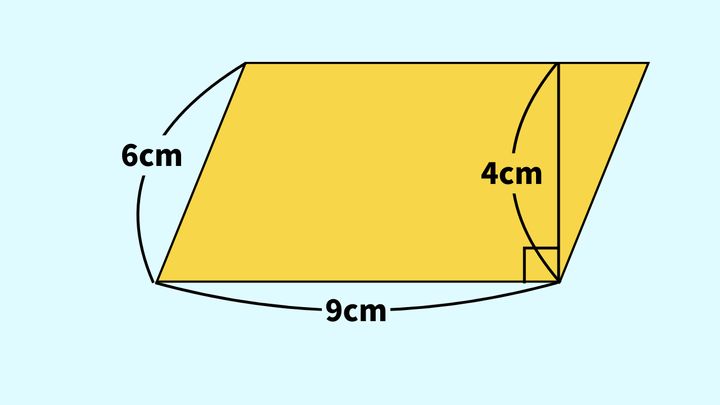
実は、この平行四辺形の高さは「4cm」になります。平行四辺形の高さとは「底辺と平行な辺との間の距離」だからです。この距離は、二つの辺と90度で交わっている線の長さで表されます。

平行四辺形の向かい合う辺は平行ですから、底辺と見た9cm（下の横の辺）と上の横の辺二つは平行です。よって、横二つの辺と90度で交わっている線の長さ=この平行四辺形の高さといえます。

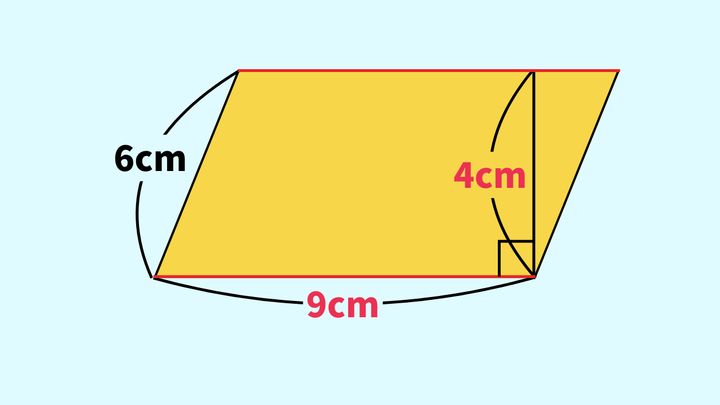
図を見ると、底辺と90度で交わっているのは、6cmの辺ではなく、4cmの直線ですね（図の□は90°を表す記号です）。よって、底辺を9cmとしたとき、この平行四辺形の高さは4cmです。

つまり、この平行四辺形の面積を求める式は、次のようになります。

9×4=36cm2

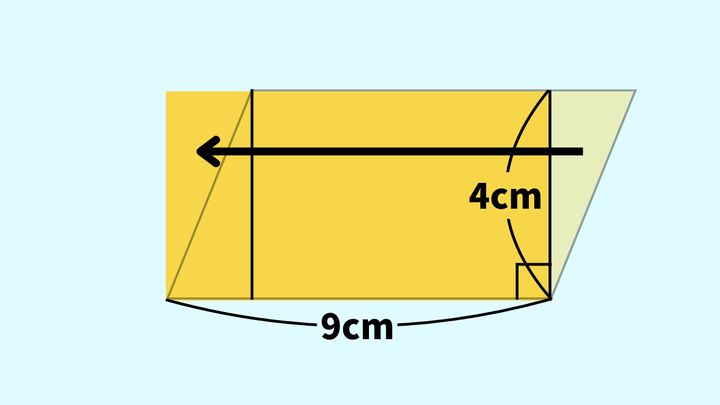
平行四辺形の面積の公式が、底辺×高さである理由は、平行四辺形を長方形に変形すれば分かります。

上の図のように、高さの線で切ってできる三角形を移動して反対側にくっつければ、長方形ができます。この長方形の面積は、次の式で求められます。

長方形の面積：縦×横
4cm×9cm=36cm2

この「4cm×9cm=36cm2」は、平行四辺形の面積の公式「底辺×高さ」を使って作った式と一致しますね。こうしてみれば、6cmの辺の出番はないことが一目瞭然です。

今回は、平行四辺形の面積を求める問題にチャレンジしました。

平行四辺形の面積は、「底辺×高さ」で求められます。高さは底辺と垂直に交わっている線の長さです。平行四辺形の辺の長さが高さに見えることも、混同しないようにしましょう。

公式が成り立つのは、平行四辺形を長方形に変形できるからです。公式の背景を理解できていれば、長方形の面積の公式を使って平行四辺形の面積を算出することもできますよ。

※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。

類似の数学問題にもう1問挑戦！

一辺の長さがわかればスルスル解ける！「面積クイズ」→□に当てはまる数は？