図形の問題に苦手意識を持っている人は多いのではないでしょうか。特に応用的な図形の問題は、一定のルールに沿って計算すれば必ず正解できるわけではない難しさがあります。
しかし、図形の問題にはちょっとした視点の転換で解法が見えてくる「パズル的な面白さ」もありますよ。
今回はそんな問題に挑戦してみましょう!
問題
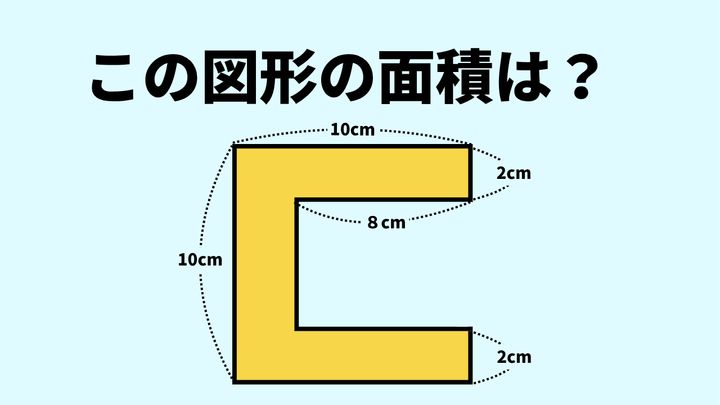
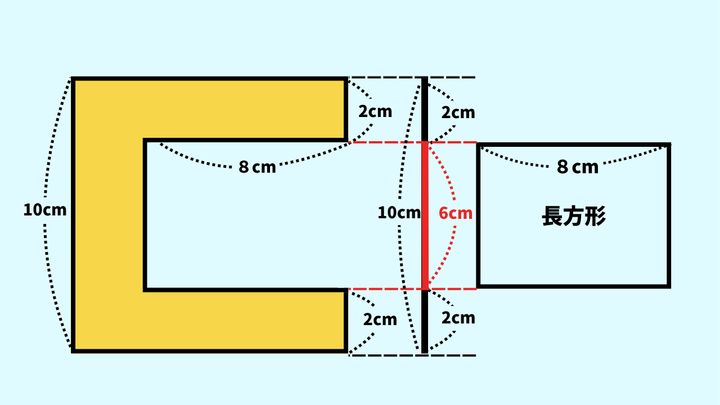
次の図形(黄色で塗りつぶされた部分)の面積を求めなさい。
※角はすべて直角。
※上下の長辺の長さは等しい。
※長さや面積の縮尺は、必ずしも正確に描かれていない。
解答
正解は、「52cm2」です(※当メディアでは「平方cm」を「cm2」と表記します)。
どうやって答えを出せばよいか、分かりましたか?
スムーズに計算するには、黄色い図形をどのような形としてとらえたかが重要です。
次の「ポイント」で、この問題の考え方を詳しく見ていきましょう。
ポイント
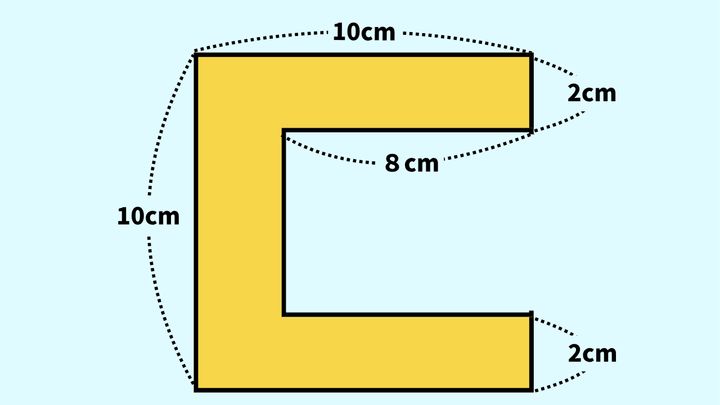
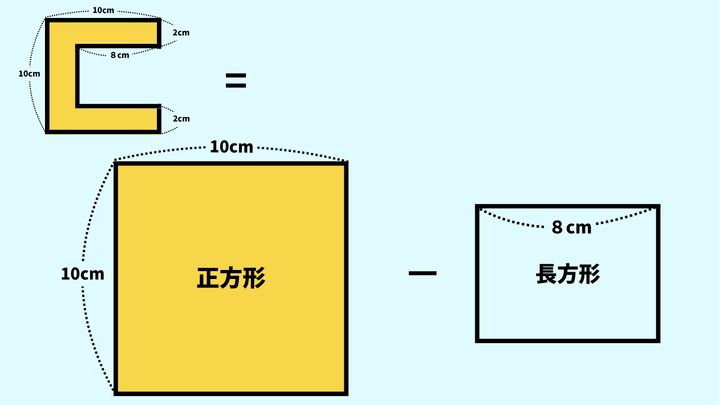
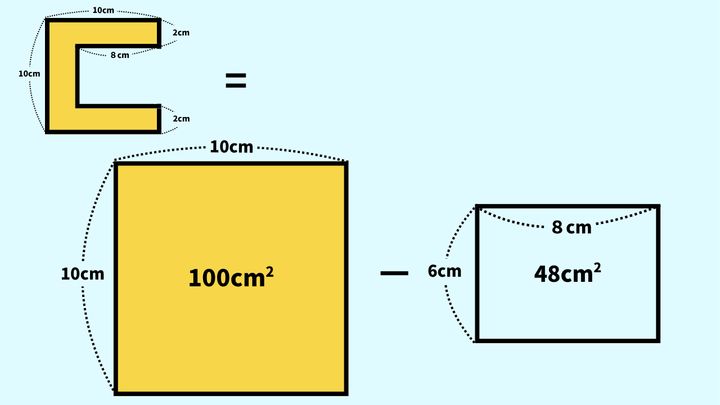
この問題のポイントは、黄色い図形を「正方形から長方形を引いた形」としてとらえることです。
つまり、以下の図のように図形を見てみましょう。
このような図形の見方をすると、次の三つのステップで「黄色い図形の面積」が出せると分かるでしょう。
1.正方形(上の図の黄色い長方形)の面積を求める
2.長方形(上の図の水色の長方形)の面積を求める
3.正方形の面積から長方形の面積を引く
では、順番にやっていきましょう。
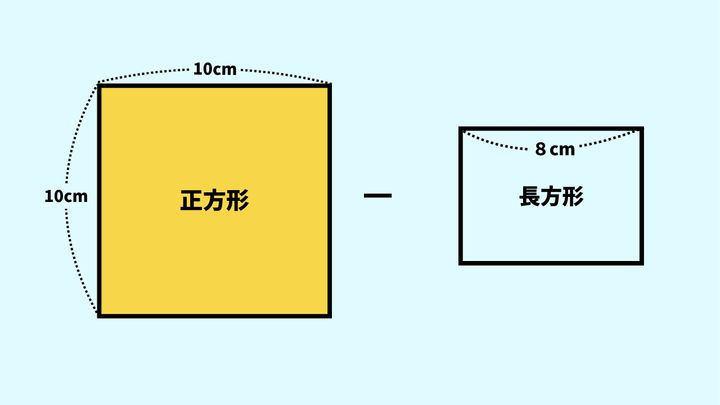
1.正方形の面積を求める
以下の図の通り、正方形の一辺の長さは10cmと分かっています。
正方形の面積の公式=一辺×一辺
公式に当てはめて面積の計算をすると、次のようになります。
10cm×10cm=100cm2
2.長方形の面積を求める
次に、長方形の面積を求めましょう。
長方形の面積の公式=縦の長さ×横の長さ
公式を使うためには、水色の長方形の縦と横の長さが必要です。
しかし、長方形の横の長さは分かっていますが、縦の長さが分かりません。
そこで元の図形に戻って、長方形の縦の長さを考えてみましょう。
長方形の縦の長さは、元の黄色い図形の縦の長さ10cmから上下2cmずつ引いた長さと一致します(上図の赤い実線部分)。
10cm−2cm−2cm
=6cm
縦は6cm、横は8cmだと分かったので、長方形の面積の公式が使えます。
6cm×8cm
=48cm2
3.正方形の面積から長方形の面積を引く
最後に、正方形の面積から長方形の面積を引いて答えを出します。
正方形の面積は100cm2、長方形の面積は48cm2なので、元の黄色い図形の面積を求める式は以下のようになります。
100cm2−48cm2
=52cm2
これで答えが出ましたね。
まとめ
今回のように正方形や長方形の中に一部の空白がみられる「欠けた図形」の問題はよく出題されます。
このような問題では、まず空白部分を無視して「欠けていない図形」の面積を求めます。次に「欠けている部分」の面積を求めます。最後に「欠けていない図形」から「欠けている部分」を引いて、元の図形の面積を算出します。
この方法を覚えておくと、さまざまな図形の問題に応用が利きますよ。
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。
文(編集):VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。
もう一問挑戦!