今回は、図形の角度を求める問題に挑戦してみましょう。
「角度を求める」と言っても、分度器を使う必要はありません。
図形の性質を理解していれば、計算だけで角度を導き出すことができます。
問題
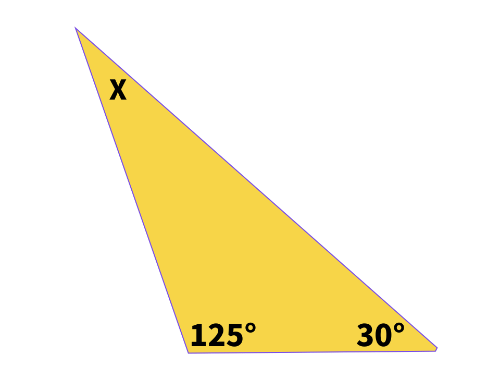
次のxの角度を求めなさい。
三角形の三つの角のうち、二つの角度(125°と30°)が分かっています。
残り一つの角xをどのようにして求めればよいでしょうか。
解説
今回の問題の答えは「25°」です。
順を追って考えてみましょう。
三角形の角度を求めるときに必ず使う性質は、次の通りです。
三角形の内角の和は180°である。
どのような三角形でも、三つの角を足すと180°になります。
したがって、残りの角度は次のように計算できます。
180−(125+30)
=180−155
=25
よって、求める角度は「25°」となります。
三角形の内角の和は180°である理由
角度の計算では「三角形の内角の和は180°」という性質を使いました。
この性質がどのような三角形でも成り立つ理由を簡単に確認しておきましょう。
角A=a
角B=b
角C=c
となる三角形を考えます。
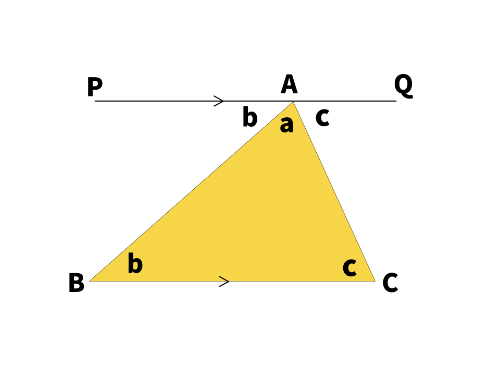
この三角形の辺BCに平行で、点Aを通る直線PQを引きます。
平行線の錯角の性質から、
角PAB=b
角QAC=c
となります。
P、A、Qは一直線上にあるため、
a+b+c=180°
つまり、三角形の内角の和は180°であることがわかります。
※錯角:
一つの直線が二つの直線と交わるとき、二直線の内側にできる四つの角のうち、斜め(対角)に位置する角。上図では「角PABと角ABC」「角QACと角ACB」の関係。二直線が平行のとき、これらは等しくなります。
まとめ
三角形の内角の和は必ず180°になるという性質は、角度を求めるときに非常に重要です。
複雑に見える図形の問題でも、足し算・引き算で簡単に解くことができます。
この基本をしっかり押さえておきましょう。
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。
あくまでも一例のご紹介に留まることを、ご了承ください。
文(編集):SAJIMA
日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」
意外と忘れがち!面積問題まとめ!