今回は複雑な図形の面積を求めてみましょう。
長方形や円などと違って、一発で答えを求める公式がない形なので、頭を柔らかくして考えてみることが重要です。
また、辺の長さも全てがわかっているわけではないので、限られた情報をどう使うか、情報を的確に扱う力も試されますよ。
問題
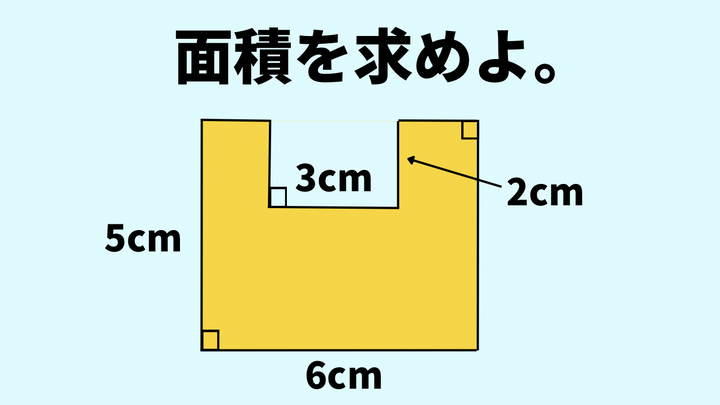
次の図形の面積を求めなさい。
どちらかというと長方形に近い形ですね。
解説
この問題の答えは「24cm2」です。問題の図形は上の一部だけがへこんでいる凹形ですね。この形の図形の面積を求める方法はいくつかありますが、今回は辺の長さが全て分かっているわけではないので、解き方が限定されてしまいます。
どうやって解けるかというと、面積問題においてよく使われる〈大きい面積−小さい面積〉の計算を行います。
〈大きい面積−小さい面積〉
・図形の一部が欠けているような場合に使用できる。
・図形が欠けていないものとして、それを大きい面積とする。
・欠けた部分を小さい面積とする。
・大きい面積−小さい面積を計算すると、残りの知りたい面積となる。
では手順通りに大きい面積と小さい面積を求めていきましょう。
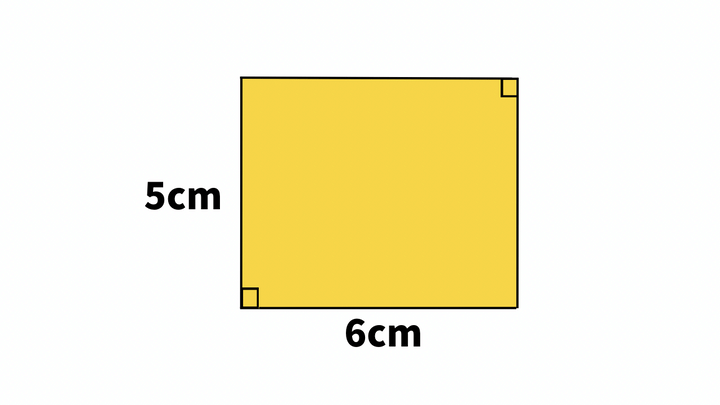
大きい面積は縦が5cm、横が6cmの長方形です。
面積を求めます。
大きい面積
=5×6
=30
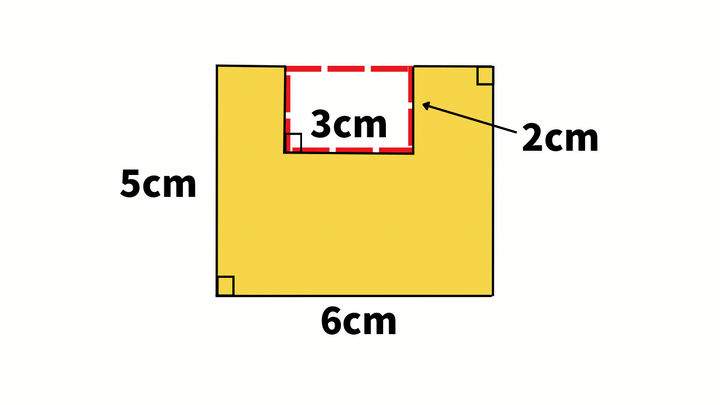
次に小さい方の面積を求めます。
こちらは縦が2cm、横が3cmの長方形ですね。
小さい面積
=2×3
=6
よって、もともとの凹形の面積は
凹形
=30−6
=24
答えは「24cm2」となります。
まとめ
全体の長方形から赤い点線部分を引くことによって黄色い凹部分だけを残すことができました。
公式一発で求めることができない複雑な形の面積はこのように工夫をして求めていきましょう。
※当メディアでご紹介する数学関連記事において、複数の解法を持つものもございます。 あくまでも一例のご紹介に留まることを、ご了承ください。
文(編集):うおうお
数学の教員免許を所持。個別指導・集団指導の学習塾で数学の講師として小学生から高校生までの指導や、小学生の宿題指導を通して算数の魅力を深堀して楽しく伝えている。現在は民間学童保育所で放課後児童支援員として勤務しながらフリーランスで受験指導もしている。
もう一問挑戦!