これどうやって計算するか覚えてる？「この三角形の角度は？」→正しく計算できる？

三角形の角度を求める問題は、図形の分野でよく出題されます。

今回は、二つの三角形の角度を組み合わせて答えを求める問題にチャレンジしてみましょう。

少し応用的な内容になりますが、よく出題される形なので、ぜひ答えの出し方を確認してください。

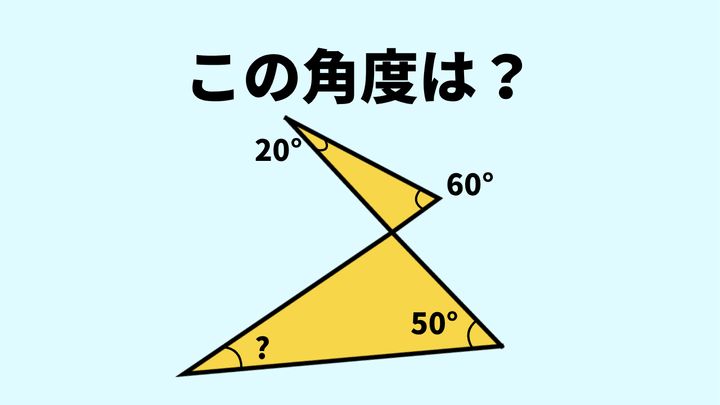
問題

?に当てはまる三角形の角度を求めなさい。

正解は、「30°」です。

まず、基本事項として「三角形の三つの角の合計は必ず180°になる」ことを押さえておきましょう。ここから考えを広げていけば、この問題の計算方法が分かるはずです。

次の「ポイント」では、30°という正解にたどり着くまでの考え方を解説していきます。ぜひ、ご覧ください。

この問題のポイントは、「共通の外角に注目すること」です。

外角とは、多角形の一辺の延長線と隣の辺との間にできる角のことです。図形の外側にできる角だと覚えておくと、分かりやすいですよ。

さて、下の図を見てください。この図の外角はAとCの角度を合計したものになります。

なぜなら、「三角形の三つの角の合計は必ず180°になる」のでA+B+C=180°、さらに外角とBの角を足すと一直線が生まれるので外角+B=180°だからです。

A+B+C=180°⇔(A+C)+B=180°
外角+B=180°

A+C＝外角

AやCと隣り合う外角でも同じことが言えます。よって、三角形の外角は、「外角と隣り合わない二つの内角の合計と大きさが同じ」だといえます。この性質が今回の問題を解くカギになります。

さて、この問題には上と下、二つの三角形があります。

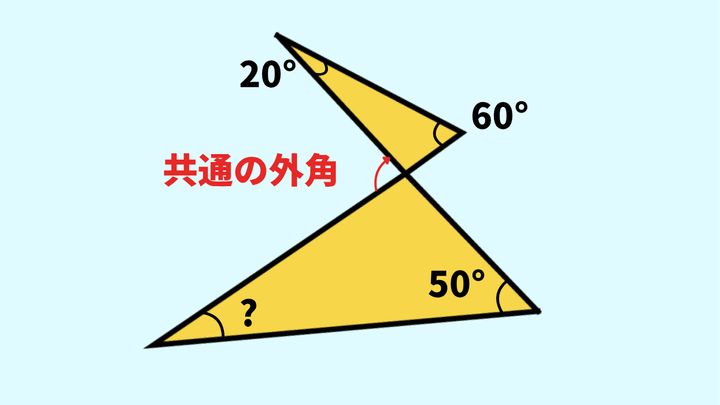
下図を見てください。二つの三角形で共通の外角が中央にあるのが分かりますね。

まずは上の三角形に注目し、この外角の大きさを求めてみましょう。外角は「隣り合わない二つの内角の合計と大きさが同じ」なので、20°+60°=80°が成り立ちます。

次に下の三角形に注目します。80°は下の三角形の外角の大きさでもありますから、?+50°=80°になるはずです。

これで?に当てはまる数は、30°だと分かりますね。

20°+60°=80°←共通の外角の大きさを求める
?+50°=80°より?=30°

次のように計算してもOKですよ。

20°+60°=?+50°←共通の外角に注目すると20°+60°と?+50°は等しいことが分かる
80°=?+50°
?=30°

二つの三角形が共通の外角でつながった形は、応用的な角度の問題として頻出です。

このような問題では、まず共通の外角に注目してください。三角形の外角の大きさは「隣り合わない二つの内角の合計」で求められます。外角の大きさを手掛かりにすれば、不明になっている角度の大きさが見えてきます。

図形の応用問題は一見難しそうですが、解き方がある程度確立されている典型的なものも多いです。最初に見たときは考え方が分からなくても、解説をしっかり読むことで次につながりますよ。

※当メディアでご紹介する数学関連記事において、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。

もう一問挑戦！

大人が意外と解けない数学「xの角度は？」→どうやって求める？