これどうやって計算するか覚えてる？「角度が不明な三角形」→この角度は？

三角形の角度を求める問題は、図形問題の中の基本と言えるでしょう。

角度が分かると、不明だった図形の辺の長さや面積が次々と求められるようになることもありますよ。

今回の問題を通して、三角形の角度の性質を復習してみましょう。

問題

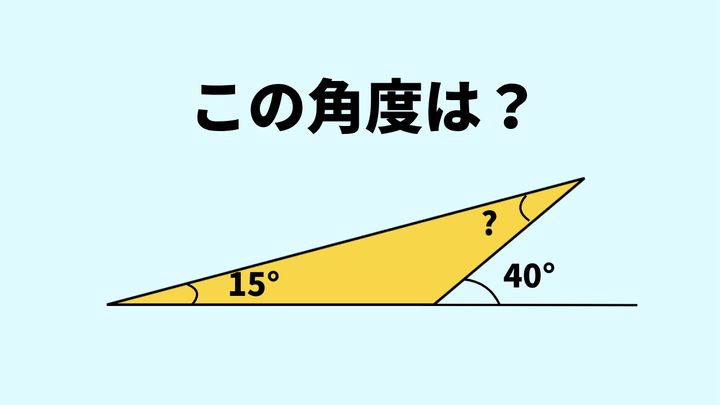
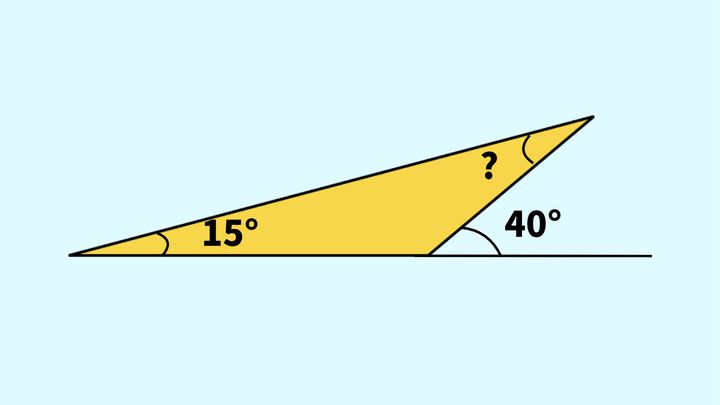
？に当てはまる角度を求めなさい。

正解は、「25°」です。

どうすればこの角度が計算できるのか、分かりましたか？

次の「ポイント」で、問題の考え方を確認してみましょう。

この問題のポイントは、「外角を上手に使うこと」です。

まず「三角形の内角（内側にできる角）の合計は180°になる」という性質を思い出してください。

この性質を使うと、三角形の内角のうち二つの角度が分かっていればもう一つの角度を求めることができます。

例：20°と30°の内角を持つ三角形のもう一つの角度?を求める場合
20°+30°+?=180°
?=180°−20°−30°=130°

しかし今回、三角形の内角で分かっているのは15°のみに見えます。

40°は三角形の外側にできる角度（外角といいます）なので、15°+40°+?=180°のような関係は成り立ちません。

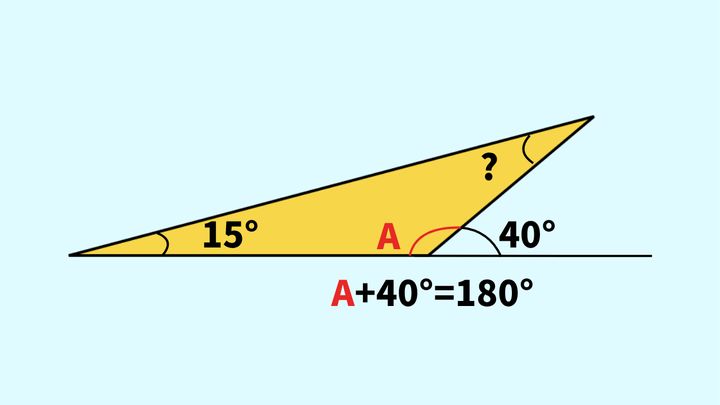
しかし、心配する必要はありません。40°と隣り合う三角形の内角Aを足すと、一直線、つまり180°になります。よって、次のように内角Aの角度を求められます。

40°の外角の隣の内角をAとすると
40°+A=180°
A=140°

これで三角形の二つの角度が分かりました。後は、次のように?を求めるだけです。

15°+140°+?=180°
?=180°−15°−140°=25°

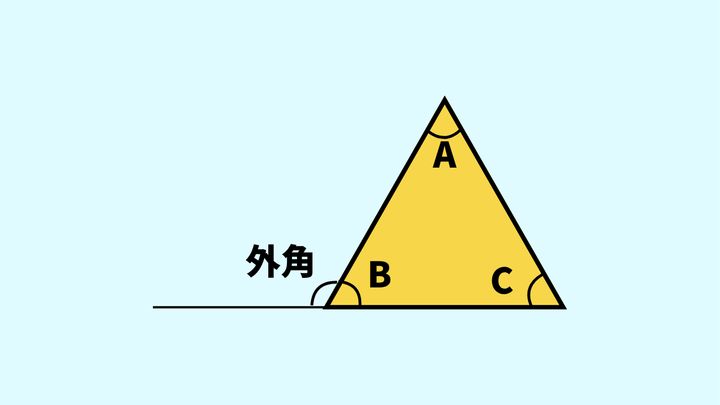
実は、三角形の外角には「外角と隣り合わない二つの内角の合計と大きさが同じ」という性質があります。

この性質が成り立つ理由を考えてみましょう。

「三角形の三つの角の合計は必ず180°になる」のでA+B+C=180°です。また、外角とBの角を足すと一直線が生まれるので外角+B=180°が成り立ちます。この二つの式を比べてみると、A+Cが外角と一致することが分かります。

A+B+C=180°⇔(A+C)+B=180°
外角+B=180°

A+C＝外角

この性質を使って、今回の問題を計算すると、すぐに答えを出すことができますよ。

?+15°=40°
?=25°

計算量が少なくなり、あっさり答えが出せました。

三角形の角度の問題では、内角の合計が180°になることに加えて、この外角の性質も覚えておくと便利ですよ。

今回は、三角形の角度を求める問題にチャレンジしました。

まず、「三角形の内角の合計は180°になること」は、必ず覚えておきたい基礎事項です。この性質さえ知っていれば、三角形の二つの内角が分かっている三角形であれば、もう一つの内角を求めることができます。

中には今回のように、一つの内角しか分かっていないように見える問題もあります。そんなときは、問題図の中から内角の大きさに通じる要素を探してみましょう。今回であれば、外角がもう一つの内角を求める要素になりました。

このような少し応用的な三角形の角度の問題は、数をこなすうちに計算方法が分かってきます。ぜひ、様々な問題にチャレンジしてみてくださいね。

※当メディアでご紹介する数学関連記事において、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。

もう一問挑戦！

これどうやって計算するか覚えてる？「角度が不明な三角形」→この角度は？