これどうやって計算するか覚えてる？「平行四辺形の面積は？」→正しく計算できる？

図形の問題に正解するには、覚えておかなければならない必須の公式がいくつかあります。

この公式は暗記しているだけではなく、問題の中で使いこなせることが大事ですよ。

今回は「平行四辺形の面積の公式」に関する問題にチャレンジしてみましょう。

問題

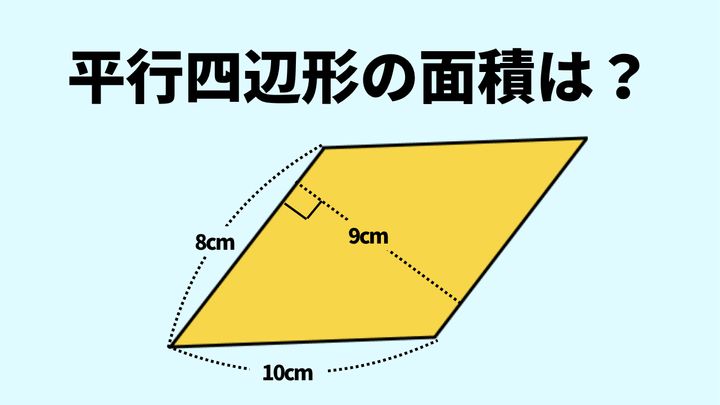
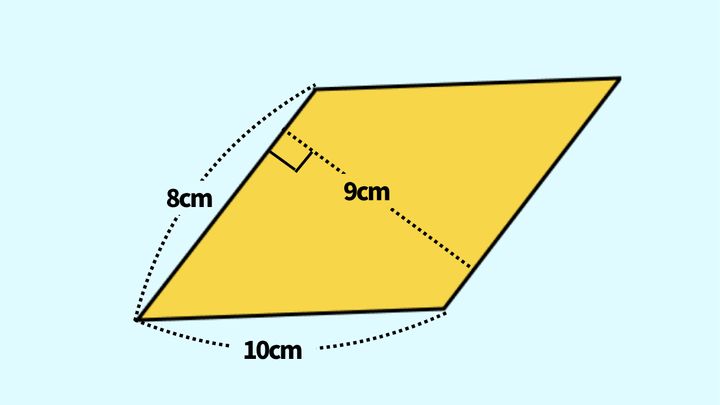
この図形の面積を求めなさい。
※長さや面積の縮尺は、必ずしも正確に描かれていません。

正解は、「72cm2」です。

80cm2と答えてしまった人は、残念ながら間違いです。

平行四辺形の面積の公式を文字として暗記している場合、今回のような問題では誤答する可能性が高くなります。

では、正解するための「ポイント」を確認していきましょう。

この問題のポイントは、「底辺と高さをどこと見るか」です。

まず、平行四辺形の面積の公式をおさらいしてみましょう。

平行四辺形の面積の公式：底辺の長さ×高さ

この公式を丸覚えしていると、「底辺だから底（下）にある辺だな」「高さだから縦の辺だな」と勘違いしてしまう可能性があります。

しかし、底辺は文字通り底にある辺とは限りません。実は、平行四辺形のどの辺でも底辺になりえるのです。

また、高さとは底辺と向かい側の辺との距離のことです。この距離は底辺と垂直に交わる線の長さで表されます。

つまり、平行四辺形の面積の問題では「垂直に交わっている辺同士のペア」を探すことが大事なのです。

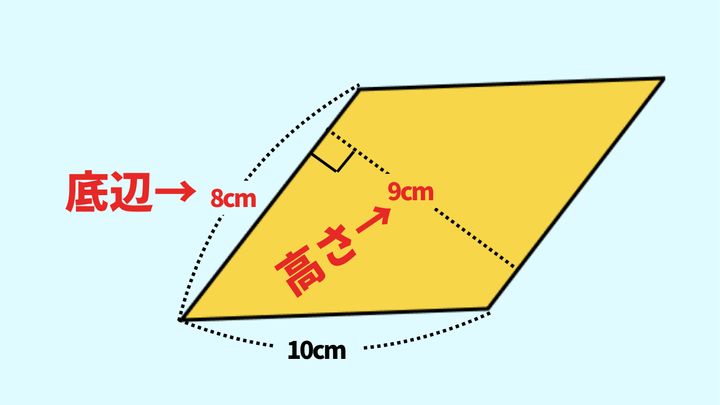
ここで、今回の問題を改めて見てみてください。8cmの辺と9cmの線が垂直に交わっているのが分かりますね。よって、8cmの辺を底辺とし、9cmの線の長さと見ることができます。

後はこれらの数字を公式にあてはめて、計算すればよいですね。

底辺の長さ×高さ=8cm×9cm=72cm2

下にある10cmの辺を底辺、縦の8cmの辺の長さを高さとして計算すると、80cm2と誤答してしまうので注意してくださいね。

なお、この公式の意味は、次のように図形の形を変更すると分かります。

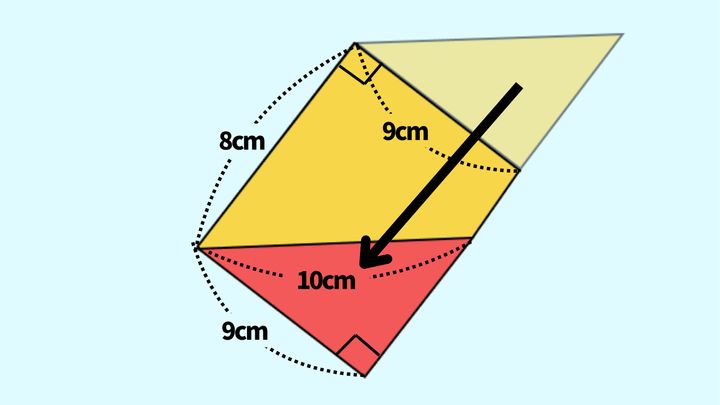
図形を垂直な線（高さを表す線を平行移動したもの）で切って、上にできた三角形を下に移動します。すると角がすべて90°の長方形ができます。

長方形の面積は、縦の辺の長さ×横の辺の長さで求められました。この二つの辺の長さは、平行四辺形の底辺（8cm）と高さ（9cm）に対応しています。

公式の中の底辺や高さという言葉がどの部分を指しているのかが分からなくなったら、このように平行四辺形を長方形に変形してみるとよいでしょう。

今回は、平行四辺形の面積を求める問題にチャレンジしました。

平行四辺形の面積の公式は「底辺の長さ×高さ」で求められます。これは「一辺の長さ×その辺と垂直に交わっている線の長さ」という意味で覚えておくと、使いやすくなります。

底辺や高さという言葉に引きずられて、底辺=下の辺、高さ=縦の辺というような誤解をしないようにしましょう。

※当メディアでご紹介する数学関連記事において、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。

もう一問挑戦！

これどうやって計算するか覚えてる？「この平行四辺形の面積は？」→正しく答えられる？