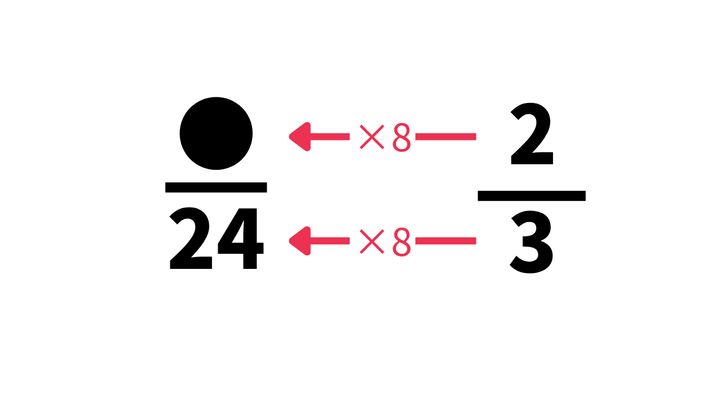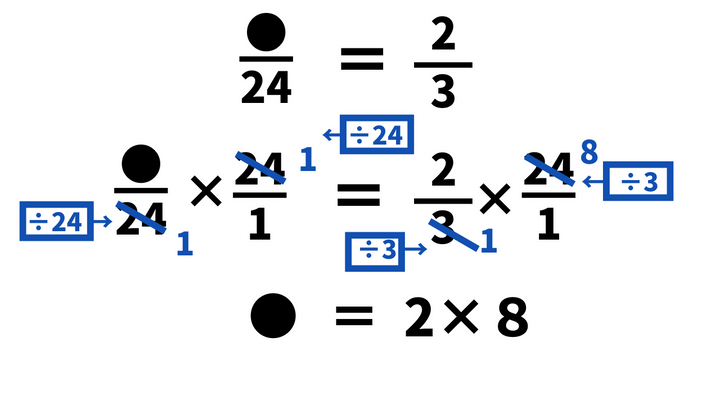意外に間違える人が多いかも…？「●/24=2/3」→●に当てはまるのは？

今回は、「同じ大きさの数を表す分数を求める」問題にチャレンジしてみましょう。

この問題は、分数の足し算や引き算にも通じる「分数の基本」を復習するのにぴったりですよ。

どうやって答えを求めたらよいか、ぜひ自分の頭で考えてみてください。

問題

次の●に当てはまる数を求めなさい。
●/24=2/3

解答

正解は、「16」です。

どうやって答えを出したらよいか悩んだという人は、ぜひ次の「ポイント」を見てください。

この問題はもちろん、分数の計算方法にもつながる分数の性質について解説していますよ。

ポイント

この問題のポイントは、「分数では、分子と分母に同じ数を掛けても、分子と分母を同じ数で割っても大きさは変わらない」という性質です。

言葉では理解しづらいと思うので、次の式を見て具体的なイメージを持ってください。

<例1：分子と分母に同じ数を掛ける>
1/2=(1×3)/(2×3)=3/6
<例2：分子と分母を同じ数で割る>
10/20=(10÷10)/(20÷10)=1/2

では、この性質を利用して、今回の問題を解いてみましょう。

●/24=2/3

二つの分数はイコール関係になるので、●/24は2/3の分子と分母に同じ数を掛ける、あるいは、分子と分母を同じ数で割るかしてできた分数と考えられます。

ここで分母の24と3を比べます。3が24になるには何を掛ければよいかというと、8ですね。つまり、右辺の分数を左辺の分数にするには、分子分母に8を掛ければOKだということです。

右辺の分子は2なので、2×8をすれば●に当てはまる数が分かりますね。

8×2=●
●=16

別解

式の両辺に数を掛けて、分母を消していく方法もあります。

この式であれば、両辺に24/1を掛けてあげれば、分母が消えます。

●/24=2/3
●/24×24/1=2/3×24/1
●=2×8←●=の形になる
●=16

 

分数の掛け算に慣れているという人は、こちらのやり方の方がスムーズに答えを出せるかもしれません。

まとめ

分数では、分子と分母に同じ数を掛けても、分子と分母を同じ数で割っても大きさは変わりません。

この性質は分数の計算にとても役立ちます。

例えば、足し算と引き算では通分をします。通分とは、分子と分母に同じ数を掛けて、二つ以上の分数の分母をそろえることです。また分数の計算結果は約分をすることが多いです。約分とは、分子と分母を同じ数で割って、分数をより簡単な形で表すことです。通分と約分、どちらにもこの問題で登場した分数の性質が活かされていますね。

分数の性質を思い出したという人は、引き続き分数の計算問題にもチャレンジしてみてくださいね。

※当メディアでご紹介する数学関連記事において、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

---

---

文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。

---

もう一問挑戦！