タイル発見者のブログを見つけたのでメモ。

はじめに

非周期的な敷き詰め問題テッセレーションに関する有名な図形として、ペンローズタイルが有名。
ペンローズタイルは２種類の図形が必要で、１種類の図形で同様の特徴を持つ図形がないか探されていた。
で、最近見つかった。

文献

発見者はDavid Smith
文献は２件
Combinatorial Theory誌

①
2023年3月20日　投稿
2023年12月29日　採択
2024年6月30日　出版
タイトル：An aperiodic monotile

もしくは

②
2023年5月29日　投稿
2024年6月7日　採択
2024年9月30日　出版
タイトル：A chiral aperiodic monotile

もしくは

カイラル非周期モノタイル

A chiral aperiodic monotile
このタイルに関する専用サイトは以下

文献①で登場したhat図形では、平面充填するのにオモテとウラを使う必要があった。
文献②では、Tile(1,1)図形が、オモテとウラを使うと周期性が出て、一方のみ使うと周期性が出ないことを明らかにした。
さらに、Spectres図形では、オモテとウラを使っても、一方のみ使っても、周期性が出ないことを明らかにした。

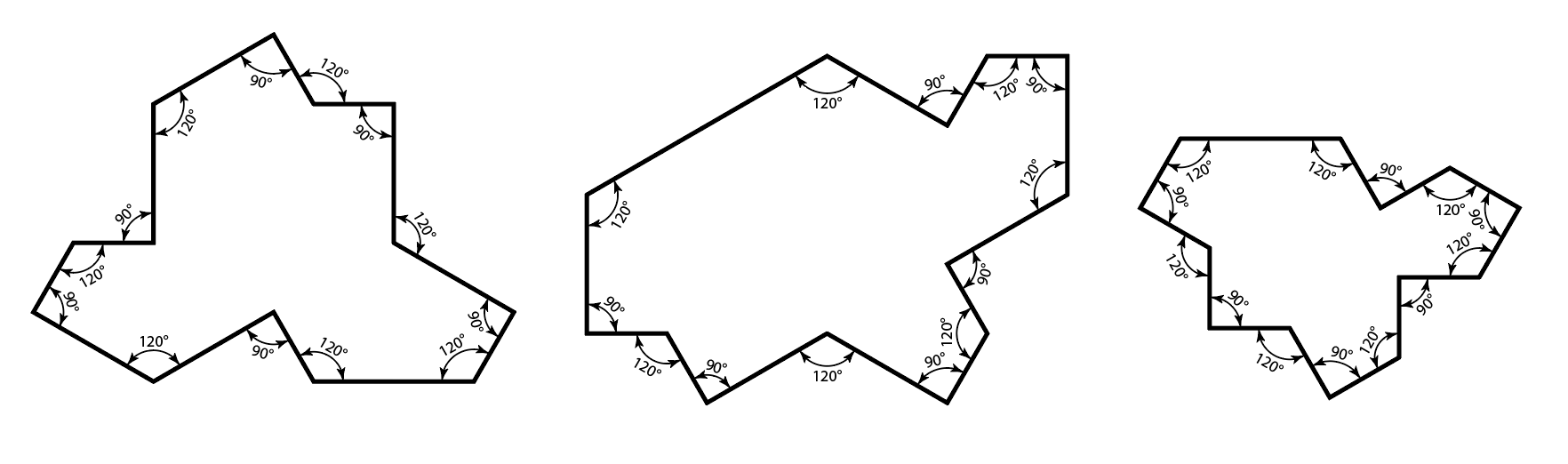
左から hat, turtle, Tile(1,1)
頂点数は13
辺の比は1:√3

論文中にはTile(1,1)をカーブさせたspectresが登場する。
それを私が半円でアレンジしてみたのが以下。
曲率の連続性がないからイマイチ。

my arrange	tiling

発見者のブログ

2016年4月〜2023年8月

2023年9月〜

1つ目のブログには、数多くの充填図形が投稿されていて、発見したという内容は、
2023年3月23日に投稿されている。
それ以前の投稿でも、類似する図形の探求をしている投稿が多数あるので、試行錯誤の過程というか、どんなふうに発見に至ったのか、なんとなく推察できる。

使用ソフトはpolysolver

java環境を整えれば動く