1日たった10秒でできる水虫治療法とは？水虫の人絶対やって
PR(株式会社アルトルイズム)
ひし形の面積の公式は、小学校の算数で学習します。
しかし、大人になると計算の方法を忘れていないでしょうか。
ここでは、ひし形の面積の求め方と、なぜこのような公式になるのかを解説します。
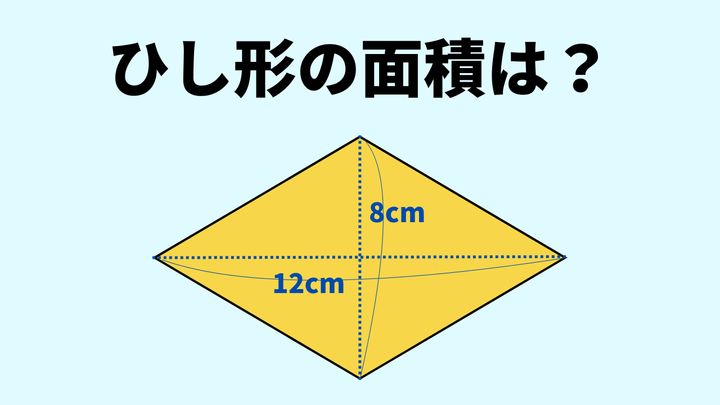
問題
次のひし形の面積を求めなさい。
ひし形の面積はどのように計算すればいいのでしょうか。
正しく答えを求めてみましょう。
解説
今回の問題の答えは「48(cm2)」です。
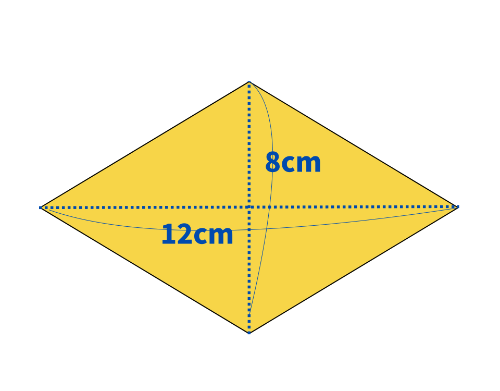
問題のひし形は、対角線が8cm、12cmなので、次のように計算ができます。
ひし形の面積
=対角線×対角線÷2
=8×12÷2
=48
公式を覚えていれば、簡単な計算になりますね。
ひし形の面積の公式
ひし形の面積の公式は、「対角線×対角線÷2」です。
しかし、なんとなくうろ覚えで「÷2」が必要なのか、必要ないのかで迷った方もいるのではないでしょうか。
このひし形の面積に関する公式は、次のように求められます。
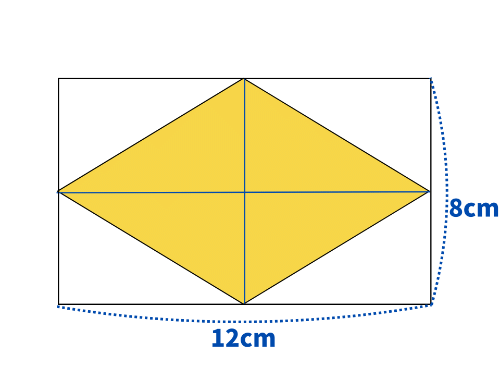
長方形のそれぞれの辺の中点（真ん中）を結ぶとひし形になります。
さらに縦と横の線を入れると、上図のように8個の合同な三角形になります。
そのうち、ひし形は「三角形4つ分」の面積です。
つまり、ひし形は「長方形の半分」となります。
このように計算できることを知っていると「÷2」が必要であることは簡単に分かりますね。
まとめ
公式は丸暗記するのではなく「なぜそうなるのか」を考えると、忘れにくくなるでしょう。
ぜひ他の記事の問題にも挑戦し、正しい理解ができているか確認をしてみてください！
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。
あくまでも一例のご紹介に留まることを、ご了承ください。
文（編集）：SAJIMA
日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」
類似問題に挑戦！
