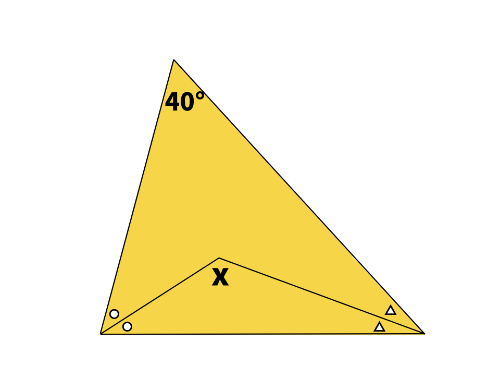
図形の角度を求める問題に挑戦してみましょう。
図形の問題と言っても、「計算力」も求められます。
正しく求めることができるでしょうか。
問題
次のxの角度を求めなさい。ただし、同じ記号のついた角はそれぞれ等しいとする。
分かっている角度は「40°」の一か所だけです。
どのように求めれば良いのでしょうか。
解説
今回の問題の答えは「110°」です。
どのように求めるのか順に解説をしていきます。
解説のため、下図のようにA,B,C,Dとする。また「◯の角」の大きさはa、「△の角」の大きさはbと表す。
まずは、三角形ABCに着目します。
三角形の内角の和は180°なので、
角BAC+角ABC+角ACB =180
つまり
40+2a+2b=180
この等式を変形します。
2a+2b=180-40
2a+2b=140
a+b=70
次に、三角形DBCにおいて、同様に考えます。
角BDC+角DBC+角DCB =180
つまり
x+a+b=180
ここで、先ほど求めた「a+b=70」を代入します。
x+70=180
x=110
したがって、答えは「110°」となります。
「三角形の内角の和は180°」という性質から、等式を作り、正しい式変形をすることで、答えを求めることができましたね。
まとめ
今回の問題は、中学生で学習するものです。
図形の性質と等式の計算を正しく理解していなければ解けません。
忘れていた方は、ぜひ復習をしてみると良いでしょう。
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。
あくまでも一例のご紹介に留まることを、ご了承ください。
文(編集):SAJIMA
日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」
もう1問挑戦!