どうやって計算するか覚えてる？「三角形の外角」→この角度は？

図形の問題を解くには、図形に関する様々な特徴を覚えている必要があります。

今回の問題にチャレンジすると、三角形の角に関する基本を確認できますよ。

懐かしいこの問題、あなたは正しく答えられるでしょうか？

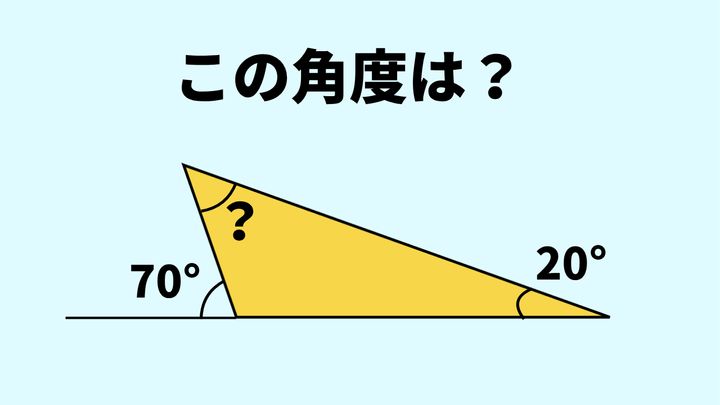
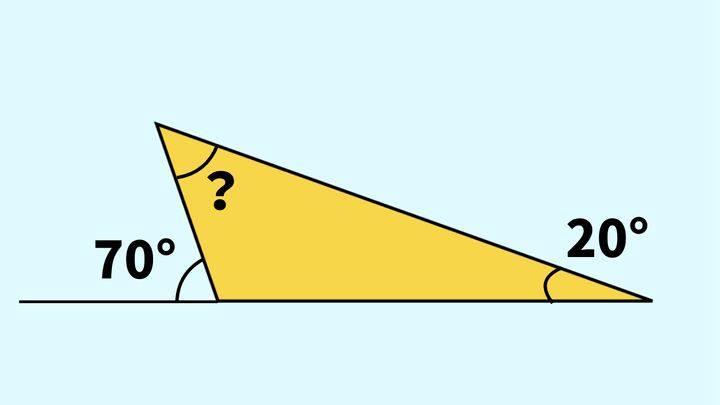
問題

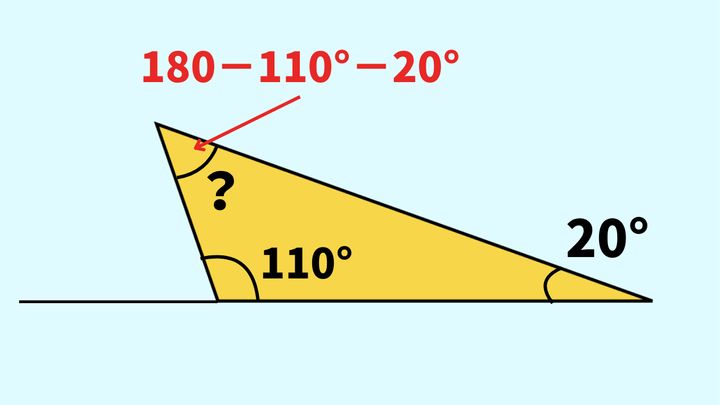
?に当てはまる角度を求めなさい。

正解は、「50°」です。

分かっている角の大きさをどのように組み合わせて計算したら、この答えにたどり着けるのでしょうか。

次の「ポイント」で、三角形の角に関する基本と、計算手順を確認してみましょう。

この問題のポイントは、「三角形の三つの角の大きさを合計すると180°になる」ことです。

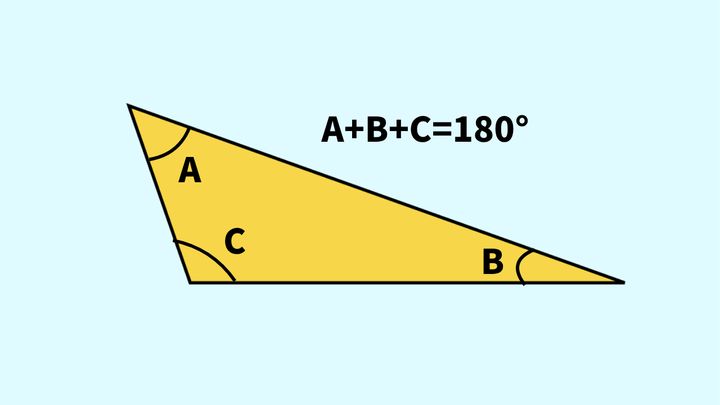
三角形の角（内角）の大きさをそれぞれA、B、Cとすると、
A+B+C=180°

しかし、今回の問題では、三角形の三つの角のうち、20°という一つの角の大きさしか分かっていません。

そこで、70°を手掛かりに、もう一つの角の大きさを求めていきましょう。

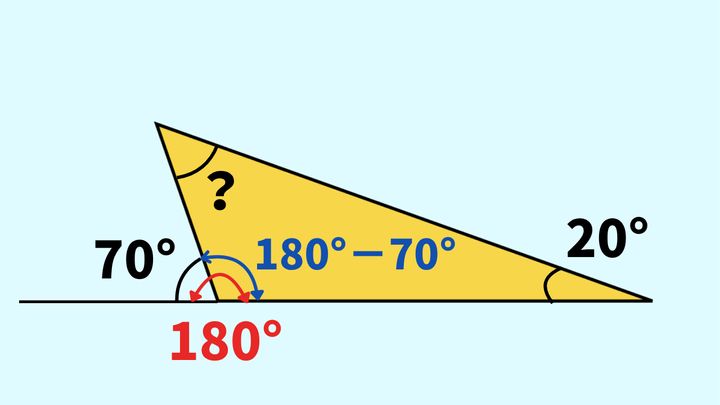
70°は、三角形の一辺を延長した線と隣の辺との間にできています。このような角は、三角形の中にある内角と区別して、外角と呼びます。

外角と隣り合う内角を足すと、一直線になりますので、ちょうど180°になります。つまり、180°−70°を計算すると、三角形の内角を求めることができるのです。

70°+隣り合う内角=180°
180°−70°=隣り合う内角=110°

これで、二つの内角110°と20°が分かりました。この二つの角と?を足すと、180°になります。

110°+20°+?=180°

?を求めるには180°から110°と20°を引けばよいですね。

180°−110°−20°=50°

これで答えが求められました。

実は、この問題には別解があります。

三角形の外角には、次のような性質があります。

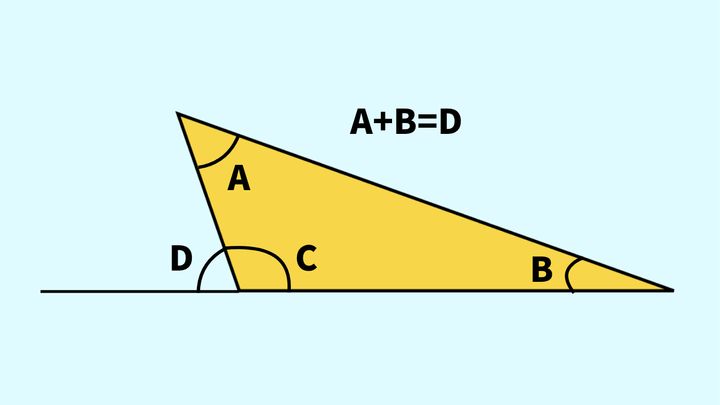
三角形の外角は他の二つの内角を足したものと同じ大きさになる

三角形の内角の性質から「A+B+C=180°」、そして一直線なので「D+C=180°」も言えますね。つまり、「A+B+C=D+C」なのです。また両辺を見るとCは共通しているので、A+B=Dも言えるというわけです。

A+B+C=180°
D+C=180°

A+B+C=D+C
A+B（C以外の二つの内角を足したもの）=D（外角）

ここで改めて、今回の問題を見てみましょう。

外角70°は?と20°の合計と等しいので、次のように計算ができます。

?+20°=70°
?=70°−20°=50°

外角と内角の関係を使うと、より簡単に答えを出せますね。

今回は、三角形の角度を求める問題にチャレンジしました。

「三角形の三つの角（内角）の大きさを合計すると180°になる」ことは、図形問題を解く上での基本知識です。また、「三角形の外角は他の二つの内角を足したものと同じ大きさになる」ことも覚えておくと便利ですよ。

この知識を活かして、いろいろな三角形の問題にチャレンジしてみてくださいね。

※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。

類似の数学問題にもう1問挑戦！

これどうやって計算するか覚えてる？「三角形の2つの内角がそれぞれ78°と32°」→残りの角度は？