大人が意外と間違える数学「43×37」→暗算できる？

皆さんは、「2桁×2桁」の掛け算をどのように解いていますか？

数字によっては暗算で簡単にできることもありますが、多くの人は電卓に頼ってしまうのではないでしょうか。

でも、「インド式計算法」を使えば、誰でも素早く暗算で解くことができるんです。

思考力が詰まった「インド式計算法」で、楽しく計算力を鍛えましょう！

問題

次の計算を暗算でしなさい。
43×37

「インド式計算法」を知っていれば、一瞬で答えを出せてしまいます。

やり方をまだ知らない方は、まずは通常の方法で計算してみてください。あとからご紹介する「インド式計算法」と比べると、その計算スピードの差にきっと驚くはずです。

解説

今回の問題の答えは「1591」です。

ここでは、「インド式計算法」を使った解き方をご紹介します。

この計算法では、「どんな形の数同士を掛けているか」によって、使う解法が異なります。

今回は、次の条件を満たすときに使えるパターンです。

掛け算する2つの数が、「10の倍数にある数を足したもの」と「同じ数を引いたもの」になっている

「43×37」では、
43=40+3
37=40−3
となり、「40」を基準に、「3」を足した数と引いた数になっているのがポイントです。

このようなときは、次の手順で解きます。

【手順1】
基準とした数（今回は40）を2乗する
40×40=1600

【手順2】
足したり引いたりした数（今回は3）を2乗する
3×3=9

【手順3】
手順1の結果から、手順2の結果を引く
1600−9=1591

とてもシンプルに計算できましたね。

慣れてくれば、暗算で一瞬で求められるようになりますよ。

計算が成り立つ理由

ではなぜこの計算方法で正しい答えが出るのでしょうか？

知らなくても使えますが、理由を理解しておくと、計算ミスを減らすことができます。

ここでは、2つの方法でその仕組みを解説します。

展開公式を使う

今回の方法は、中学校で学ぶ「展開公式」のひとつに基づいています。

(a+b)(a-b)=a^2-b^2

この公式に当てはめると、

(40+3)(40-3)
=40^2-3^2
=1600-9
=1591

となり、先ほどと同じ正解が導かれます。

面積図を使う

中学数学が苦手な方も、小学校までの知識で仕組みを理解できます。

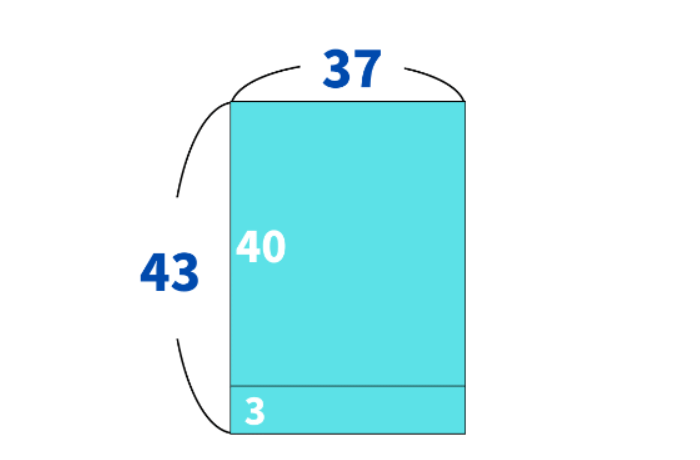
「43×37」の計算は、縦43cm・横37cmの長方形の面積を求めることと同じです。

この長方形を、図のように2つに分けてみましょう。

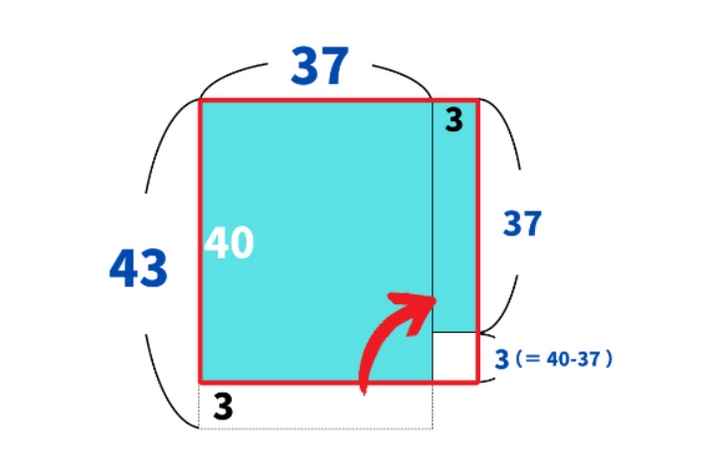
次に、「3×37」の細長い長方形を、向きを変えて配置し直します。

そうすると、縦の長さは「40（=43−3）」になり、横の長さも「40（=37+3）」になります。

つまり、「40×40」の正方形ができ、計算がとても楽になります。

ただし、注意が必要なのは右下の部分。縦の長さが足りていないため、白い空白ができます。この部分を引く必要があります。

この白い部分は、「3×3」の正方形です。

したがって、面積の計算は次のようになります。

「40×40」の正方形（赤い太枠）
→1600cm2（手順1）

「3×3」の正方形（白い部分）
→9cm2（手順2）

求めたい面積（水色の部分）
→1600−9=1591cm2（手順3）

今回は「43×37」の計算で説明しましたが、次のような条件を満たす掛け算なら、同じ方法が使えます。

掛け算する2つの数が、それぞれ「10の倍数にある数を足したもの」と「同じ数を引いたもの」になっている

まとめ

「インド式計算法」は、繰り返し練習すれば誰でも使いこなせるようになります。

ただし、すべての計算がこの方法で解けるわけではないので、「どんなときに使えるか」を見極めることが大切です。

今回ご紹介したパターン以外の方法は、別の記事で詳しく解説しています。ぜひそちらもご覧ください。

※当メディアでご紹介する数学関連記事では、複数の解法がある場合もあります。本記事の内容はあくまで一例としてご紹介しています。ご了承ください。

---

文・編集（監修）：SAJIMA
日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」