これどうやって計算するか覚えてる？「台形の面積を求めなさい」→正しく計算できる？

今回は図形の面積を求める問題に挑戦してみましょう。

さまざまな図形がありますが、公式が少し長い台形に注目します。公式だけでなく、その成り立ちまでしっかりと復習することで定着率が大きく変わります。

頭を柔らかく視覚的に捉えていきましょう。

問題

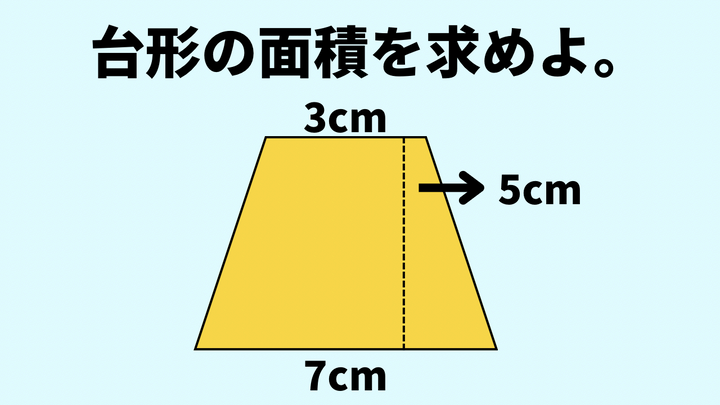
上の図の台形の面積を求めなさい。

台形の面積公式を覚えるために、その成り立ちも考えてみましょう。

この問題の答えは「25cm2」です。

単位に注意してみてください。

早速、台形の面積を求める公式を思い出していきましょう。

＜台形の面積の公式＞
台形の面積=(上底+下底)×高さ÷2

一旦、この公式に当てはめて計算してみます。

面積
=(3+7)×5÷2
=10×5÷2
=50÷2
=25

では、どうしてこの公式で台形の面積を求めることができるのでしょうか。

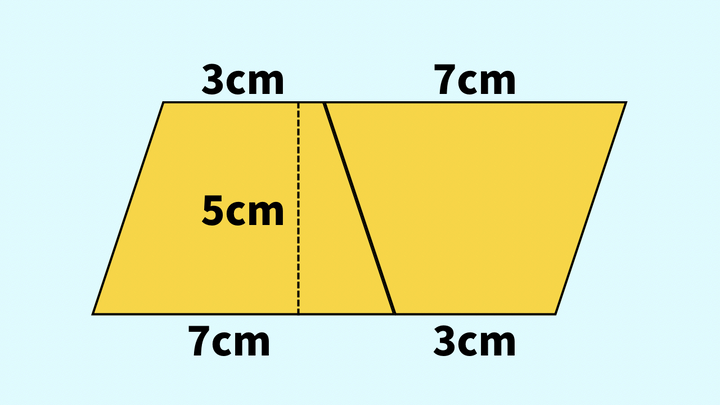
公式の成り立ちを考えるために、同じ台形をもう一つ用意して下の図のようにくっつけてみてください。

すると、平行四辺形が完成しました。平行四辺形の面積÷2をすることで台形一つ分の面積を求めることができます。

＜平行四辺形の面積の公式＞
平行四辺形の面積=底辺×高さ

この「底辺」に当たる部分を分割して捉えると、

平行四辺形の底辺=台形の(上底+下底)

であることが分かりますね。

このことから、底辺を(上底+下底)として最後に2で割ることで、台形の面積公式が成り立ちます。

今回は公式を覚えるために成り立ちから復習しました。どんどん遡って、今度は平行四辺形の面積の成り立ちが気になりませんか？

実は平行四辺形の面積は長方形の面積の公式から考えることができます。

そんな簡単なところから繋がっている数学はちょっぴり神秘的ですね。

※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

文（編集）：うおうお
数学の教員免許を所持。個別指導・集団指導の学習塾で数学の講師として小学生から高校生までの指導や、小学生の宿題指導を通して算数の魅力を深堀して楽しく伝えている。現在は民間学童保育所で放課後児童支援員として勤務しながらフリーランスで受験指導もしている。

もう一問挑戦！

意外に間違える人が多いかも…？「台形の面積は？」→正しく答えられる？