これどうやって計算するか覚えてる？「台形の面積は？」→正しく答えられる？

小学校で習った台形の面積の公式を覚えていますか？

細かい公式の内容は忘れてしまった、という人でも大丈夫。

台形の特徴さえ思い出せれば、他の図形の面積の公式を利用して答えを求めることもできますよ。

問題

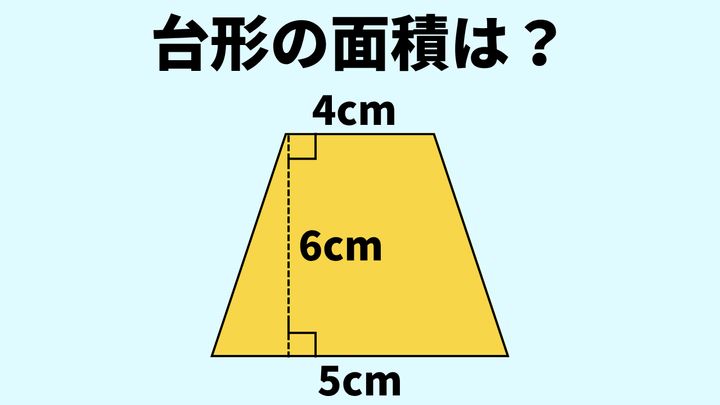
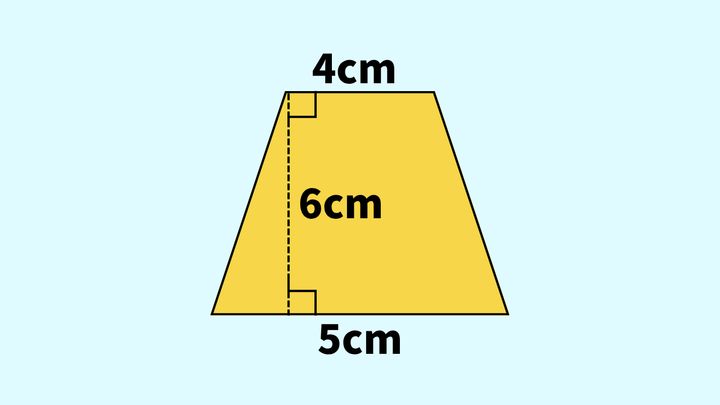
次の台形の面積を求めなさい。

解答

正解は、「27cm2」です。

台形の面積の公式は、「(上底+下底)×高さ÷2」です。

この問題でいえば、上底=4cm、下底=5cm、高さ=6cmなので、次の式で答えが求められます。

(4+5)×6÷2=27

台形の面積の公式は三角形や平行四辺形の面積の公式に比べてちょっと複雑で、忘れてしまっていたという人もいるかもしれません。

しかし、もしこの公式を忘れても、他の面積の公式を覚えていれば台形の面積を求めることは難しくないのです。

次の「ポイント」で、さまざまな台形の面積の求め方を見てみましょう。

ポイント

公式を忘れてしまったときに台形の面積を求めるには「台形を切ったり、くっつけたりして別の図形にすること」がポイントになります。

こうすれば他の図形の面積の公式を利用して、答えを求めることができます。

方法1：二つの三角形に分けて計算する

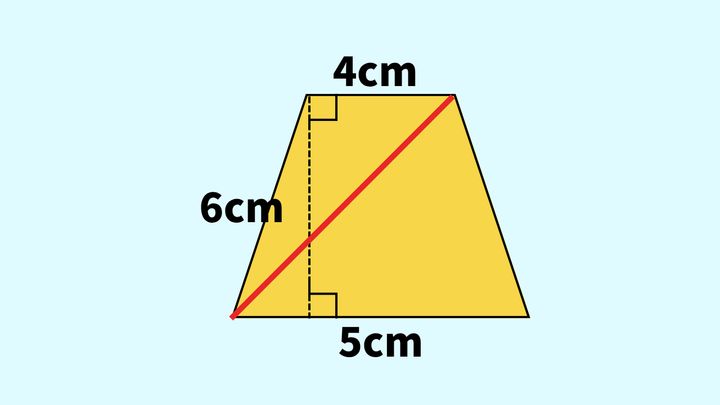
まずは、対角線で台形を二つの三角形に分ける方法を考えてみましょう。

上の三角形は底辺4cmで高さ6cm、下の三角形は底辺5cmで高さ6cmです。三角形の面積の公式は「底辺×高さ÷2」ですから、次のように計算ができます。

上の三角形の面積：4cm×6cm÷2=12cm2
下の三角形の面積：5cm×6cm÷2=15cm2

あとは、この二つの面積を足すと台形の面積が求められます。

12cm2+15cm2=27cm2

台形の上底と下底は平行なので、二つの三角形の高さは台形の高さと同じになるところがポイントです。

ちなみに、上の三角形の底辺は台形の上底にあたり、下の三角形の底辺は台形の下底にあたります。よって、二つの三角形を足して台形の面積を求める式は、台形の面積の公式につながっていることが分かります。

上の三角形の面積：上底×台形の高さ÷2
下の三角形の面積：下底×台形の高さ÷2

上の三角形の面積+下の三角形の面積
=上底×台形の高さ÷2+下底×台形の高さ÷2
=(上底+下底)×台形の高さ÷2
=台形の面積の公式

方法2：平行四辺形にして計算する

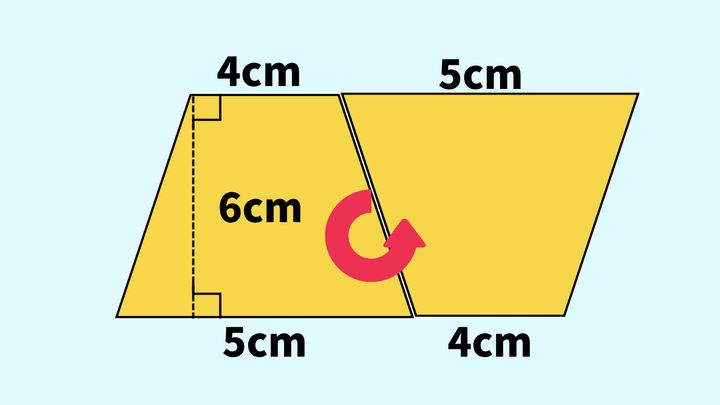
次に紹介する方法は、台形二つを組み合わせて平行四辺形を作る方法です。

台形をコピーして上下を反対にし、元の台形とくっつけると平行四辺形ができます。

まずは平行四辺形の面積の公式「底辺×高さ」を利用して、この平行四辺形の面積を求めます。平行四辺形の底辺の長さは、元の台形の下底5cmとひっくり返した台形の上底4cmを足せば求められますから、計算は次のようになります。

(5cm+4cm)×6=54cm2

54cm2は台形二つ分の面積なので、これを2で割れば台形一つ分の面積が求められます。

54cm2÷2=27cm2

実はこの計算過程も、台形の面積の公式につながっています。以下の式を見てください。

台形二つでできる平行四辺形の面積=(台形の上底+下底)×台形の高さ

台形二つでできる平行四辺形の面積÷2
=(台形の上底+下底)×台形の高さ÷2
=台形の面積の公式

まとめ

今回は、台形の面積を求める問題にチャレンジしてみました。

小学校のときに習った「(上底+下底)×高さ÷2」の式を覚えていれば一発で答えが出る問題ですが、仮に忘れてしまっていても、三角形や平行四辺形の面積の公式を利用して解答することもできます。さらにいえば、三角形や平行四辺形を利用して台形の面積を求めることは、台形の面積の公式の成り立ちを知ることにもつながります。

算数の公式の裏には、その公式が成り立つだけの理由があります。その理由さえ理解できていれば、公式そのものを忘れてしまっていても答えを出すことができますよ。

※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

---

---

文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。

---

もう一問挑戦！