これどうやって計算するか覚えてる？「10÷0.5」→正しく計算できる？

今回は、割る数が小数の問題に挑戦してみましょう。

昔習った小数の割り算の計算方法を思い出せなくても大丈夫！式の意味を考えることでも、答えが出せますよ。

自由な発想で計算してみてください。

問題

次の計算をしなさい。
10÷0.5

まずは割り算の意味について、考えてみましょう。

解答

正解は、「20」です。

割り算なのに答えが「割られる数の10」よりも大きくなるのは、なんだか不思議な感じがするかもしれません。

では、今回の問題はどのように計算したらよかったのか、次の「ポイント」で確認してみましょう。

ポイント

今回は、「割り算のイメージを使う」「割り算を分数に直す」、二つのポイントに注目して計算する方法をそれぞれ紹介します。

割り算のイメージを使って計算

最初に、割り算のイメージを使う計算方法を見てみましょう。

割り算は、「一人あたりにある数ずつ分けると、何人分になるか求めるとき」に使える計算です。

例えば、10÷5は10個のクッキーを一人当たり5個ずつに分けるとき、何人に分けられるか求める式だといえます。

10÷5=2

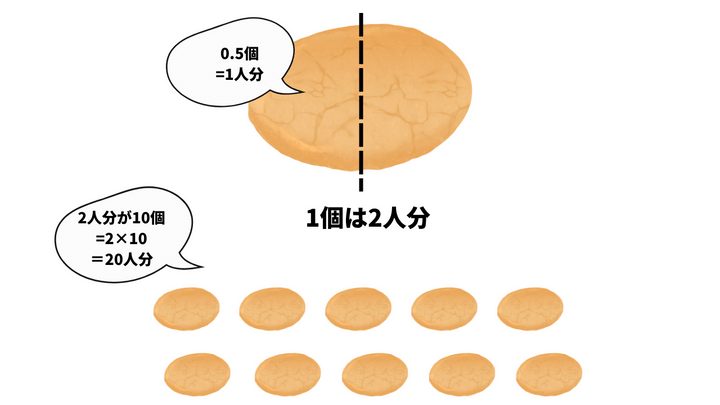
同じように考えると、今回の問題の式10÷0.5は10個のクッキーを一人当たり0.5個ずつに分けるとき、何人に分けられるか求める計算だと考えられます。

0.5は1の半分ですから、クッキー1個は2人分になります。このクッキーが10個あるのだから、答えは10×2=20（20人に分けられる）です。

これで、この問題の答えは20だと分かります。

10÷0.5=20

 

分数に直して計算

次に、分数に直して計算してみましょう。

a÷bの割り算は、a/bという形の分数に直せます。

10÷0.5
=10/0.5

分数は分子と分母に同じ数を掛けても大きさは変わりません。そこで、分子と分母に10を掛けてみましょう。

10/0.5
=(10×10)/(0.5×10)
=100/5

これをもう一度割り算に直すと、見慣れた整数÷整数の式ができます。

100/5
=100÷5

あとはこれを整数の割り算として計算するだけです。

100÷5
=20

これで答えが出ましたね。

学校で習う計算ルール

ちなみに、学校で習う「割る数が小数のときの計算ルール」は以下の通りです。

<割る数が小数のときの計算ルール>

ステップ1：割る数が整数になるまで10の倍数を掛ける
ステップ2：割られる数にもステップ1と同じだけ10の倍数を掛ける
ステップ3：割り算をする

この計算ルールに従うと、次のように計算ができます。

10÷0.5
=(10×10)÷(0.5×10)←ステップ1、2
=100÷5←ステップ3
=20

先に紹介した「割り算を分数に直す方法」とやっていることはほぼ同じだと分かりますね。

まとめ

今回は、「割る数が小数の計算問題」について、二つの答えの出し方を紹介しました。

小数の割り算の仕方は小学校で習いますが、日常ではあまり使わないため、大人になってから計算しようとすると戸惑ってしまうことも多いでしょう。

なかなか計算ルールを思い出せないときは、割り算の意味や他の計算のルールを応用して答えが出せないかを考えてみてください。子ども時代には気が付かなかった新しい観点に気づくきっかけになるかもしれませんよ。

懐かしい計算問題は他にも用意していますので、引き続き挑戦してみてくださいね。

※当メディアでご紹介する数学関連記事において、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

---

---

文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。