この数式を完成させられる？「10000÷□÷25=100」→□に当てはまるのは？

今回は、□に当てはまる数を求める問題です。

あてずっぽうで数字を入れていく前に、式に現れているほかの数字をしっかり確認することをおすすめします。

式の右辺と左辺を見比べることで、答えに近づけますよ。

問題

□に数を入れて、数式を完成させてください。
10000÷□÷25=100

登場する数字の大きさに惑わされずに、冷静に式を観察してみましょう。

正解は、「4」です。

どうやって答えを求めたらよいか、分かったでしょうか？

次の項で、考え方の「ポイント」を確認してみましょう。

今回の問題では、「二つの割り算を一つの割り算として考えること」がポイントになります。

10000÷□÷25=100

10000が100になるような割り算といえば、「10000÷100」ですね（÷100をすると位が二つ下がります）。

では、もとの式と「10000÷100」を比べてみましょう。

10000÷□÷25=100
10000÷100=100

「÷□÷25」の部分が「÷100」と同じになれば、この数式が成り立つことが分かります。

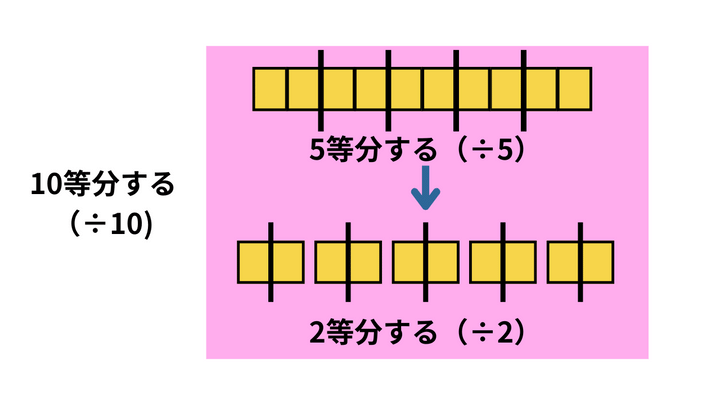
ここで、二つの割り算を一つの割り算ととらえてみます。例えば、「÷5÷2」は、5等分したものをさらに2等分するということです。結果的に元の数は「5×2=10等分」されます。

このようにaで割ってからbで割る二つの割り算「÷a÷b」は、a×bで割る一つの割り算「÷(a×b)」と同じ意味になります。

今回は「÷□÷25」という二つの割り算が、「÷100」という一つの割り算と同じになれば等式が成り立ちます。

つまり、□×25=100となるような□を求めればよいのです。

25を掛けて100になる数といえば、4ですね。

10000÷□÷25=100
10000÷4÷25=100⇔10000÷100=100

念のため「10000÷4÷2」5を順番に計算して、答えが100になるのを確かめてみましょう。

10000÷4÷25
=2500÷25
=100

間違いなく、答えは100になりましたね。

今回は、二つの割り算を一つとみることで、□に当てはまる数を求める方法を紹介しました。

二つの割り算「÷a÷b」は、「a×b」で割る一つの割り算「÷(a×b)」と同じになります。この変換方法は、二つの割り算を効率的に計算するときにも便利に使えることがあります。

例えば、次の問題ではこの手法を使って計算を楽にしていますよ。

興味のある人は、ぜひ挑戦してみてください。

※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。

類似問題に挑戦！

小学生でも分かる問題に挑戦！「8□4□4=6」→正しい計算式を作れる？