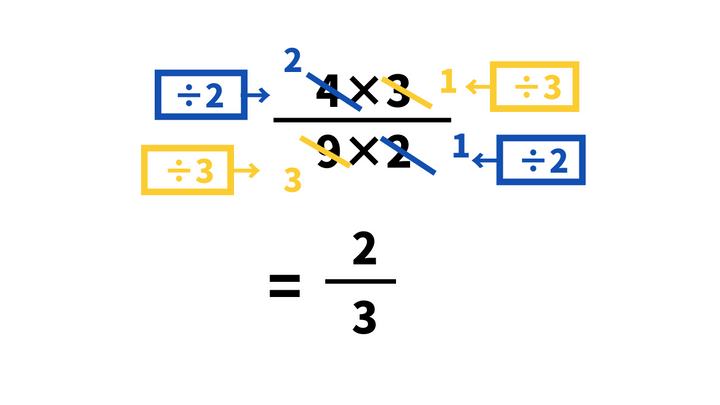小学生でも分かる問題にチャレンジ！「4/9÷2/3」→正しく計算できる？

今回の計算問題には、懐かしの「分数の割り算」が登場です。

小学校のテストや宿題でよく出題されていた思い出の問題ですが、久しぶりに計算しようとするとちょっと戸惑ってしまうかもしれませんね。

自信がある人もそうでない人も、ぜひチャレンジしてみてください。

問題

次の計算をしなさい。
4/9÷2/3

正解は、「2/3」です。

すらすら計算できたでしょうか？

「分数の割り算ってどうやってするんだっけ？」と思考がストップしてしまった人は、ぜひ次の「ポイント」をご覧ください。

分数の割り算のポイントは、「割る数の分子と分母を逆にして掛けること（割る数を逆数にして掛けること）」です。

今回の問題では、割る数は2/3です。この数の分子と分母を逆にすると、3/2（2/3の逆数）ですから、式は次のようになります。

4/9÷2/3
=4/9×3/2

割り算が掛け算の式になりました。分数の掛け算では、分子どうし、分母どうしを掛ければOKです。

4/9×3/2
=(4×3)/(9×2)
=12/18

ですが、これだと答えの「2/3」という形になりませんね。理由は、約分をしていないからです。

約分とは「分子と分母を同じ数で割って、より簡単な形で分数を表すこと」です。
※分数では、分子と分母を同じ数で割っても、表している数の大きさは変わりません。

分数の計算問題では、これ以上約分ができない形で答えを出すのが一般的になっています。

12/18であれば、分子と分母を6で割って約分すると…答えは2/3になりますね。

12/18
=(12÷6)/(18÷6)
=2/3

なお、分数の掛け算では、次のように掛け算前の約分も可能です。

(4×3)/(9×2) ←4と2、3と9を約分
=(2×1)/(3×1)
=2/3

計算が簡単になりますので、できるだけ「掛け算前に約分する」ことをおすすめします。

今回の問題では、分数の割り算に挑戦しました。

分数の割り算では、割る数の分子と分母を逆にした数（逆数）を割られる数に掛けます。つまり、割り算を掛け算に変換して計算するのです。

なお、分数の掛け算をするときには、掛け算前に約分できそうなところを先に約分してしまうのがおすすめです。

久しぶりの小学校の計算問題は、いかがでしたか？
難しかったという人は、もう少し計算クイズにチャレンジしてみてはいかがでしょうか。計算をする中で、昔の勉強の記憶が徐々によみがえってくるはずです。

※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。

もう一問挑戦！

小学生でも分かる問題にチャレンジ！「3.3×10/11÷2.7」