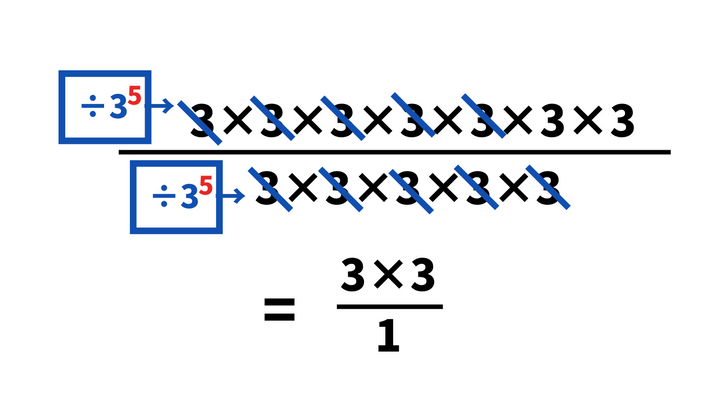今回は、累乗の割り算に挑戦しましょう。
累乗とは、「同じ数を何回か掛けたもの」のことです。実は、ある条件のもとでは、累乗の割り算はとても簡単にできるのです。
さて、今回の問題、あなたは10秒以内に計算できるでしょうか。
問題
次の計算をしなさい。
3^7÷3^5
※制限時間は10秒です。
※3^7は3の7条を表しています。
解答
正解は、「9」です。
「3^7」や「3^5」を計算してから割り算をするとかなり時間がかかってしまいます。
では、どのようにすれば簡単に答えが出せるのでしょうか。
次の「ポイント」で確認してみましょう。
ポイント
この問題では、「割られる数も割る数も3の累乗」であることに注目するのがポイントです。
まずは、累乗とは何かを確認しておきましょう。
累乗とは
累乗とは、「同じ数を何回か掛けたもの」です。掛ける回数は、指数という数で表します。
指数は、掛ける数の右上に小さく書くのが一般的ですが、上付き文字が使えないテキストや表計算ソフトでは「^」を使って指数を表すことがあります。
この記事では、「^」を使って指数を表します。
例えば、「3^2」は、掛ける数は3、指数は2ですので、式の意味は「3を2回掛ける」です。なお、「3^●」の形をしている累乗をまとめて、3の累乗と呼びます。
3^2
=3×3
=9
ここで、今回の問題を見てみましょう。
3^7÷3^5
「3^7」は3を7回掛けたもの、「3^5」は3を5回掛けたものです。累乗は割り算よりも先に計算するため、式全体の意味は、「3を7回掛けた数」÷「3を5回掛けた数」になります。
掛ける数が同じ累乗の割り算
ここまでの内容で式の意味は分かりましたが、「3^7」や「3^5」を直接計算してから割り算するのは時間がかかります。
ここで注目したいのが、割られる数、割る数がともに3の累乗であることです。「掛ける数が同じ累乗の割り算」では、分数形式で考えると計算が早くなります。
「a÷b」の割り算はa/bという分数で表せますので、まずは「3^7÷3^5」を分数にしてみましょう。
3^7÷3^5
=3^7/3^5
次に、分子と分母を3の掛け算の形に直します。
3^7/3^5
=(3×3×3×3×3×3×3)/(3×3×3×3×3)
ここで、「分数の分子と分母は同じ数で割って約分ができる」ことを思い出してください。分子と分母にある3のペアを一つずつ「÷3」をしていくと、分母側に3が二つだけ残ります(分子と分母の数を同じ3^5で割った形になります)。
(3×3×3×3×3×3×3)/(3×3×3×3×3) ←分子も分母も3^5(3を5回掛けたもの)で割る
=(3×3)/1
あとはこれを計算して、整数に直せばおしまいです。
(3×3)/1
=9/1
=9
とても簡単に答えが出せましたね。
この考え方を一般化したルールがこちらです。
aが0ではなく、mもnも整数のとき
a^m÷a^n=a^(m−n)が成り立つ
今回の問題にこのルールを使うと、次のように計算がシンプルになります。
3^7÷3^5
=3^(7−5)
=3^2
=3×3
=9
まとめ
今回の問題は、いかがでしたか?
累乗の計算は数が大きくなりがちですが、累乗に関する計算ルールを使いこなすと、案外あっさり答えが出るケースも多くあります。
今回のように掛ける数が同じ累乗どうしの割り算であれば、「3^7」や「3^5」を直接計算せずに、指数どうしの引き算という形で割り算を処理した方が効率的です。
他にも累乗の計算問題を用意していますので、ぜひ挑戦してみてくださいね。
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。
文(編集):VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。
類似問題に挑戦!