「血糖値が下がらない…」医師も愛用している血糖値対策がすごい！
PR(オーキ製薬株式会社)
今回は、数学でおなじみの「累乗」の計算に挑戦です。
一見ややこしそうに見えるかもしれませんが、あるポイントに注目すれば、即答することも可能な問題ですよ。
さて、あなたは5秒以内に答えが出せるでしょうか。
問題
次の計算をしなさい。
(−1)^99
※制限時間は5秒です。
解答
正解は、「−1」です。
どうすればこの答えにたどり着けるのか、そして5秒以内に素早く計算するにはどうすればよいのか、秘密は式の中の「99」という数字にあります。
では、計算の「ポイント」を、次の項で確認してみましょう。
ポイント
この問題のポイントは、「指数に注目すること」です。
指数とは、「同じ数を何個掛けるか」を表したものです。
例えば、「2^4」という式は、「2を4個掛ける」という意味です。この式の指数は4です。
2^4 ←指数（掛ける個数）は4
=2×2×2×2
※指数は通常掛ける数の右上に小さく書きますが、表計算ソフトや上付き文字の使えないテキストでは「^」の記号を使って指数を表すこともあります。この記事でも「^」で指数を表しています。
なお、「2^4」のように、同じ数を掛けたものを累乗といいます。
今回の問題も累乗の計算問題です。
(−1)^99
先ほどの「2^4」の例を見た人なら、この式の指数は99だと分かりますね。よって、式の意味は「−1を99個掛ける」です。
さて、これをどのように計算すればよいのでしょうか。
先の「2^4」のように掛ける個数が少なければ、×を使った掛け算の形に直して計算すればよいのですが、99個も「−1」を書くのは非常に手間です。
そこで、もっと楽に計算できないかを考えてみましょう。
1は何個掛けても1ですから、考えなければいけないのは(−1)を99個掛けた後の符号が+か、−かです。
負の数の掛け算の符号ルールは次の通りです。
＜答えの符号の決め方（掛け算編）＞
1.同符号どうしの掛け算の答え→正の数（+）になる
例：−1×(−1)=1
2.異符号どうしの掛け算の答え→負の数（−）になる
例：−1×1=−1
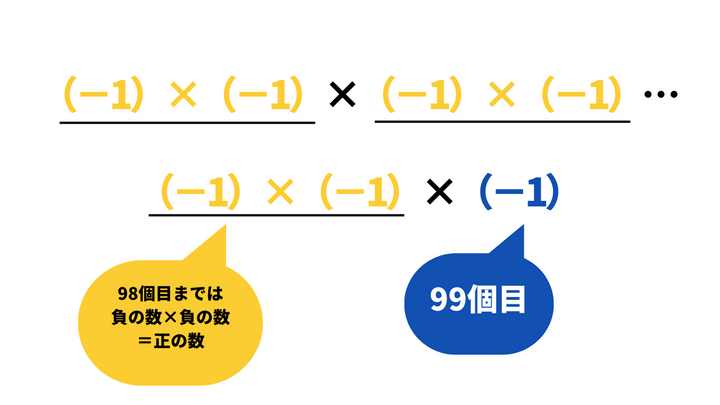
上記の同符号どうしの掛け算ルールから、掛け算の中に負の数二つのペアができれば答えは正だと分かります。(−1)を99個掛ける中で、98個目までは負の数が二つずつペアになる掛け算ですから、そこまでの掛け算の答えは正の数1です。
しかし、最後の99個目の掛け算では、1（=98個目までの掛け算の結果）×(−1)の計算が発生するので、答えは負の数になります。
よって、答えは負の数「−1」だと分かります。
まとめ
今回は、指数が大きい累乗を出題しました。
「−1」の累乗の場合は、指数が大きくても1を何個も掛けるだけですから、数字部分の計算は簡単です。また、答えの符号が+か−かは、負の数の計算ルールを応用すれば指数を見て判断できます。
なお、今回紹介した考え方は、次のようにルール化できます。
・負の数の累乗で指数が偶数の場合→答えは正の数（+）
・負の数の累乗で指数が奇数の場合→答えは負の数（−）
このルールを使えば、「−1」の累乗は、指数が偶数か奇数かを見るだけで、すぐに答えが出せますよ。
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。
文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。
もう一問挑戦！
