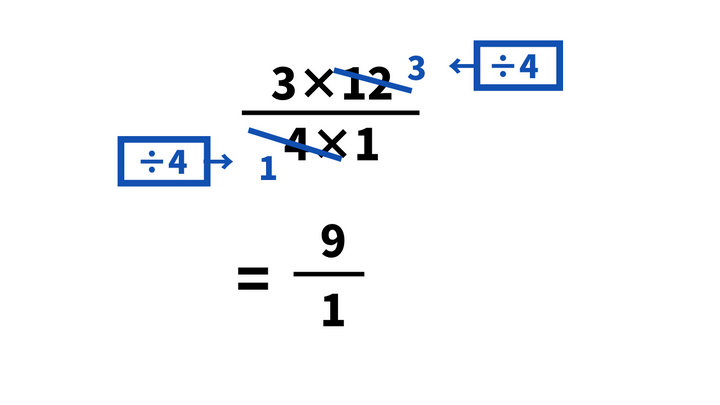小学生でも分かる問題に挑戦！「3/4×12」→正しく計算できる？

今回は、小学校で習う分数の問題に挑戦です。

小学生にとっては基礎レベルの問題かもしれませんが、分数の計算から離れてしまっている大人にとっては、難しく感じるかもしれません。

「あれ、どうやって計算するんだっけ？」と思ったなら、ぜひ解答だけでなく計算過程を解説した「ポイント」まで読んでみてください。

問題

次の計算をしなさい。
3/4×12

正解は、「9」です。

あなたが出した答えと一致したでしょうか。

久しぶりの分数の計算、どのように進めたらよいのか、戸惑った人もいるかもしれませんね。

次の「ポイント」で、分数の掛け算ルールを一緒に復習してみましょう。

今回の問題のポイントとなる分数の掛け算では、「分子どうし、分母どうしをそれぞれ掛けること」が基本ルールです。

<分数の掛け算のルール>

a/b×c/d=(a×c)/(b×d)

今回の問題は、分数×整数なので、一見このルールが使えないように見えます。しかし、整数は分母1の分数としても表せます。

掛ける数の12を12/1という分数形式に直せば、分数の掛け算のルールで計算ができますね。

3/4×12
=3/4×12/1
=(3×12)/(4×1)
=36/4

さて、分数の計算の答えは、「もうそれ以上約分できない分数」（既約分数）で表すのが一般的です。

約分とは、分子と分母を同じ数で割って、簡単な数で表すことです。36/4の場合は、分子と分母を同じ4で割れば約分ができますね。

36/4
=(36÷4)/(4÷4)
=9/1
=9

12を12/1にしたのとは反対に、9/1を9という整数にすれば、今回の問題の答えが出ます。

この問題をもっと効率的に計算したいなら、掛け算の前に約分するのがおすすめです。

この計算方法では、分子どうし、分母どうしを掛けるところまでは先の解説と同じですが、「3×12」を計算する前に一度ストップします。

3/4×12
=3/4×12/1
=(3×12)/(4×1)

分子の12と分母の4は共通の4で割れるため、掛け算をする前に約分をしてしまいましょう。

(3×12÷4)/(4÷4×1)
=(3×3)/(1×1)
=9/1

「3×12」を計算してから約分するよりも簡単に答えが出ますね。

このように分数の掛け算では、分子どうし、分母どうしの掛け算をする前に約分をした方が楽に計算できることが多くなります。

今回は、分数の計算問題に挑戦しました。

分数の掛け算に戸惑ってしまった人は、「分子どうし、分母どうしをそれぞれ掛ける」という計算ルールをぜひ覚えてください。また、約分の仕方も同時に身に付けておきましょう。分数の掛け算であれば、掛け算をする前に約分をした方が効率的ですよ。

小学校レベルの問題でも、久々に挑戦してみると、意外にルールを忘れていることがあります。このシリーズでは、小学校で習う懐かしい問題もたびたび取り上げていますので、引き続き挑戦してみてくださいね。

※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。

文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。

類似の数学問題にもう1問挑戦！

計算方法を覚えてる？「3/5+0.7」→正しく計算できる？