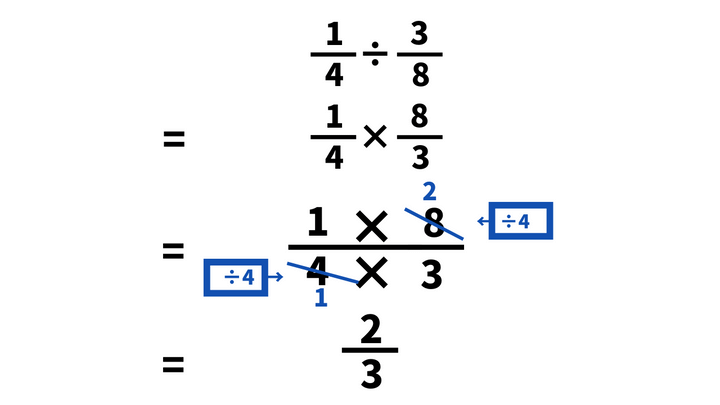50代でむくみがツラい人は絶対やって！【日本初】有名医師が監修したむくみ軽減法
PR(さくらフォレスト株式会社)
今回は、懐かしい算数の問題にチャレンジです。
分数の割り算は小学生のころに習ったはずですが、今でもスムーズに計算できるでしょうか？ 一度、試してみてください。
問題
次の計算をしなさい。
1/4÷3/8
解答
正解は、「2/3」です。
問題なく答えられたでしょうか？
どうやって計算すればよいのかすっかり忘れていたという人は、ぜひ次の「ポイント」をご覧ください。
分数の割り算の計算ルールを復習できますよ。
ポイント
分数の割り算のポイントは、「割る数の分子と分母を逆にして掛けること」です。
今回の問題でいえば、3/8の分子と分母を反対にした数、8/3を1/4に掛けます。
なお、分数の掛け算では、分子どうし・分母どうしを掛けます。
では、実際に計算してみましょう。
1/4÷3/8
=1/4×8/3
=(1×8)/(4×3)
ここで一つ注意点があります。分数の計算結果は、基本的にそれ以上約分できない形（既約分数）で求めなくてはなりません。
約分とは分子と分母を同じ数で割ることです。分数は、分子と分母を同じ数で割っても表している数は変わりません。よって約分すれば、同じ数をできるだけ簡単な分数で表せるのです。
なお、約分は掛け算の後よりも、掛け算の前にした方が楽になります。
今回も、掛け算の前に約分してしまいましょう。
(1×8)/(4×3) ←分子の8と分母の4を4で割って約分する
=(1×2)/(1×3)
=2/3
これで答えにたどり着きましたね。
まとめ
今回の問題で、分数の割り算の基本ルールを思い出せたでしょうか。
このルールは、「割る数の分子と分母を逆にして、割られる数に掛ける」というシンプルなものです。ただし、ただ掛け算をするだけではなく、約分ができるかどうかに注意しながら進めることが大事になります。
他にも、小学校で習った算数のルールを復習できる問題を用意していますので、引き続き挑戦してみてくださいね。
※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。あくまでも一例のご紹介に留まることを、ご了承ください。
文（編集）：VY
数学とIT技術学習が趣味のWebライター。実用数学技能検定2級と数学教員免許を取得後、家庭教師や学習支援スタッフとして数学指導を行ってきた。文系と理系の別、年齢にとらわれない、誰でも楽しめる数学解説作成を目指している。
もう一問挑戦！
