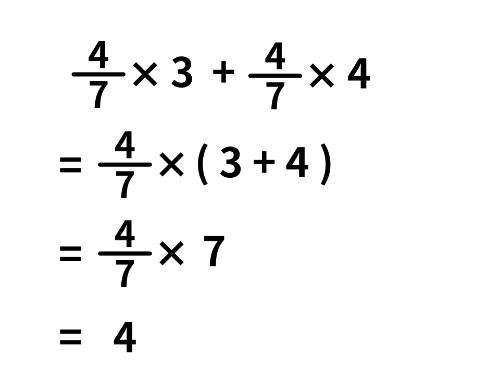どこから計算すればいい？「(4/7)×3+(4/7)×4」→正しく計算できる？

四則演算には計算の順序が決まっていますが、ちょっとした工夫で計算の順序を変えると、とても簡単に解けることがあります。

今回は、そんな問題に挑戦してみましょう。

問題

次の計算をしなさい。
(4/7)×3+(4/7)×4

掛け算と足し算、さらに分数の混じった計算です。

通常は掛け算から計算をしなければいけないのですが、分数もあるので少し手間のかかる計算になりそうです。

工夫をすることができないでしょうか。

解説

今回の問題の答えは「4」です。

途中の計算は次のようになります。

ここでは「分配法則」を用いて計算しています。

分配法則とは、次のような計算法則です。

＜分配法則＞
A×C−B×C =(A−B)×C

今回の問題は「(4/7)×3+(4/7)×4」と、「(4/7)×」の計算が二回出てきています。同じ掛け算を二回しているので、一回にまとめ、残った部分をカッコに入れます。

すると「(4/7)×(3+4)」となり、「(4/7)×」の計算が一回だけになりました。

分数の計算は、計算する回数が増えると、ミスをする可能性が高くなります。このようなときに、分配法則を利用することで、計算ミスの可能性を減らすことができます。

また、「掛け算を優先する」通常の計算順序で計算すると、次のようになります。

【別解】
  (4/7)×3+(4/7)×4
=(12/7)+(16/7)
=28/7
=4

同じ計算結果になりました。

もちろんこれでも間違いではないですが、分配法則を利用した方が簡単に答えを求めることができますね。

まとめ

「分配法則」は、計算の工夫でよく利用されます。

うまく活用することで、簡単に、そして正確に計算ができるようになるので、ぜひ使いこなせるようになりましょう！

※当メディアでご紹介する数学関連記事においては、複数の解法をもつものもございます。
あくまでも一例のご紹介に留まることを、ご了承ください。

---

---

文（編集）：SAJIMA
日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」

---

類似問題に挑戦！