問題設定
根付き木を考える。
この木のノード (頂点) は、親ノード (根には無い) と、値をもつ。
この木の中のノード1個を指定して、そのノードを根とするサブツリーに含まれるノードの値の合計を求める。
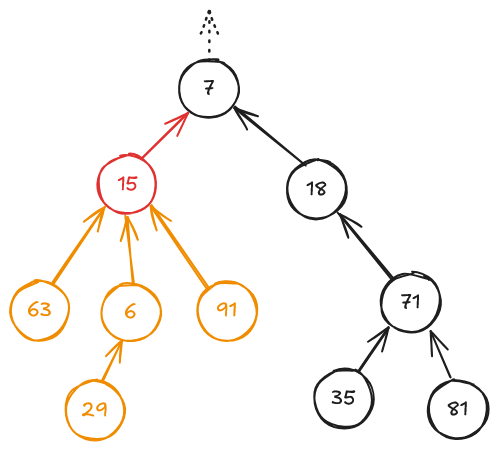
以下の図は、今回扱う木の例である。
丸がノードを、丸から出ている矢印が指す先のノードが親ノード、丸に書かれた数値が値である。
たとえば、赤いノード (値15) を指定したとき、そのノードを根とするサブツリーに含まれるノードは赤いノードとオレンジのノードであり、その値の合計は
実装
今回用意した問題を、SQLite で表現した。
また、SQLite の呼び出しには Python を用いた。
ノードを格納するテーブルの作成
ノードのID id、親ノードのID parent、値 value を格納するテーブルを作成する。
CREATE TABLE nodes(
id INTEGER NOT NULL PRIMARY KEY,
parent INTEGER,
value INTEGER NOT NULL
) STRICT
ノードの作成
まず、親ノードを持たない (すなわち、parent が NULL である) 根ノードを作成する。
db.execute(
"INSERT INTO nodes (id, value) VALUES (0, ?)",
(rng.randrange(1000), )
)
残りのノードを作成する。
作成するノードの親ノードは、これまでに作成したノードの中からランダムに選ぶ。
for i in range(1, node_num):
db.execute(
"INSERT INTO nodes (id, parent, value) VALUES (?, ?, ?)",
(i, rng.randrange(i), rng.randrange(1000))
)
クエリの実行
再帰SQLを用いて指定したノードを根とするサブツリーに含まれるノードを列挙し、それらの値の合計を求める。
ノードの列挙は、以下の手順で行う。
- 根となるノードを結果に加える
- 前回のステップで結果に加えたノードのいずれかを親とするノードを結果に加える
- 結果に加えるノードが無くなるまで、2 を繰り返す
WITH RECURSIVE decendents (id, value) AS (
SELECT id, value FROM nodes WHERE id = ?
UNION ALL
SELECT nodes.id, nodes.value
FROM nodes
INNER JOIN decendents ON decendents.id = nodes.parent
)
SELECT SUM(value) FROM decendents
再帰SQLについて詳しくは、以下のページなどが参考になる。
インデックスの作成
今回は指定のノードを親ノードとするノードを検索したいので、親ノードを表す列 parent に対してインデックスを作成する。
CREATE INDEX parent_index ON nodes (parent)
コード全体
乱数系列を固定し、同じパラメータであれば処理内容が同じになるようにした。
time.perf_counter() を用いてノードの作成およびクエリの実行にかかった時間を計測した。
(参考:[Python][Tips] 処理時間の計測 #Python3 - Qiita)
import random
import sqlite3
import sys
import time
def test(use_index, node_num, query_num):
rng = random.Random(3141592)
db = sqlite3.connect(":memory:")
db.execute("""
CREATE TABLE nodes(
id INTEGER NOT NULL PRIMARY KEY,
parent INTEGER,
value INTEGER NOT NULL
) STRICT
""")
if use_index:
print("using index")
db.execute("CREATE INDEX parent_index ON nodes (parent)")
else:
print("not using index")
start_time = time.perf_counter()
db.execute(
"INSERT INTO nodes (id, value) VALUES (0, ?)",
(rng.randrange(1000), )
)
for i in range(1, node_num):
db.execute(
"INSERT INTO nodes (id, parent, value) VALUES (?, ?, ?)",
(i, rng.randrange(i), rng.randrange(1000))
)
insert_end_time = time.perf_counter()
all_sum = 0
for _ in range(query_num):
res = db.execute(
"""
WITH RECURSIVE decendents (id, value) AS (
SELECT id, value FROM nodes WHERE id = ?
UNION ALL
SELECT nodes.id, nodes.value
FROM nodes
INNER JOIN decendents ON decendents.id = nodes.parent
)
SELECT SUM(value) FROM decendents
""",
(rng.randrange(node_num), )
)
res_row = res.fetchone()
all_sum += res_row[0]
query_end_time = time.perf_counter()
print("sum = " + str(all_sum))
print("insert time = " + str(insert_end_time - start_time) + " sec.")
print("query time = " + str(query_end_time - insert_end_time) + " sec.")
print("total time = " + str(query_end_time - start_time) + " sec.")
node_num = int(sys.argv[1]) if len(sys.argv) > 1 else 10000
query_num = int(sys.argv[2]) if len(sys.argv) > 2 else node_num
test(True, node_num, query_num)
test(False, node_num, query_num)
実行結果
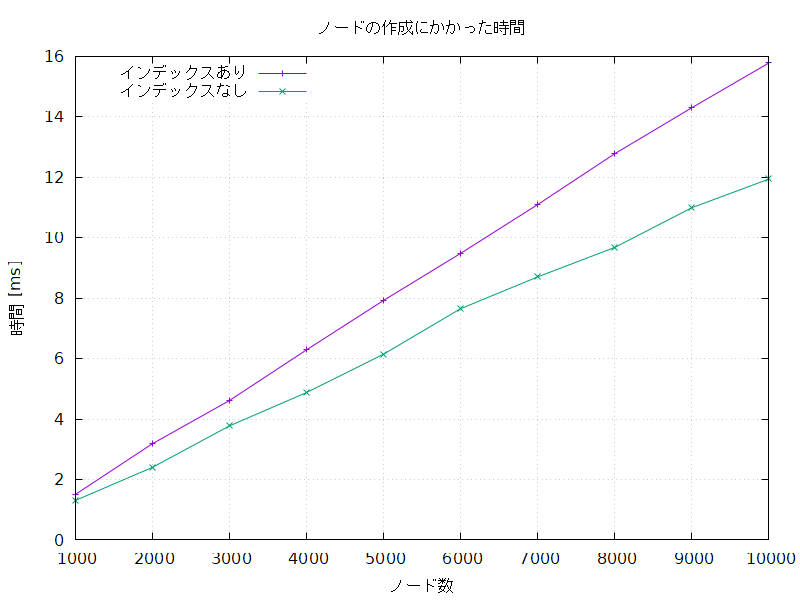
クエリを実行する回数はノードの数によらず 10,000 回で固定し、作成するノードの数を変えて実行した。
以下に、それぞれの処理にかかった時間 [ms] を示す。
測定はそれぞれ5回行い、平均をとった。
| ノード数 | インデックスあり ノード作成 |
インデックスあり クエリ実行 |
インデックスなし ノード作成 |
インデックスなし クエリ実行 |
|---|---|---|---|---|
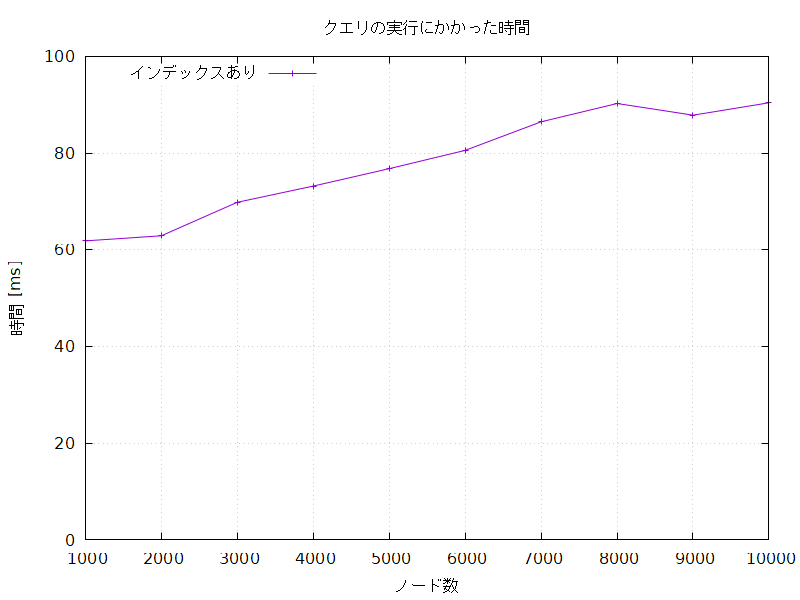
| 1000 | 1.500 | 61.847 | 1.302 | 2250.769 |
| 2000 | 3.179 | 62.895 | 2.397 | 5097.825 |
| 3000 | 4.610 | 69.825 | 3.771 | 8241.450 |
| 4000 | 6.286 | 73.178 | 4.875 | 11370.362 |
| 5000 | 7.923 | 76.783 | 6.146 | 14641.931 |
| 6000 | 9.481 | 80.560 | 7.651 | 17587.348 |
| 7000 | 11.966 | 86.474 | 8.704 | 20948.993 |
| 8000 | 12.780 | 90.250 | 9.680 | 24705.844 |
| 9000 | 14.302 | 87.841 | 10.993 | 27794.540 |
| 10000 | 15.784 | 90.407 | 11.942 | 30919.401 |
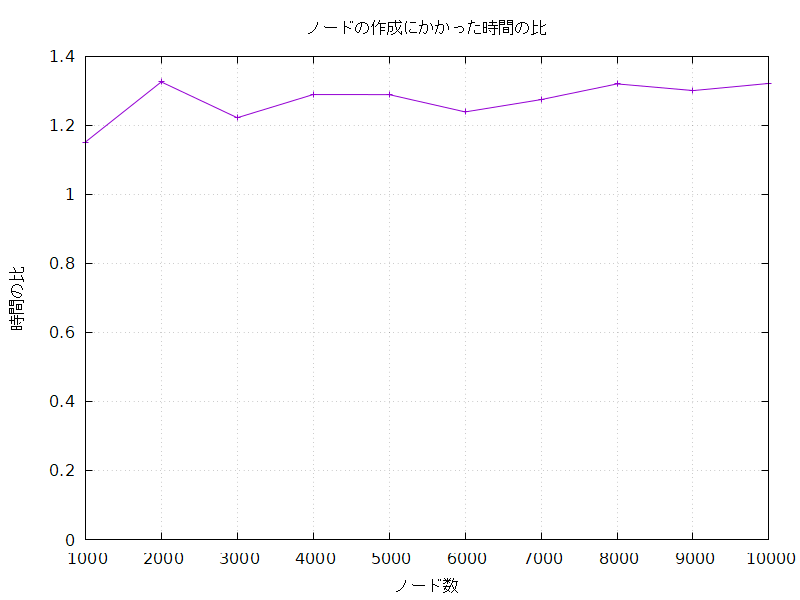
ノードの作成にかかった時間の比較
ノード数にかかわらず、インデックスありでの処理のほうがインデックスなしでの処理よりも長時間かかった。
インデックスありでの処理時間をインデックスなしでの処理時間で割った比を求めてみると、どのノード数でもだいたいインデックスありでの処理にはインデックスなしでの処理の約1.3倍の時間がかかっていることがわかった。
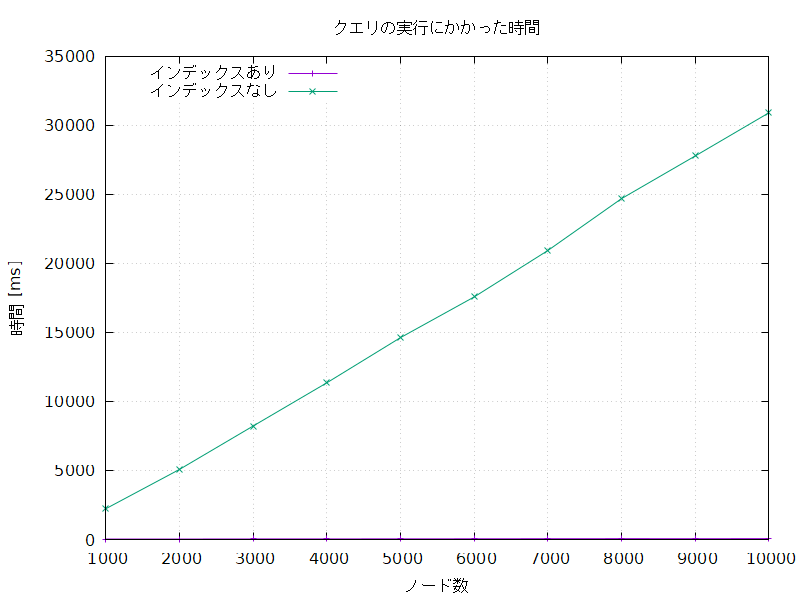
クエリの実行にかかった時間の比較
インデックスなしの処理はインデックスありの処理に比べて圧倒的に長時間かかり、かかる時間はノード数が増えるにつれてどんどん長くなっていった。
インデックスありの処理にかかる時間もノード数が増えるにつれて長くなる傾向にあるが、その増え方はインデックスなしの処理に比べて穏やかである。
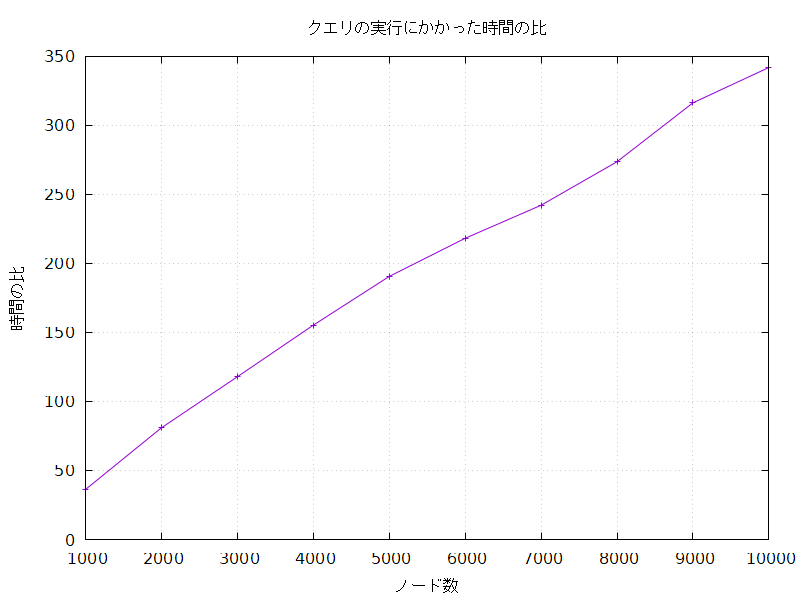
インデックスなしでの処理時間をインデックスありでの処理時間で割った比 (長い方を割られる数にするため、ノードの作成にかかった時間の比とは逆である) を求めてみると、これもまたノード数が増えるにつれてどんどん大きくなっていった。
結論
今回の問題設定と実装では、インデックスを作ったときは、作っていないときに比べてノードの作成のコストは約1.3倍と大きくなるが、そのかわりクエリの実行のコストは数十~数百分の1と大幅に小さくなることがわかった。
ノードの作成や更新の回数に比べて参照の回数が十分多い場合は、参照時に「この列が特定の値である行が欲しい」となる列のインデックスを作っておくことで、処理の効率を上げる効果が期待できる。
おまけ
「SQLite インデックス」でググったら出てきた先行研究。より単純な例を扱っている。
DBにインデックスを貼るとどれくらい速くなるのか #SQL - Qiita
蛇足
インデックスがCV:井口裕香だという噂があったかもしれない…?
井口裕香といえば、柳冨美子役、園田優役、ミミ・ウリエ・フォン・シュヴァルツラング役などがあるよね…。
Comments
Let's comment your feelings that are more than good