maisvendoo 30 июн 2015 в 10:48

Магия тензорной алгебры: Часть 1 — что такое тензор и для чего он нужен?

7 мин

363K

Содержание

Введение

Это было очень давно, когда я учился классе в десятом. Среди довольно скудного в научном плане фонда районной библиотеки мне попалась книга — Угаров В. А. «Специальная теория относительности». Эта тема интересовала меня в то время, но информации школьных учебников и справочников было явно недостаточно.

Однако, книгу эту я читать не смог, по той причине, что большинство уравнений представлялись там в виде тензорных соотношений. Позже, в университете, программа подготовки по моей специальности не предусматривала изучение тензорного исчисления, хотя малопонятный термин «тензор» всплывал довольно часто в некоторых специальных курсах. Например, было жутко непонятно, почему матрица, содержащая моменты инерции твердого тела гордо именуется тензором инерции.

Погружение в специальную литературу не приносило просветления. Технарю достаточно тяжело переварить строгий абстрактный язык чистой математики. Тем не менее, от случая к случаю я возвращался к этому вопросу, и вот спустя почти шестнадцать лет наступило просветление, о чем и будет рассказано под катом. Возможно, мои рассуждения покажутся примитивными и упрощенными, но понимание любой сложной вещи принято разворачивать от процесса оперирования простыми понятиями, поэтому начнем.

1. Вектор на плоскости. Контравариантные, ковариантные координаты и связь между ними

Рассмотрим вектор, и без потери общности наших рассуждений, рассмотрим вектор заданный на плоскости. Как известно из курса ещё школьной геометрии, любой вектор можно задать на плоскости с помощью двух неколлинеарных векторов

$\vec{a} = a^1 \vec{e}_1 + a^2 \vec{e}_2.\quad (1)$

Здесь $a^i,\, i = \overline{1,2}$ — коэффициенты разложения, (под верхним индексом следует понимать именно номер компоненты, а не возвдение в степень), называемые контрвариантные координаты вектора $\vec{a}$ . Геометрически это можно изобразить так, как показано на рисунке ниже. Векторы $\vec{e}_1, \vec{e}_2$ называют базисными, угол между ними, при условии $\varphi \ne 0,\pi$ , может быть произвольным, произвольна так же ненулевая длина базисных векторов. Указанный базис задает косоугольную систему координат на плоскости, с осями (u,v) .

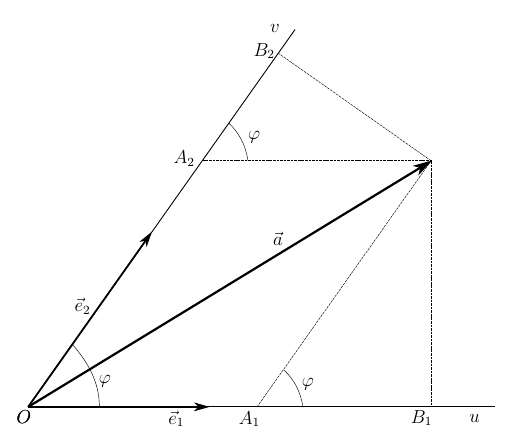
Рис.1. Вектор в косоугольных координатах на плоскости

Исходя из чертежа длины отрезков OA_1 и OA_2 равны

$OA_1 = a^1 \left|\vec{e}_1 \right|,\, OA_2 = a^2 \left|\vec{e}_2 \right|\quad (2)$

Однако, это не единственный способ определить вектор $\vec{a}$ в данной системе координат. Его можно так же задать ортогональными проекциями на оси (u, v) . Нетрудно видеть, что эти проекции равны

$&OB_1 = OA_1 + OA_2\cos\varphi = a^1 \left|\vec{e}_1 \right| + a^2 \left|\vec{e}_2 \right| \cos\varphi\quad (3) \\ &OB_2 = OA_1\cos\varphi + OA_2 = a^1 \left|\vec{e}_1 \right|\cos\varphi + a^2 \left|\vec{e}_2 \right|\quad (4)$

С другой стороны, выразим длины этих проекций через длины базисных векторов таким образом
$&OB_1 = a_u = \frac{\vec{a} \cdot \vec{e}_1}{\left|\vec{e}_1 \right|} = \frac{a_1}{\left|\vec{e}_1 \right|} \quad (5) \\ &OB_2 = a_v = \frac{\vec{a} \cdot \vec{e}_2}{\left|\vec{e}_2 \right|} = \frac{a_2}{\left|\vec{e}_2 \right|}\quad (6)$

где $a_1 = \vec{a} \cdot \vec{e}_1$ и $a_2 = \vec{a} \cdot \vec{e}_2$ — ковариантные координаты вектора $\vec{a}$ .

Сравниваем (3), (5) и (4), (6)

$&\frac{a_1}{ \left|\vec{e}_1 \right|} = a^1 \left|\vec{e}_1 \right| + a^2 \left|\vec{e}_2 \right| \cos\varphi \quad (7) \\ &\frac{a_2}{ \left|\vec{e}_2 \right|} = a^1 \left|\vec{e}_1 \right|\cos\varphi + a^2 \left|\vec{e}_2 \right| \quad (8)$

Умножим (7) на $\left|\vec{e}_1 \right|$ , а (8)
на $\left|\vec{e}_2 \right|$ и преобразуем их

$&a_1 = a^1(\vec{e}_1 \cdot \vec{e}_1) + a^2 (\vec{e}_1 \cdot \vec{e}_2) \quad (9) \\ &a_2 = a^1(\vec{e}_1 \cdot \vec{e}_2) + a^2 (\vec{e}_2 \cdot \vec{e}_2) \quad (10)$

Введем матрицу

$\mathbf{g} = \begin{bmatrix} \vec{e}_1 \cdot \vec{e}_1 && \vec{e}_1 \cdot \vec{e}_2 \\ \vec{e}_1 \cdot \vec{e}_2 && \vec{e}_2 \cdot \vec{e}_2 \end{bmatrix} \quad (11)$

тогда (9) и (10) можно выразить следующим соотношением

$a_i = \sum_{j=1}^{2} g_{ij} a^j,\, i=1,2 \quad (12)$

Выражение (12) дает связь между ковариантными и контрaвариантными координатами вектора, определяемую лишь видом матрицы $\mathbf{g}$ , зависящей от длин взаимного расположения базисных векторов. Пока никак не будем интерпретировать полученный результат, а просто запомним его.

Набор контравариантных и ковариантных компонент, по сути, задают в выбранном базисе один и тот же вектор. При использовании контравариантных координат этот вектор задается матрицей-столбцом

$\mathbf{a} = \begin{bmatrix} a^1 \\ \vdots \\ a^n \end{bmatrix}$

а в ковариантной форме — матрицей-строкой

$\mathbf{a} = \begin{bmatrix} a_1 && \cdots && a_n \end{bmatrix}$

2. Скалярное произведение векторов

Перейдем к пространству более высокой размерности и рассмотрим два вектора

$\label{eq:3d-vectors} \vec{a} = a^1 \vec{e}_1 + a^2 \vec{e}_2 + a^3 \vec{e}_3,\, \vec{b} = b^1 \vec{e}_1 + b^2 \vec{e}_2 + b^3 \vec{e}_3$

где базисные векторы $\vec{e}_1,\vec{e}_2, \vec{e}_3$ , как и выше, ненулевые
некомпланарные векторы. Перемножим векторы $\vec{a}$ и $\vec{b}$ скалярно.

$\vec{a} \cdot \vec{b} = \left(a^1 \vec{e}_1 + a^2 \vec{e}_2 + a^3 \vec{e}_3\right) \cdot \left(b^1 \vec{e}_1 + b^2 \vec{e}_2 + b^3 \vec{e}_3\right)$

В последнем выражении аккуратно раскроем скобки

$\vec{a} \cdot \vec{b} = &a^1 b^1 (\vec{e}_1 \cdot \vec{e}_1 ) + a^2 b^1 (\vec{e}_1 \cdot \vec{e}_2 ) + a^3 b^1 (\vec{e}_1 \cdot \vec{e}_3 ) + \\ &a^1 b^2 (\vec{e}_1 \cdot \vec{e}_2 ) + a^2 b^2 (\vec{e}_2 \cdot \vec{e}_2 ) + a^3 b^2 (\vec{e}_2 \cdot \vec{e}_3 ) + \\ &a^1 b^3 (\vec{e}_1 \cdot \vec{e}_3 ) + a^2 b^3 (\vec{e}_2 \cdot \vec{e}_3 ) + a^3 b^3 (\vec{e}_3 \cdot \vec{e}_3 )$

и снова введем матрицу

$\mathbf{g} = \begin{bmatrix} \vec{e}_1 \cdot \vec{e}_1 && \vec{e}_1 \cdot \vec{e}_2 && \vec{e}_1 \cdot \vec{e}_3 \\ \vec{e}_1 \cdot \vec{e}_2 && \vec{e}_2 \cdot \vec{e}_2 && \vec{e}_2 \cdot \vec{e}_3 \\ \vec{e}_1 \cdot \vec{e}_3 && \vec{e}_2 \cdot \vec{e}_3 && \vec{e}_3 \cdot \vec{e}_3 \end{bmatrix} \quad (14)$

и тогда скалярное произведение можно свернуть весьма компактным образом

$\vec{a} \cdot \vec{b} = \sum_{i=1}^3 \left(\sum_{j=1}^3 g_{ij} a^j\right) b^i \quad (15)$

Первое, что можно заметить, при уменьшении числа измерений пространства мы перейдем от (14) к (11) а выражение
(15) будет работать и давать склярное произведение векторов, но уже на плоскости. То есть мы получили некую обобщающую форму записи операции скалярного умножения, не зависящую ни от размерности пространства, ни от рассматриваемого базиса, все свойства которого обраны в матрице $\mathbf{g}$ . Внимательно взглянув на (15) мы поймем ещё одну вещь

$a_i = \sum_{j=1}^3 g_{ij} a^j,\, i=1,2,3 \quad (16)$

что есть ничто иное как ковариантные координаты вектора $\vec{a}$ . То есть, (15) можно переписать

$\vec{a} \cdot \vec{b} = \sum_{i=1}^3 a_i b^i \quad (17)$

Но и это не предел упрощения

3. Правило Эйнштейна

Хитный и проницательный Альберт Эйнштейн придумал правило суммирования, в выражениях подобных (17), избавляющее математика от надоедливой и избыточной $\sum$ . В выражениях (16) и (17) можно опустить знак суммы, подразумевая суммирование по повторяющемуся индексу, который называют «немым». То есть, (16) переписываем так

$a_i = g_{ij}\, a^j,\, i=1,2,3 \quad (18)$

здесь j — индекс, по которому происходит суммирование. По правилу, этот индекс должен чередовать свое положение — если у первого множителя он внизу, то у второго должен быть вверху и наоборот. Выражение (17) будет выглядеть так

$\vec{a} \cdot \vec{b} = a_i\, b^i \quad (19)$

Ну а (15) придет к виду

$\vec{a} \cdot \vec{b} = g_{ij}\, a^j\, b^i \quad (20)$

А теперь мы посмотрим, для чего надо было городить такой огород.

4. Анализ на простых примерах

Допустим, что наш базис — декартов, то есть ортонормированый. Тогда, матрица $\mathbf{g}$ становится единичной

$\mathbf{g} = \begin{bmatrix} 1 && 0 && 0 \\ 0 && 1 && 0 \\ 0 && 0 && 1 \end{bmatrix}$

Пусть вектор $\vec{a}$ задан в таком базисе. Квадрат длины вектора, как известно, это скалярное произведение этого вектора самого на себя, то есть

$|\vec{a}|^2 = \vec{a} \cdot \vec{a} = g_{ij}\, a^j\, a^i = &\left(g_{11} a^1 + g_{12} a^2 + g_{13} a^3\right) a^1 + \\ & + \left(g_{21} a^1 + g_{22} a^2 + g_{23} a^3\right) a^2 + \\ & + \left(g_{31} a^1 + g_{32} a^2 + g_{33} a^3\right) a^3 = \\ & = (a^1)^2 + (a^2)^2 + (a^3)^2$

И мы получили… квадрат длины вектора, заданного в прямоугольной системе координат!

Ещё пример, дабы не загроможнать который, будем работать в двух измерениях. Пусть система координат подобна той, что изображена на рисунке из параграфа 1, и в ней задан вектор $\vec{b}$ своими контравариантными rоординатами. Тогда

$\mathbf{g} = \begin{bmatrix} 1 && \cos\varphi \\ \cos\varphi && 1 \end{bmatrix}$

где $\varphi$ — угол между векторами базиса. Вычислим длину вектора $\vec{b}$

$|\vec{b}|^2 = \vec{b} \cdot \vec{b} = g_{ij}\, b^j\, b^i = &\left(g_{11} b^1 + g_{12} b^2\right) b^1 + \left(g_{21} b^1 + g_{22} b^2\right) b^2 = \\ & = (b^1)^2 + b^2\, b^1 \cos\varphi + b^1\, b^2 \cos\varphi + (b^2)^2 = \\ & = (b^1)^2 + (b^2)^2 + 2\, b^1\, b^2 \cos\varphi$

Ровно такой же результат мы получим, если воспользуемся теоремой косинусов и найдем квадрат длины диагонали параллелограмма.

Что получается? Работая в разных системах координат, мы использовали одну единственную формулу (20) для вычисления скалярного произведения. И её вид совершенно не зависит ни от базиса, ни от числе измерений пространства, в котором мы работаем. Базисом определяются лишь конкретные значения компонент матрицы $\mathbf{g}$ .

Так вот, уравнение (20) выражает скалярное произведение двух векторов в тензорной, то есть независимой от выбранного базиса форме.

Матрица $\mathbf{g}$ задает так называемый метрический тензор. Её вид
определяет каким образом в выбранных координатах вычисляется расстояние между двумя точками.

Но почему мы называем эту матрицу тензором? Следует понимать, что математическая форма, в данном случае квадратная матрица, содержащая набор компонент, это ещё не тензор. Понятие тензора несколько шире, и прежде чем мы скажем, что такое тензор, мы рассмотрим ещё один вопрос.

5. Преобразование метрического тензора при смене базиса

Перепишем соотношение (20) в матричной форме, так нам будет легче оперировать им

$c = \mathbf{a}^{(0)T}\, \mathbf{g}^{(0)}\, \mathbf{b}^{(0)} \quad (21)$

где c — скалярное произведение векторов. Верхний индекс несет смысл системы координат, в которой заданы векторы и определен метрический тензор. Скажем это система координат СК0. Преобразование вектора к некоторой другой системе
координат СК1 описывается матрицей преобразования $\mathbf{A}_{01}$ , то есть

$\mathbf{a}^{(0)} = \mathbf{A}_{01}\, \mathbf{a}^{(1)}, \quad \mathbf{b}^{(0)} = \mathbf{A}_{01}\, \mathbf{b}^{(1)} \quad (22)$

Подставим (22) в (21)
$c = \left(\mathbf{A}_{01}\, \mathbf{a}^{(1)}\right)^T\, \mathbf{g}^{(0)}\,\mathbf{A}_{01}\, \mathbf{b}^{(1)} = \mathbf{a}^{(1)T}\, \mathbf{A}_{01}^T \mathbf{g}^{(0)}\,\mathbf{A}_{01}\, \mathbf{b}^{(1)}$

в последнем выражении

$\mathbf{A}_{01}^T \mathbf{g}^{(0)}\,\mathbf{A}_{01} = \mathbf{g}^{(1)}$

метрический тензор, компоненты которого определяются новым базисом. То есть, в новом базисе операция имеет аналогичную форму

$c = \mathbf{a}^{(1)T}\, \mathbf{g}^{(1)}\, \mathbf{b}^{(1)}$

Тем самым мы показали ещё одно свойство тензора — его компоненты меняются синхронно с компонентами векторов того пространства, в котором определен тензор. То есть теперь мы можем сказать, что тензор — это математический объект, представленный набором компонент и правилом их преобразования при смене базиса.

Теперь, используя правило Эйнштейна, перепишем (22) и (23) в тензорной форме

$a^{i(1)} = \alpha_k^i a^{k(0)}, \quad b^{i(1)} = \alpha_k^i b^{k(0)} \quad (24)$

$g_{ij}^{(1)} = \alpha_i^l \, \alpha_j^k \, g_{kl}^{(0)} \quad (25)$

где $\alpha_p^q$ — элементы матрицы $\mathbf{A}_{01}$ . Проиллюстрируем (25) на трехмерном примере. Пусть матрица преобразования координат имеет вид

$\mathbf{A}_{01} = \begin{bmatrix} \alpha_1^1 &&\alpha_2^1 && \alpha_3^1 \\ \alpha_1^2 &&\alpha_2^2 && \alpha_3^2 \\ \alpha_1^3 &&\alpha_2^3 && \alpha_3^3 \end{bmatrix}$

Распишем преобразование компонента метрического тензора, выполняя суммирование по немым индексам k и l в (25)

$g_{ij}^{(1)} = & \alpha_i^1 \, \left( \alpha_j^1 \, g_{11}^{(0)} + \alpha_j^2 \, g_{21}^{(0)} + \alpha_j^3 \, g_{31}^{(0)} \right) + \\ & \alpha_i^2 \, \left( \alpha_j^1 \, g_{12}^{(0)} + \alpha_j^2 \, g_{22}^{(0)} + \alpha_j^3 \, g_{32}^{(0)} \right) + \\ & \alpha_i^3 \, \left( \alpha_j^1 \, g_{13}^{(0)} + \alpha_j^2 \, g_{23}^{(0)} + \alpha_j^3 \, g_{33}^{(0)} \right)$

откуда видно что в (25) выполняется транспонирование матрицы перехода, умножение результата на метрический тензор и
умножение полученной матрицы на матрицу перехода.

Теперь рассмотрим конкретный пример, на плоскости, чтобы не писать излишне громоздких выкладок

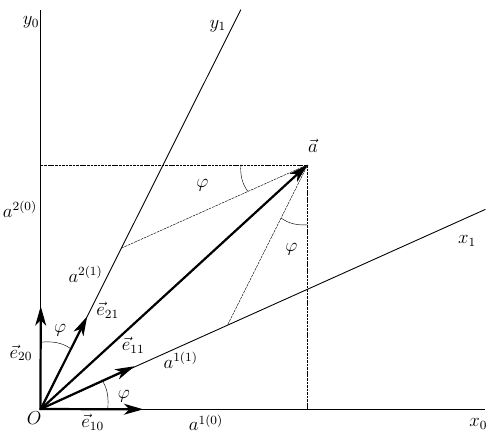
Пусть вектор $\vec{a}$ задан в двух нормированных базисах: прямоугольном
$(\vec{e}_{10}, \, \vec{e}_{20})$ и косоугольном $(\vec{e}_{11}, \, \vec{e}_{21})$ . Преобразование из косоугольной системы координат в прямоугольную выражается матрицей

$\mathbf{A}_{01} = \begin{bmatrix} \cos\varphi && \sin\varphi \\ \sin\varphi && \cos\varphi \end{bmatrix}$

обратное преобразование

$\mathbf{A}_{10} = \mathbf{A}_{01}^{-1} = \begin{bmatrix} \cfrac{\cos\varphi}{\cos 2 \varphi} && -\cfrac{\sin\varphi}{\cos 2 \varphi} \\ -\cfrac{\sin\varphi}{\cos 2 \varphi} && \cfrac{\cos\varphi}{\cos 2 \varphi} \end{bmatrix}$

Пусть также, в прямоугольных координатах наш вектор имеет компоненты

$\mathbf{a}^{(0)} = \begin{bmatrix} 3 \\ 4 \end{bmatrix}$

и совсем нетрудно увидеть, что длина его $|\vec{a}| = 5$ . Метрический тензор в ортонормированном базисе представляется единичной матрицей

$\mathbf{g}^{(0)} = \begin{bmatrix} 1 && 0 \\ 0 && 1 \end{bmatrix}$

значит

$|\vec{a}|^2 = g_{ij}^{(0)} \, a^{j(0)} \, a^{i(0)} & = \left( g_{11}^{(0)} \, a^{1(0)} + g_{12}^{(0)} \, a^{2(0)} \right) a^{1(0)} + \left( g_{21}^{(0)} \, a^{1(0)} + g_{22}^{(0)} \, a^{2(0)} \right) a^{2(0)} \\ & = 3 \cdot 3 + 4 \cdot 4 = 9 + 16 = 25.$

Зададим угол наклона осей $\varphi = \frac{\pi}{6}$ и вычислим контравариантные компоненты вектора в косоугольных осях

$&a^{1(1)} = \tilde{\alpha}_1^1 \, a^{1(0)} + \tilde{\alpha}_2^1 \, a^{2(0)} = 3\sqrt{3} - 4 \\ &a^{2(1)} = \tilde{\alpha}_1^2 \, a^{1(0)} + \tilde{\alpha}_2^2 \, a^{2(0)} = -3 + 4\sqrt{3}$

Вместе с вектором необходимо преобразовать и метрический тензор

$&g_{11}^{(1)} = \alpha_1^1 \, \left( \alpha_1^1 \, g_{11}^{(0)} + \alpha_1^2 \, g_{21}^{(0)} \right) + \alpha_1^2 \, \left( \alpha_1^1 \, g_{12}^{(0)} + \alpha_1^2 \, g_{22}^{(0)} \right) = \frac{\sqrt 3}{2} \cdot \frac{\sqrt 3}{2} + \frac{1}{2} \cdot \frac{1}{2} = 1 \\ &g_{12}^{(1)} = \alpha_1^1 \, \left( \alpha_2^1 \, g_{11}^{(0)} + \alpha_2^2 \, g_{21}^{(0)} \right) + \alpha_1^2 \, \left( \alpha_2^1 \, g_{12}^{(0)} + \alpha_2^2 \, g_{22}^{(0)} \right) =\frac{\sqrt 3}{2} \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{\sqrt 3}{2} = \frac{\sqrt 3}{2} \\ &g_{21}^{(1)} = \alpha_2^1 \, \left( \alpha_1^1 \, g_{11}^{(0)} + \alpha_1^2 \, g_{21}^{(0)} \right) + \alpha_2^2 \, \left( \alpha_1^1 \, g_{12}^{(0)} + \alpha_1^2 \, g_{22}^{(0)} \right) = \frac{1}{2} \cdot \frac{\sqrt 3}{2} + \frac{\sqrt 3}{2} \cdot \frac{1}{2} = \frac{\sqrt 3}{2} \\ &g_{22}^{(1)} = \alpha_2^1 \, \left( \alpha_2^1 \, g_{11}^{(0)} + \alpha_2^2 \, g_{21}^{(0)} \right) + \alpha_2^2 \, \left( \alpha_2^1 \, g_{12}^{(0)} + \alpha_2^2 \, g_{22}^{(0)} \right) = \frac{1}{2} \cdot \frac{1}{2} + \frac{\sqrt 3}{2} \cdot \frac{\sqrt 3}{2} = 1$

Ну а теперь вычислим длину вектора в новом базисе

$|\vec{a}|^2 = g_{ij}^{(1)} \, a^{j(1)} \, a^{i(1)} & = \left( g_{11}^{(1)} \, a^{1(1)} + g_{12}^{(1)} \, a^{2(1)} \right) a^{1(1)} + \left( g_{21}^{(1)} \, a^{1(1)} + g_{22}^{(1)} \, a^{2(1)} \right) a^{2(1)} = \\ & = \left( 3\sqrt 3 - 4 - 3\frac{\sqrt 3}{2} + 6 \right) \left(3\sqrt 3 - 4 \right) + \\ & + \left( \frac{9}{2} - 2\sqrt 3 - 3 + 4\sqrt 3 \right) \left(-3 + 4\sqrt 3\right) = \\ & = \frac{27}{2} + 6\sqrt 3 - 6\sqrt 3 - 8 - \frac{9}{2} - 6\sqrt 3 + 6\sqrt 3 + 24 = 9 + 16 = 25$

то есть

$|\vec{a}| = 5,$

и скалярное произведение и длина вектора инвариантны, то есть неизменны при преобразовании координат, а так и должно быть. При этом, мы использовали по сути одно и то же соотношение (20) для работы в разных базисах, предварительно преобразовав метрический тензор в соответствии с правилом преобразования векторов в рассматриваемых пространствах
(25).

Заключение и выводы

Что мы увидели в предыдущем параграфе? Если свойства пространства, в котором заданы векторы известны, то для нас не составляет труда выполнить, строго формальным образом, действия над векторами, используя соотношения, вид которых от формы пространства независим. Причем соотношения (20), (24) и (25) дают нам и алгоритм вычисления и способ преобразования компонент выражений, используемых алгоритмом. В этом — мощь и сила тензорного подхода.

Многие физические теории, например ОТО, оперируют искривленным пространством-временем, и там другой подход просто неприемлем. В искривленном пространстве-времени метрический тензор задан локально, в каждой его точке, и если попытаться обойтись без тензоров, у нас ничего не выйдет — мы получим громоздкие и неповоротливые уравнения, если получим их вообще.

В прикладных областях науки тензорная запись выражений применима там, где требуется получать уравнения, независимые от используемой системы координат.

Но это ещё не всё. Мы не поговорили о свойствах метрического тензора, не рассмотрели векторное произведение и тензор Леви-Чевиты. Не поговорили о ранге тензоров и операциях с ними, не разобрались до конца с правилами индексации компонент тензоров и о многом другом. Об этом будет написано несколько позднее, а пока — спасибо всем моим читателям за внимание.

Продолжение следует...

Теги:

Хабы:

Математика

+56

+89

Редакторский дайджест

Присылаем лучшие статьи раз в месяц

Дмитрий Притыкин @maisvendoo

Пользователь

Сайт Сайт Сайт

Комментарии 89

netmaxed 30 июн 2015 в 12:23

о да!
давно пора было освежить знания о тензорах!
ждем продолжения :)
P.S. очень хорошо и понятно пишете! спасибо.

НЛО прилетело и опубликовало эту надпись здесь

potan 30 июн 2015 в 13:38

Знакомство с тензорным исчислением и праволом Эйнштейна мне помогло и в программировании — в подходе к работе с коллекциями.

DrReiz 30 июн 2015 в 14:29

Интересно! Где — тензоры, а где — коллекции… Расскажи, пожалуйста, подробнее: как правило Эйнштейна помогло при работе с коллекциями?

potan 30 июн 2015 в 16:37

Такие операции с коллекциями как map, zip, fold (он же reduce) напоминают тензорные операции. Особенно это заметно на примере языков APL, R, Julia, но и в более мейнстримовых эта аналогия мне помогала.

kirilloid 30 июн 2015 в 19:30

Да, знание тензоров может помочь, но если тензоров не знаешь, то, конечно, пытаться через них понять zip/fold — совершенно бесполезная затея.

andy_p 30 июн 2015 в 15:32

Тогда вам надо с линейной алгебры рассказ начинать.

futureader 30 июн 2015 в 18:55

Вообще, было бы не плохо начать с того, а зачем это все надо. А надо это для того, что бы описывать объекты в пространстве без учета системы координат. Так, когда описывают вектор как тензор, то имеют ввиду именно вектор как объект (буквально — палочку со стрелочкой), а не связанные с ним координаты в той или иной системе координат. Таким образом, когда мы начинаем смотреть на этот вектор из разных систем, то вектор (палочка со стрелочкой) не меняется, а меняется лишь его представление в системе координат. Поэтому, вектор силы, например — это тензор.

НЛО прилетело и опубликовало эту надпись здесь

futureader 30 июн 2015 в 19:32

Как-то не очень понятно, что Вы имеете ввиду. Честно говоря, можно что угодно называть тензором, только тензором в математическом плане оно от этого является не будет. Для задания тензоров нужно — линейное пространство (ваши катушки?) и простарнство линейных форм (что это в вашем случае?) Аналогию с тензорами применяют много где, но это далеко не всегда является тензорами (хоть теперь это и модно так называть). Так же как когда-то в начали применять когда-то понятие «вектор» для описания коллекций объектов. Вектором из векторного анализа оно не стало.

НЛО прилетело и опубликовало эту надпись здесь

maksbotan 1 июл 2015 в 01:55

С точки зрения математика всегда конечно дико было смотреть на вот это вот «ну пусть есть индексы сверху, пусть есть снизу, будем менять их вот так, смотрите — круто». Но если людям удобно, почему нет :)
Хотя в голове все равно всплывают сопряженные пространства, тензорные произведения, базисы и прочая фигня. И интерпретация этого дела на многообразиях, связность, символы Кристоффеля… Ведь и для математики всё это имеет большое и интересное значение.
Спасибо за статью, обязательно продолжайте!

erlyvideo 1 июл 2015 в 09:48

Я честно пытался понять статью с наскока, спасибо вам за неё.

Но вы упустили самое главное и я потерял мысль: с самого начала надо написать, зачем это нужно.

К сожалению, весь университетский курс этим страдает: заставляют втупую зубрить что-то со словами «потом разберетесь, годам к 35»

maisvendoo 1 июл 2015 в 09:59

с самого начала надо написать, зачем это нужно

Учту это. Видимо главную мысль статьи мне пока не удалось сформулировать

IlyaPodkopaev 1 июл 2015 в 10:07

все же индексы вверху — порочная практика, я всю статью боролся с тем, чтобы не читать их как степень. Отделение скобками помогает…

maisvendoo 1 июл 2015 в 10:14

Тем не менее, практика принята в тензорном исчислении, и в подавляющем большинстве книг используется именно такая нотация.

Дело в том, что мы имеем дело с линейными операциями, поэтому верхнее положение индекса и не рассматривается здесь как показатель степени.

Если речь идет таки, например о квадрате компоненты, то пишут так
$a^1 \, a^1 = (a^1)^2$

IlyaPodkopaev 1 июл 2015 в 13:30

да, я так и подумал, что это общепринятое обозначение. Видимо зависит от того, какая запись принята в области, с которой сталкиваешься… К ней привыкаешь и уже не задумываешься

grossws 1 июл 2015 в 13:55

Хуже когда в рамках одной статьи (а то и выражения) верхний индекс обозначает разные вещи. В том же ML часть авторов использует верхний индекс в скобках (как номер примера для обучения) и, в том же выражении, верхний индекс без скобок (как степень). А иногда — догадывайся из контекста и обозначаний этой конкретной статьи.

НЛО прилетело и опубликовало эту надпись здесь

merlin-vrn 2 июл 2015 в 13:06

Так тогда и транспонирования в статье все нужно заменить эрмитовыми сопряжениями.

mayorovp 8 июл 2015 в 11:46

Вообще-то, до сих пор автор рассматривал только геометрические вектора — а у них координаты есть действительные числа, а не комплексные. Откуда тут возьмется сопряжение-то?

Во-вторых, вы как-то очень хитро поставили звездочку после скалярного умножения. Операция эрмитова сопряжения определена только для матриц — а результат скалярного умножения, внезапно, скаляр. Здесь надо поставить обычное комплексное сопряжение, а не эрмитово.

barmaley_exe 8 июл 2015 в 16:48

Никто не мешает считать скаляры матрицами размера 1x1.

maisvendoo 1 июл 2015 в 15:26

использована матрица А10 (как заявлено, это матрица перехода из косоугольной в прямоугольную СК)

Там написано так

Преобразование из прямоугольной системы координат в косоугольную выражается матрицей A01

что несомненно является допущенной мною опечаткой, так как матрица A01 — это матрица перехода из косоугольной в прямоугольную систему координат.

Спасибо, исправлено

НЛО прилетело и опубликовало эту надпись здесь

maisvendoo 1 июл 2015 в 16:04

Для контравариантных. Проецируем ломаную, составленную из контравариантных компонент в СК1 на соответствующую ось СК0

НЛО прилетело и опубликовало эту надпись здесь

maisvendoo 1 июл 2015 в 16:02

Кстати, в вики в статье Тензор была опечатка — векторы обозначались рангом (0, 1) а ковекторы рангом (1, 0), при том что метрический тензор указывался как (0, 2) то есть дважды ковариантный.

Взял на себя смелость внести правку — вектор (1, 0), ковектор (0, 1), согласно с источнику .

А то при разборе литературы для подготовки второй части статьи возникли нестыковки литературы и википедии…

progchip666 2 июл 2015 в 10:08

Позже, в университете, программа подготовки по моей специальности не предусматривала изучение тензорного исчисления, хотя малопонятный термин «тензор» всплывал довольно часто в некоторых специальных курсах. Например, было жутко непонятно, почему матрица, содержащая моменты инерции твердого тела гордо именуется тензором инерции.

Аналогичная ситуация сложилась у меня. Когда большая часть «Теоретиеской физики» в нашем институте была построена на тензорах, а курс матанализа данную тему обходил далеко стороной. В результате приходилось либо заучивать длинные ряды формул, либо воспринимать курс «Теорфиза» как шаманство. Ни то ни другое знаний и понимания предмета к сожалению не прибавляло.
Очень интересно будет попытаться разобраться в этом хотя бы сейчас, много лет спустя в Вашей помощью.

APXEOLOG 2 июл 2015 в 17:42

Было бы неплохо периодически говорить зачем мы начинаем те или иные преобразования. Я потерял смысловую нить уже к 5 уравнению, а когда взгляд упал на «Введем матрицу» (11), я совсем потерялся. Для меня все это выглядит как математика ради математики.

dcc0 4 июл 2015 в 21:03

Интересно, как количественно и качественно изменится понимание этого материала, если заменить терминологию? Даже было бы интересно провести такой эксперимент.
Почему-то думаю, что русский достаточен, чтобы отразить смысл, а латинизмы, которые повсеместно используются в научном мире, понимания не добавляют.

Arastas 4 июл 2015 в 23:12

Приведите, пожалуйста, 3-4 примера?

dcc0 5 июл 2015 в 00:30

Не доказано средствами самой математики, что в ней
содержатся разделы более сложные или менее сложные для восприятия человеком.
Также пока формально не доказано, что абстрактная алгебра сложнее комбинаторики, теории чисел, арифметики или иных разделов. Нет определений сложности относительного самого человека. Чем в принципе определяется сложность того или иного раздела математики для человека? Количеством разнородных операций, описанием объектов?
Не представлено формальных доказательств того, что если человек способен понять один раздел, алгебры, то он не способен понять другой.
Тут от формализма придется отступить, так как формальными средствами не доказано, что подход используемый для описания самой математики является верным или всегда верным.

Arastas 5 июл 2015 в 12:46

Спасибо, я Вас понял.

Zenitchik 5 июл 2015 в 17:08

Формальный подход к описанию — это аналог юнит-тестов. Без него математика разрушится.

dcc0 5 июл 2015 в 20:15

Слышал мнение некоторых математиков, которое заключается в следующем: «для описания математических явлений естественный язык не нужен». Вообще часто когда мы читаем какое-то новое определение, то его понимание приходит на примерах или, если хорошо владеем языком символов, то нам хватает формул. Из этого вытекает несколько вопросов педагогического характера. Можно было бы их и не озвучивать, но один все-таки повторю, этот вопрос связан с перенасыщенностью данной области знаниями терминами, в основном латинизмами. Чтобы понять, что такое тензор в математике, мне сначала приходится осознать — что есть тензор изначально, т.е. уходит много времени на осмысление корневого значения термина. Затем надо понять, почему именно в этом разделе математики употреблен именно этот термин, а не просто вектор.

erlyvideo 5 июл 2015 в 23:30

на самом деле, если разобраться, как этим пользуются физики, то всё становится гораздо понятнее и потом уже можно разобраться с формализмом.

Математики обычно отвратительно нудно и скучно рассказывают свою тему по сравнению с физиками. Но за вторыми сложно успеть.

Zenitchik 6 июл 2015 в 13:31

Я вот на счёт формализма от одного математика слышал, что теория оформляется в виде формальных определений, теорем и пр. для того, чтобы потом можно было быстро сопоставлять всё это с новыми открытиями в математике, а не думать каждый раз, что из чего и как выведено. Примерно ту же цель я преследую, когда запускаю старые юнит тесты после добавления нового функционала: быстро проверить, не поломал ли что.

dcc0 6 июл 2015 в 13:48

Вы не учитываете один момент: тот объем знаний, к которому пришла современная математика, охватывает развитие данной дисциплины за период — боюсь соврать — пусть, 2000 лет. И весь этот объем знаний предлагается усвоить человеку за период средняя школа + университет.
История математики кишит повторными открытиями одних и тех же явлений. Мне интересно лишь, изменится ли уровень знаний у выпускников, если изменить подход к преподаванию.
Ученые с многолетним опытом, конечно, не нуждаются в «математики на яблоках». Бесспорно.

НЛО прилетело и опубликовало эту надпись здесь

Zenitchik 6 июл 2015 в 14:03

Этим кишит не только история математики. Ещё интереснее бывает история биологии и палеонтологии. Многих ошибочных реконструкций (типа бродящих по дну брахиозавров) не было бы, если бы их авторы знали другие науки хотя бы в рамках школьного курса. Но как этого достичь — непонятно. То, чем не пользуешься — забывается у всех, это закономерно.
Ещё забавнее была новость о том, что биологи в начале 2000-х открыли C_y у какого-то морского гада (забыл, какого именно) — т.е. биологи XXI века удивлялись тому, что твёрдо знали братья Райт.

dcc0 6 июл 2015 в 19:17

Я, наверное, уже очень сильно отклонился от темы, в которой, конечно же, почти не ориентируюсь.
Но все же отмечу еще один момент — достаточно быстро развивается информатика, появляется
очень много терминологии, буквально каждый день. Информатика, математика и физика теперь сильно пересекаются, где-то смешиваются, и смешивается очень много терминологии, термины дополняются новыми значениями и т.д. Если можно так сказать, то терминология в общенаучном контексте превращается в некий водоворот.
В XIX веке даже еще в XX — это еще были волны, где-то предсказуемые, где не очень.

НЛО прилетело и опубликовало эту надпись здесь

dcc0 7 июл 2015 в 16:09

Я думаю, что достаточно остро в ближайшее время встанет вопрос о способах представления научной информации, под этим я подразумеваю и «сжатие»
информации для учебных целей. Думаю, это будет связано с требованиями самого времени, ведь и готовить и переподготавливать специалистов нужно довольно быстро. Во всяком случае быстрее, нежели раньше, а способы представления учебной информации пока, субъективно, к этому не очень раполагают. Думаю, это тема отдельных исследований, возможно, лингвистических по большей части. Может, найдется, наконец, интересное применение для психолингвистики.

По поводу того, является ли программирование расширением математики, сужением логики, не стану судить. Тут можно дискутировать на тему эмулируется ли математика на логическом устройстве или формальная логика реализуется на математическом.

НЛО прилетело и опубликовало эту надпись здесь

rafuck 11 июл 2015 в 09:35

У вас тут формула (21) не пронумерована, как бы абсурдно это ни звучало.
Пишу комментарием, потому что статей много, так проще.

maisvendoo 11 июл 2015 в 12:57

Не страшно, так как на (21) не ссылки в тексте. Писалось из LaTeX версии, там нумерация несколько отличалась

rafuck 12 июл 2015 в 05:51

«Подставим (22) в (21)»
Я по этой фразе заметил, что (21) нету.

maisvendoo 12 июл 2015 в 12:16

Нашел потерянную формулу. Спасибо

Alexins 25 июл 2015 в 10:35

Тут самое главное, понимание. Для чего эта сложная штука нужна. Людям проще воспринимать занимательную математику, нежели смотреть на сухие формулы тригонометрии.

Косоугольные координаты переведем в прямоугольные координаты.
Воспринимать эту штуку очень сложно по рисунку 2. Для примера, косой угол между базисами рисунка 1 больше 90 градусов. Почему нет?

Пойдем дальше. Почему точка отсчета координат одна и та же. Два объекта, находящихся в пространстве, не вложенные один в другой, являются разными точками отсчета.

Возьмем практический пример. Все мы знаем металлическую метровую линейку с дырочкой. Дырочка нужна, чтобы линейку можно было повесить на гвоздик, на стене. Вот и скажем, что дырочка, будет началом вектора. Положим линейку на пол и посмотрим на нее.
Будем условно считать себя точкой отсчета координат. По правую руку будем откладывать ось X. Вперед, куда смотрят глаза, будет координата Y. Постояли, посмотрели на линейку. Сделали несколько шагов, немного повернулись, посмотрели на линейку. Вот вам две не соосные системы координат с разными точками отсчета. В уме то мы соображаем, что линейка осталась одного размера.

Теперь возвращаемся к математике и пытаемся на пальцах объяснить что такое тензор. И как влияет изменение точки отсчета на матрицу пересчета координат вектора.

Дальше еще интереснее и вкуснее. Тут один из комментаторов приводил теорию с трансформатором. Раскладывал его на катушки и переставлял их. Продолжим его исследования и одну из катушек поставим не вертикально, как все остальные, а на бок, чтобы она каталась по столу. Вот не задача, это уже не тривиальная задача в теории катушек.
Возвращаюсь к любимым линейкам и зайдем в подъезд многоэтажного дома. Положим одну линейку на несколько ступенек пролета, идущего вверх, а вторую на несколько ступенек пролета, идущего вниз. Смотрим на линейки и думаем, как бы применить тензор к разным векторам с одинаковой длиной. И пусть сухой математик объяснит, что это суть разные вектора, а не смещение координатных пространств относительно одного вектора (метровая линейка).

НЛО прилетело и опубликовало эту надпись здесь

Alexins 26 июл 2015 в 01:09

Представим задачу с катушками более простым способом. Катушку можно представить в виде магнитной палочки из детского магнитного конструктора. Конструктор состоит из набора палочек с магнитами на концах и стальных шариков.
Одну палочку положим на гладкий стол и будем подносить конец другой палочки. Мы увидим, что палочка на столе будет поворачиваться обратной стороной магнита к палочке в нашей руке.
Усложним задачу. В руках у нас магнитная палочка, а на столе лежит катушка индуктивности, по которой не течет электрический ток. Подносим магнит. В катушке, под действием изменения внешнего магнитного поля начинает бежать электрический ток. Катушка становится магнитом и так же старается принять упорядоченное положение к магниту в нашей руке.
Изменение внешнего магнитного поля опять сказывается на образование заряда в катушке. И так действует до тех пор, пока катушка не займет определенного положения и магнитное поле для нее перестанет изменяться. В результате, в ней прекратиться выработка электрического тока и она станет инертной по отношению к магниту у нас в руке.
О таком не сложный примере, я говорил как о не самой простой задаче.
Стрелка амперметра или движение катушки диффузора динамика под действием тока внутри постоянного магнита, это одно. Я говорил о явлении наводящейся магнитной индукции.

НЛО прилетело и опубликовало эту надпись здесь

Alexins 26 июл 2015 в 16:51

Честное слово, не хочу вас обидеть. Вы кажетесь умным человеком.
Обратимся к азам катушек индуктивности. Для примера, можно посмотреть ресурс базовые формулы. В теории магнитной индукции нет места разности потенциалов и точечным зарядам. Указанный термин «распределенного электрического заряда» не очень то подходит для описания происходящих процессов.
И я, описывая пример воздействия изменяемого магнитного поля на катушку, не говорил, что она подключена к нагрузке.
Электрический ток есть, а электрического потенциала нет.
Ладно, предлагаю мир. Мы немного ушли от темы. Истина всегда где то рядом.

НЛО прилетело и опубликовало эту надпись здесь

Alexins 26 июл 2015 в 21:01

Если кому то стало интересно, в добрый путь. Основы теории электромагнитных полей являются уравнения Максвела.
Всё остальное очень тяжело воспринимается для не подготовленного человека.

На мой взгляд, математика и физика должны быть интересными и познавательными. Если удастся объяснить тяжелые вещи на простых примерах, значит вас будут слушать раскрыв рот, а не зевать во всю площадь лица.

НЛО прилетело и опубликовало эту надпись здесь

938MeV 26 июн 2019 в 20:58

Людям проще воспринимать занимательную математику, нежели смотреть на сухие формулы тригонометрии.

Теперь возвращаемся к математике и пытаемся на пальцах объяснить что такое тензор.

Занимательная математика на пальцах — это может быть не на Хабре все-таки надо делать? Зачем тогда Хабр, если на нем будет все то же самое, что и везде?

6opoDuJIo 4 авг 2015 в 04:54

Правильно ли получается, что смысл (15) -> (16) -> (17) в том, чтобы укоротить запись, а не в том, чтобы перевыразить скалярное произведение?

maisvendoo 4 авг 2015 в 11:15

(15) показывает место метрического тензора в вычислении скалярного произведения
(16) выражает связь между ковариантными и контравариантными компонентами вектора
(17) запись скалярного произведения через ковариантные компоненты одного вектора и контравариантные компоненты другого, да, по сути сокращенная запись для произвольного базиса (без использования правила Эйнштейна)

fpgaFAE 9 сен 2015 в 11:57

Здравствуйте, Дмитрий!
Вы пишете очень интересно, но, к сожалению, в оформление статьи вкрался один труднообнаруживаемый баг, который сводит все ваши труды на НЕТ: ваши формулы со временем «протухают», т.е. вместо красивой картинки с формулой со временем появляется сообщение:

Видимо, это сообщение появляется не сразу, а когда страница наберет достаточное количество просмотров, поэтому найти эту ошибку непросто.
Для исправления я могу порекомендовать надежный, но довольно трудоемкий путь: перегенерировать все формулы в картинки, загрузить эти картинки, например, на хабросторэдж и давать ссылки уже на эти картинки. Путь трудоемкий, но другого выхода я не вижу. Картинки генерируются со страницы редактирования формул по ссылке «Click here to Download Image (GIF)».

Буду рад, если вы возьмете на себя труд выполнить столь трудоемкую правку вашего текста

maisvendoo 9 сен 2015 в 18:41

Безусловно возьму на себя такой труд, тем более на первые три статьи есть черновики в LaTeX. Как только разгружусь с другими делами, а это будет в ближайшее время, буду устранять последствия катастрофы

fpgaFAE 10 сен 2015 в 13:26

Спасибо! Ситуация действительно неприятная, но работу по восстановлению можно существенно упростить, если написать несколько несложных скриптов, обрабатывающих ваши страницы. Например, все данные для формул уже забиты в строчках типа

«latex.codecogs.com/gif.latex?OB_2&space;=&space;OA_1\cos\varphi&space;+&space;OA_2&space;=&space;a^1&space;\left|\vec{e}_1&space;\right|\cos\varphi&space;+&space;a^2&space;\left|\vec{e}_2&space;\right|&space;\quad&space;(4)»

Если в них заменить latex.codecogs.com/gif.latex? на latex.codecogs.com/gif.download?, то уже набранные формулы будут сохранены в виде gif-файла. Ручная правка, конечно потребуется, но ее будет значительно меньше

6opoDuJIo 24 сен 2015 в 00:07

К счастью, как минимум часть статей остались с иллюстрациями на Wayback machine.

sanchousf 13 янв 2016 в 18:28

у меня некоторые формулы отображаются вот так
\vec{a} \cdot \vec{b} = \sum_{i=1}^3 a_i b^i \quad

mayorovp 13 янв 2016 в 18:51

Посмотрите ссылку на них. Это что-то смешное…

habrastorage.org/getpro/habr/post_images/472/e80/ee0/472e80ee0a5a3e54cd9897c8acd24062.gif%5ET&space;%5Cmathbf%7Bg%7D%5E%7B(0)%7D%5C,%5Cmathbf%7BA%7D_%7B01%7D&space;=&space;%5Cmathbf%7Bg%7D%5E%7B(1)%7D&space;%5Cquad&space;(23)

Такое ощущение, что кто-то (бот?), заливая на habrastorage картинки, залил только часть формулы :)

sanchousf 14 янв 2016 в 19:25

Скорее больше похоже что кто-то к ссылке добавил лишнего. Потому что работающие ссылки заканчиваются на .gif, а в тайтле формула, а в не работающей формула прям в ссылке.

mayorovp 14 янв 2016 в 20:12

Раньше (до загрузки на hstor) во всех ссылках были формулы — и по ним генерировалась картинка. А тут — картинка сгенерирована только по части формулы (ее видно если обрезать ссылку) — а остальная часть формулы осталась в ссылке. Потому я и подозреваю ошибку бота.

maisvendoo 2 мар 2016 в 07:59

В Формулы в статье исправлены. Постепенно откорректирую все остальные

mayorovp 2 мар 2016 в 09:18

Это временно. Придет бот и опять испортит :)

maisvendoo 2 мар 2016 в 10:25

Те статьи, что написаны с использованием ресурса Романа Парпалака остались в целости. Так что, будем надеяться, переживут

sanchousf 24 апр 2016 в 00:10

Мне все понятно с конравариантными координатами. Формула (1) даже показывает как имея контравариантые координаты и базис получить вектор.
Но мне не ясно как это сделать с ковариантными не переводя их в контравариантные? И мне интересно узнать зачем они нужны? Когда ковариантными координатами предпочтительнее пользоваться чем контравариантными?

Phaker 17 июн 2019 в 15:18

Потерялась нумерация формулы (23), хотя дальше стоит ссылка на неё.
В формуле (24) перепутаны индексы систем координат: в левой части должен быть (1), а в правой (0).

neyronon 25 ноя 2020 в 11:35

Прекрасный материал. Небольшое замечание — когда в последнем примере выражаем координаты в новом базисе, не сразу доходит, что там надо компоненты вектора умножать на компоненты обратной матрицы преобразования, которая есть «а» с волной, так как нигде не раскрывается, что волна указывает на обратное преобразование.

dfreev 12 сен 2023 в 20:01

Все-таки это математика, а не физика.

dfreev 13 сен 2023 в 20:52

Я не математик, поэтому заранее прошу извинить, если мои замечания покажутся дилетантскими.

1. Не понял: зачем в (2) входят модули ортов? Длины(!) отрезков ОА1 и ОА2 равны проекциям вектора а на оси, соответственно это а1 и а2 (как и положено длинам, они скаляры, модули ортов тут излишни). Вектора ОА1 и ОА2 выражаются через орты так, как это показано в выражении (1) (оно и представляет собой сумму этих векторов, модули опять не при чём). Вывод: формула (2) неправильная.

2. То же замечание относится к (3) и (4): если это длина проекций на оси, то орты вообще надо убрать, если это векторы проекций, надо убрать знаки модуля у ортов.

3. Необходимо указать, что в числителе (5) и (6) стоят скалярные произведения, без этого смысл формул совершенно не понятен. Их результат, в самом деле, проекция вектора на ось (скаляр). Но зачем вообще в (5) и (6) нужен знаменатель? Знаменатель должен быть удалён. Вывод: формулы (5) и (6) необходимо пояснить и исправить.

4. Иллюстрация ко- и контравариантности в 1-ом параграфе – неудачная, так как совершенно не проясняет физику этих понятий. В частности, соотношение ко- и контравариантных базисов в СТО совсем не то, что в тексте. В таком случае, что из текста мы узнаём о месте ковариантного базиса в пространстве (евклидовом, СТО, ОТО) по отношению к контравариантному базису? Похоже, что ничего.

mayorovp 13 сен 2023 в 21:20

Не понял: зачем в (2) входят модули ортов? Длины(!) отрезков ОА1 и ОА2 равны проекциям вектора а на оси, соответственно это а1 и а2 (как и положено длинам, они скаляры, модули ортов тут излишни).

Э-э-э, нет. В том-то и фокус что при увеличении модуля базисных векторов (не ортов!) координаты a¹ и a² будут уменьшаться и наоборот. Пусть формула и выглядит странной и вообще лишней — ошибок в ней нет.

То же замечание относится к (3) и (4): если это длина проекций на оси, то орты вообще надо убрать, если это векторы проекций, надо убрать знаки модуля у ортов.

То же самое, нет там ошибок.

Необходимо указать, что в числителе (5) и (6) стоят скалярные произведения, без этого смысл формул совершенно не понятен. Их результат, в самом деле, проекция вектора на ось (скаляр). Но зачем вообще в (5) и (6) нужен знаменатель? Знаменатель должен быть удалён. Вывод: формулы (5) и (6) необходимо пояснить и исправить.

То что в числителе скалярные произведения — и так очевидно, используется же общепринятое обозначение для него. А зачем знаменатели — см. прошлый пункт.

Иллюстрация ко- и контравариантности в 1-ом параграфе – неудачная, так как совершенно не проясняет физику этих понятий.

Это математические понятия, какая у них может быть физика?

В таком случае, что из текста мы узнаём о месте ковариантного базиса в пространстве (евклидовом, СТО, ОТО) по отношению к контравариантному базису?

Это ж вектора, причём тут вообще место?

dfreev 14 сен 2023 в 16:07

1. Всё-таки остаюсь при своём мнении: формулы (1) и (2) «не стыкуются» между собой. В формуле (1) е1 и е2 – это именно орты, то есть, единичные базисные вектора, задающие масштаб вдоль соответствующей оси. Произведения проекций вектора а (а1 и а2, скаляров) и ортов е1 и е2 задают векторы ОА1 и ОА2. В сумме векторы ОА1 и ОА2 дают (по правилу параллелограмма) исходный вектор а, что и отражает формула (1).

В таком случае в числителе (5) е1 тоже орт, и при скалярном произведении вектора а на единичный вектор (орт) мы получаем точное значение проекции а на ось (ОВ1, скаляр). Поэтому знаменатель избыточен.

Однако в целом ход рассуждений автора, по-моему, правильный. Если всё подкорректировать, в итоге всё равно должен получиться метрический тензор (11).

2. Математика описывает количественные взаимосвязи и законы природы в окружающем нас реальном мире, в отрыве от него она не существует. Поэтому рискну утверждать, что любому абстрактному математическому объекту можно найти физическую иллюстрацию, пусть даже не менее абстрактную (типа десятимерного пространства). Автор и сам не ограничивается формулами, а сопровождает их рисунками – это и есть физическая (геометрическая) интерпретация. Конкретно: автор указал на место ковариантного базиса в косоугольных координатах (хотя и не акцентировал этот момент). Где он локализуется в СТО, известно. Если бы уважаемые математики рассказали нам, где он прячется в ОТО, а потом обобщили на все «случаи жизни», они сильно облегчили бы жизнь всем остальным: по-моему, непонимание тензорного исчисления (в частности, ковариантности, свёртки, «жонглирования» индексами и т. п.) объясняется именно отсутствием понятных физических интерпретаций. Поэтому всё сказанное здесь не «философия», а самая что ни на есть «проза жизни». А вопрос остаётся: какой смысл в очередной раз излагать тензорное исчисление без «физики»?

mayorovp 14 сен 2023 в 20:15

В формуле (1) е1 и е2 – это именно орты, то есть, единичные базисные вектора, задающие масштаб вдоль соответствующей оси.

Нет. В формуле (1) е1 и е2 — вектора произвольного базиса. Они не обязаны быть единичными!

Конкретно: автор указал на место ковариантного базиса в косоугольных координатах (хотя и не акцентировал этот момент). Где он локализуется в СТО, известно. Если бы уважаемые математики рассказали нам, где он прячется в ОТО

Он не "локализуется" и не "прячется" нигде, это инструмент который, при желании, можно применить где угодно.

Кстати, ковариантных базисов не бывает. Бывают ковариантные координаты в некотором базисе.

dfreev 15 сен 2023 в 16:06

Уважаемый mayorovp!

1. В моём понимании базисный вектор – это «стрелка», уходящая за границы видимой Вселенной. Он не имеет количественного измерения и по этой причине не может входить в уравнения типа (1), описывающего количественные взаимосвязи. В уравнениях типа (1) могут фигурировать только орты.

2. «Ковариантный базис» является синонимом «дуального базиса». Само название дуального базиса говорит о том, что он противопоставляется некоему исходному базису – контравариантному. Впрочем, в математике противопоставление этих базисов чисто условное, их можно менять местами. (В этом с Вами следует согласиться). Но в любом случае это не один базис, это разные базисы. Иллюстрация: в СТО ко- и контравариантный базисы совершенно разные, у них совпадают только временнЫе координатные оси.

3. Здравый смысл заставляет не допускать абсолютной уверенности в собственной правоте, поэтому хотелось бы услышать мнение автора по обсуждаемым вопросам.

mayorovp 15 сен 2023 в 17:07

Уважаемый dfreev! Вы сами написали, что вы — не математик. Так почему вы пытаетесь перекрыть своим представлением не-математика математическое определение?

А говорит это определение, что базисом называется линейно независимый набор векторов, с помощью линейных комбинаций которых можно представить любой другой вектор. Единичности размеров векторов определение не требует, как бы вам не хотелось иного.

Если вы физик, то можете считать что базисные вектора задают ещё и единицы измерения.

dfreev 15 сен 2023 в 17:58

Я понял, в чём суть разногласий. Я обсуждал формулы (1) и (2), а Вы – определение базиса. Ну, определение Вы дали, спасибо за это. В продолжении дискуссии не вижу смысла.

mayorovp 15 сен 2023 в 19:15

Формула (1) — это и есть часть определения базиса, а формула (2) из него следует. Но если вы этого не видите — то в продолжении дискуссии и правда нет смысла.

dfreev 16 сен 2023 в 18:54

Разобрался. Признаю: был неправ. Суть в том, что базисный вектор всегда выступает в качестве меры длины, но он не обязан быть единичным.

usr345 26 сен 2023 в 10:37

Уважаемый автор, читаю текст:

Выражение (12) дает связь между ковариантными и контрaвариантными координатами вектора, определяемую лишь видом матрицы g, зависящей от длин взаимного расположения базисных векторов.

Мне кажется, что фраза "зависящей от длин взаимного расположения базисных векторов" звучит бессмысленно. Что такое "длина взаимного расположения"? Учитывая, что элементами матрицы являются скалярные произведения векторов, возможно вы имели в виду "от длин и взаимного расположения базисных векторов"?

VAK_53 21 янв в 20:53

В формуле (1.21) нельзя произвести умножение матриц, т.к.

при умножении число столбцов левой матрицы д.б. равно числу строк правой матрицы,

a и в - матрицы столбцы контрвариантных координат,

g - матрица 3х3.

Никак не получается, хоть начинать с a на g, хоть с g на b. Да и в матрицах закон ассоциативности действует.

VAK_53 21 янв в 21:21

Прошу извинения. Не заметил значка транспонирования колонки в строку.

Зарегистрируйтесь на Хабре, чтобы оставить комментарий

Erwinmal 8 часов назад
«Не трогай оливье, это на Новый год!»: немного об истории самого культового и мемного блюда новогоднего стола
Простой
12 мин
2.2K
Ретроспектива
+37
23
+23
otie173 20 часов назад
Odinbit, продолжение разработки своей игры. Новые механики, оптимизации, появление мультиплеера
Простой
6 мин
2.1K
+30
4
+4
DimDimDimDimDim 9 часов назад
Seagate представляет 32 ТБ накопитель для пользователей: технология HAMR идет в массы
4 мин
2.5K
+23
9
+9
butuzoff_ya 6 часов назад
Как я разрабатывал хоррор-стратегию на Game Maker, что из этого вышло + пара советов
Простой
6 мин
1.6K
Кейс
+15
12
+12
GeeksCat 10 часов назад
Бегущий по флешбэкам
Простой
11 мин
672
Ретроспектива
+10
5
+5
Catx2 6 часов назад
Космический интернационал
40 мин
984
+9
2
+2
Andrey2008 9 часов назад
PVS-Studio соответствует требованиям ГОСТ Р 71207—2024 (статический анализ программного обеспечения)
Сложный
71 мин
930
Обзор
+8
2
+2
bodyawm 3 часа назад
Как китайцы «айфон на винде» сделали: Смотрим на Meizu M8
Простой
8 мин
1.5K
Ретроспектива
+6
8
+8
gonzazoid 4 часа назад
Как Ultimatum помогает бороться со слежкой в сети
Простой
3 мин
1.2K
+6
3
+3
Sivchenko_translate 5 часов назад
Оптимизация компилятора на пальцах
15 мин
778
Перевод
+6
2
+2

Веб-дизайн 3.0
По факту набораSkillbox
Adobe Illustrator с нуля
По факту набораБруноям
Графический дизайнер: старт карьеры
По желаниюСодействие занятости
Основы Adobe Illustrator
По факту набораCoddyschool
Photoshop для иллюстраторов
По факту набораSkillbox

Магия тензорной алгебры: Часть 1 — что такое тензор и для чего он нужен?

Содержание

Введение

1. Вектор на плоскости. Контравариантные, ковариантные координаты и связь между ними

2. Скалярное произведение векторов

3. Правило Эйнштейна

4. Анализ на простых примерах

5. Преобразование метрического тензора при смене базиса

Заключение и выводы

Редакторский дайджест

Комментарии 89

Публикации

«Не трогай оливье, это на Новый год!»: немного об истории самого культового и мемного блюда новогоднего стола

Odinbit, продолжение разработки своей игры. Новые механики, оптимизации, появление мультиплеера

Seagate представляет 32 ТБ накопитель для пользователей: технология HAMR идет в массы

Как я разрабатывал хоррор-стратегию на Game Maker, что из этого вышло + пара советов

Бегущий по флешбэкам

Космический интернационал

PVS-Studio соответствует требованиям ГОСТ Р 71207—2024 (статический анализ программного обеспечения)

Как китайцы «айфон на винде» сделали: Смотрим на Meizu M8

Как Ultimatum помогает бороться со слежкой в сети

Оптимизация компилятора на пальцах

Минуточку внимания

Читают сейчас

После 15 декабря начались массовые сбои в работе VPN и zapret, discord и youtube перестали нормально работать

Трафик YouTube в РФ за несколько дней упал ещё на 10%

WhatsApp, Skype, Wire, Element, KakaoTalk, DUST, Keybase, Trillian, Status и Crypviser внесены в реестр ОРИ РКН

Пользователи из РФ массово жалуются на проблемы с YouTube — сайт\приложение загружается, но видео не запускается

11 мифов о поиске работы в IT и что о них думают работодатели

Истории

Ближайшие события

Магия тензорной алгебры: Часть 1 — что такое тензор и для чего он нужен?

Содержание

Введение

1. Вектор на плоскости. Контравариантные, ковариантные координаты и связь между ними

2. Скалярное произведение векторов

3. Правило Эйнштейна

4. Анализ на простых примерах

5. Преобразование метрического тензора при смене базиса

Заключение и выводы

Редакторский дайджест

Конференции, хакатоны, митапы: что посетить в декабре

Витаем в облаках: новый хаб для облачных разработчиков

Боли стартапов и акселерация: выводим MVP на рынок