(cache)マクスウェル方程式の意味を分かりやすく解説！［イメージで理解］

誠に勝手ながら、当サイトは2024年10月末をもちまして閉鎖させていただくことになりました。長らくのご愛顧に心より感謝申し上げます。

本記事の内容

本記事では、マクスウェル方程式（Maxwell's equation）について解説しています。

マクスウェル方程式

\begin{aligned} (1) & \nabla \times E & = - \frac{\partial B}{\partial t} \\ (2) & \nabla \times H & = J + \frac{\partial D}{\partial t} \\ (3) & \nabla \cdot D & = ρ \\ (4) & \nabla \cdot B & = 0 \end{aligned}

各式の変数はそれぞれ以下を意味します。

{\begin{cases} E : & 電界 [V / m] = [N / C] \\ B : & 磁束密度 [T] = [Wb / m^{2}] \\ H : & 磁界 [A / m] \\ D : & 電束密度 [C / m^{2}] \\ J : & 電流密度 [A / m^{2}] \\ ρ : & 電荷密度 [C / m^{3}] \end{cases}

本記事では、マクスウェル方程式の物理的な意味と各式から導出される法則について解説します。

$\nabla \times E = - \frac{\partial B}{\partial t}$

解釈

磁束密度 $B$ の時間変化（右辺）によって、電場 $E$ の回転（左辺）が生じることを表しています。

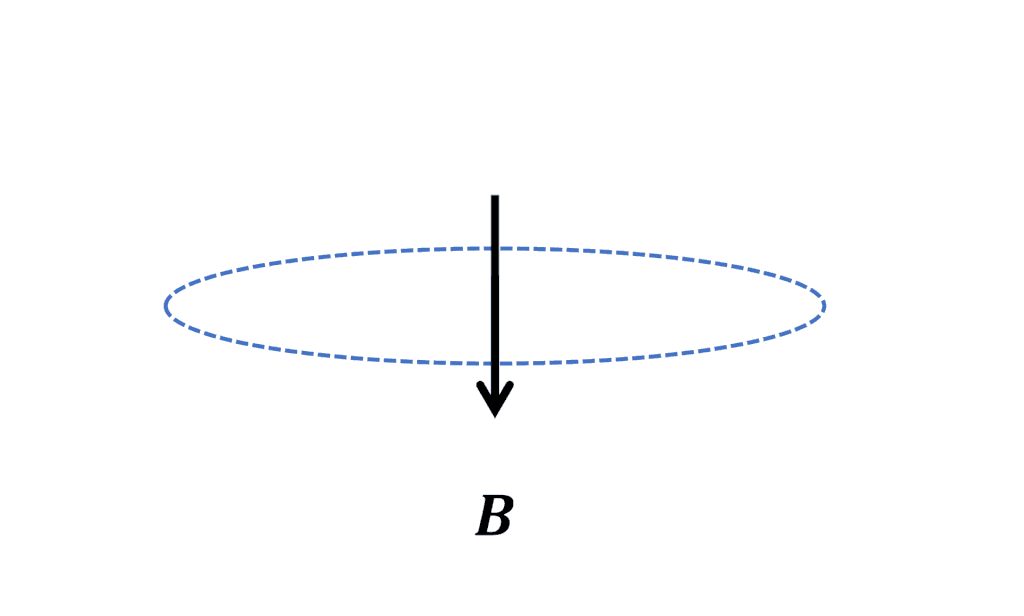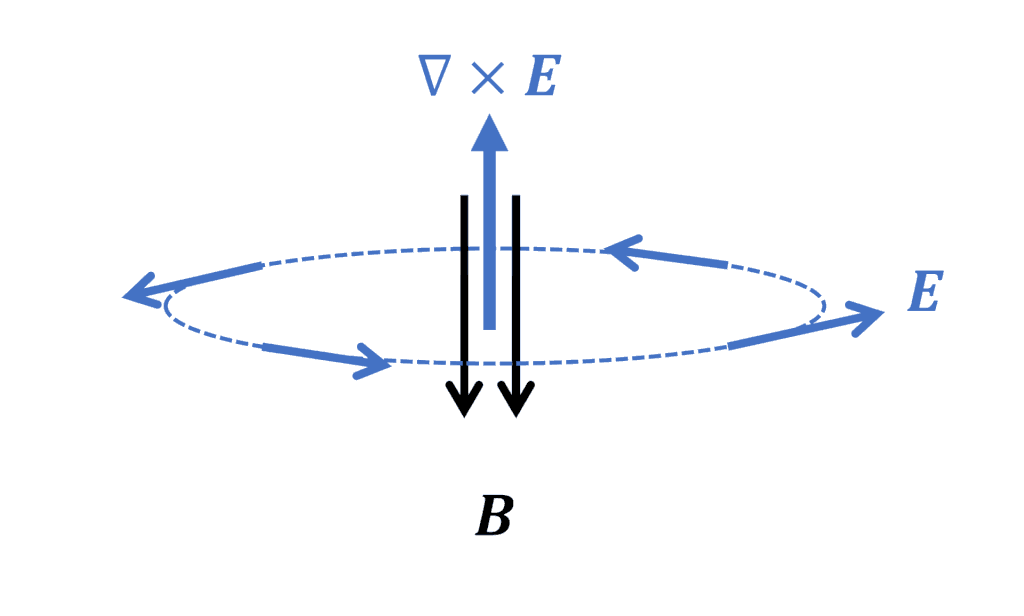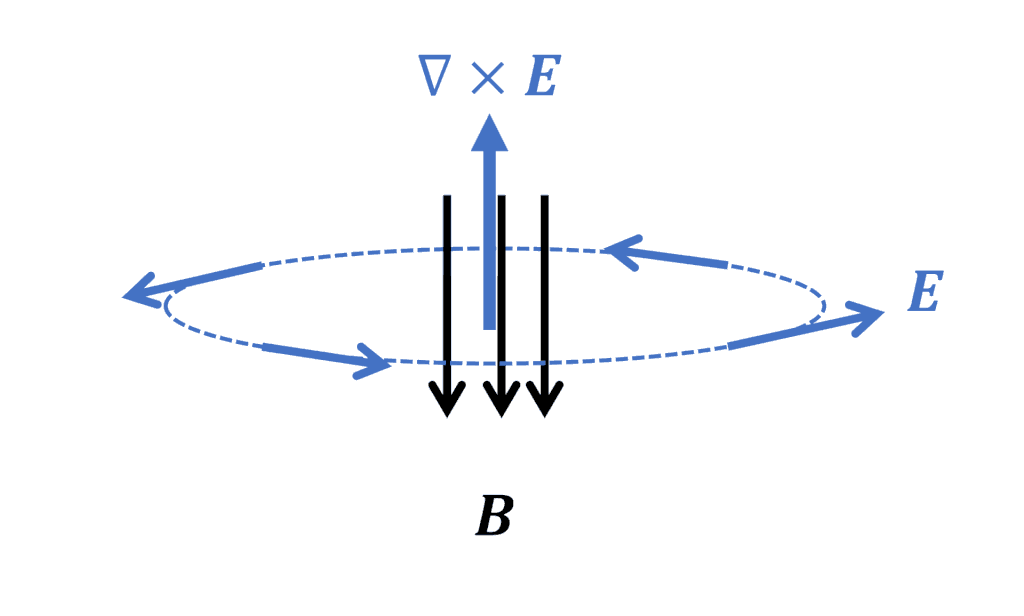
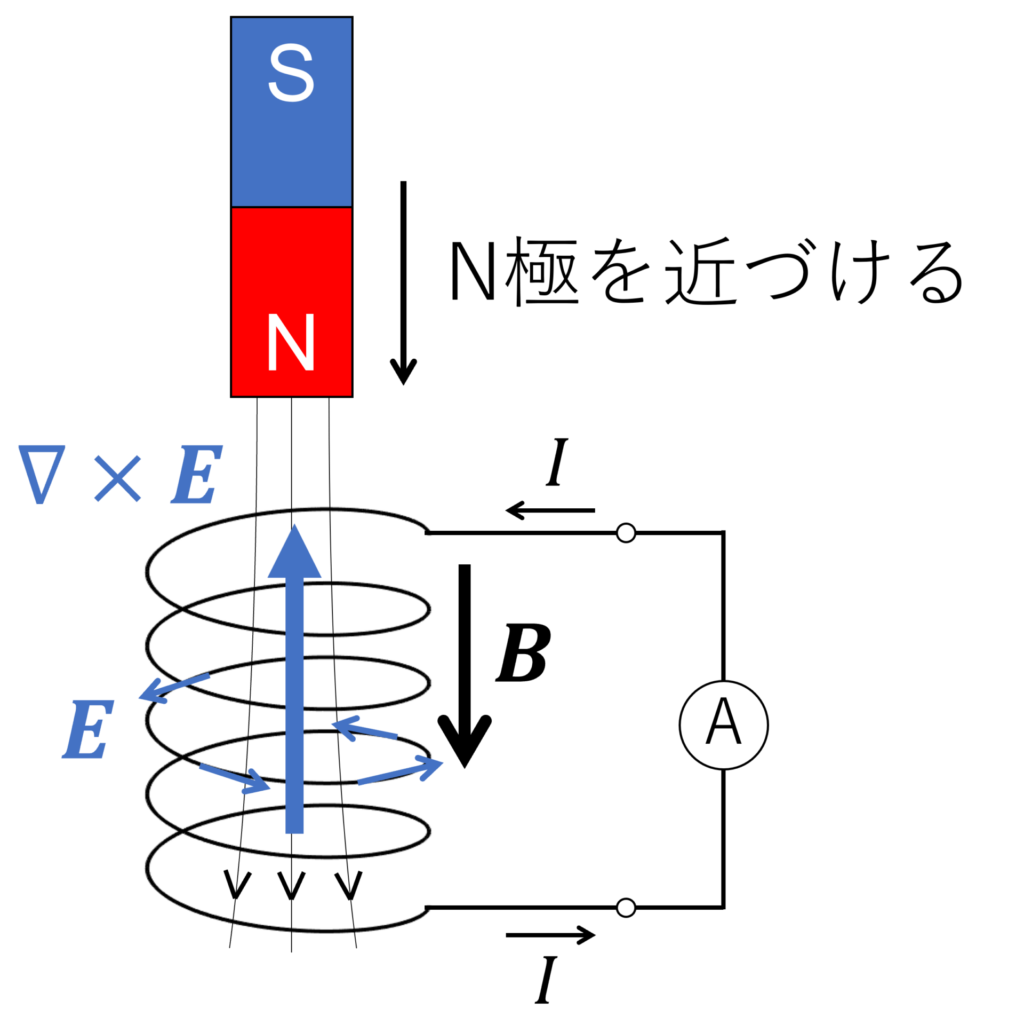
右辺にマイナスがついているので、電場の回転 $\nabla \times E$ の向きは、時間変化する磁束密度の向きと逆向きになります。これは、中学や高校で習った電磁誘導に相当します。

上図は、電磁誘導を確かめる実験（外部リンク）の概要図です。図のように、磁石のN極側をコイルに近づけると、コイルの空洞を通る磁束密度が時間とともに増加します（ $| \partial B / \partial t | > 0$ ）。すると、 $B$ と逆向きに電場の回転 $\nabla \cdot E$ が生じます。図では、 $\nabla \cdot E$ は上向きで、電場 $E$ は上向きを進行方向としたときの右ねじを回す方向に生じます。生じた電場によって、コイル内の電荷は力を受けて動き、電流が流れだします。

ファラデーの電磁誘導の法則

1.1節で説明した通り、式 $(1)$ は電磁誘導を表します。ここでは、コイルに生じる誘導起電力を導出します。

\begin{matrix} (1) & \nabla \times E = - \frac{\partial B}{\partial t} \end{matrix}

両辺、面積分をして、

\begin{matrix} (1-1) & \int_{S} \nabla \times E \cdot d S = - \frac{\partial}{\partial t} \int_{S} B \cdot d S = - \frac{\partial ϕ}{\partial t} \end{matrix}

ここで、磁束 $ϕ [Wb]$ は、磁束密度の面積分で与えられます。つまり、

\begin{matrix} (1-2) & ϕ = \int_{S} B \cdot d S \end{matrix}

式 $(1-1)$ の左辺について、ストークスの定理を適用すると、誘導起電力 $e$ は

\begin{matrix} (1-3) & \int_{S} \nabla \times E \cdot d S = \oint_{C} E \cdot d s = e \end{matrix}

ただし、 $C$ は面積分の領域 $S$ の外周に沿った積分路を表します。以上、式 $(1-1)$ ～ $(1-3)$ より、ファラデーの電磁誘導の法則が導かれます。

ファラデーの電磁誘導の法則

e = - \frac{d ϕ}{d t}

電圧則

キルヒホッフの電圧則（Kirchhoff's Voltage Law: KVL）は、式 $(1)$ から導くことができます。ここでは、磁界に時間変化がない場合（静磁界）を考えます。このとき、式 $(1)$ は

\begin{matrix} (1-4) & \nabla \times E = 0 \end{matrix}

となります。式 $(1-4)$ の両辺を面積分し、ストークスの定理を適用すると、

\int_{S} \nabla \times E \cdot d S = \oint_{C} E \cdot d s = 0

を得ます。ここで、 $C$ は回路に沿った積分路を表します。

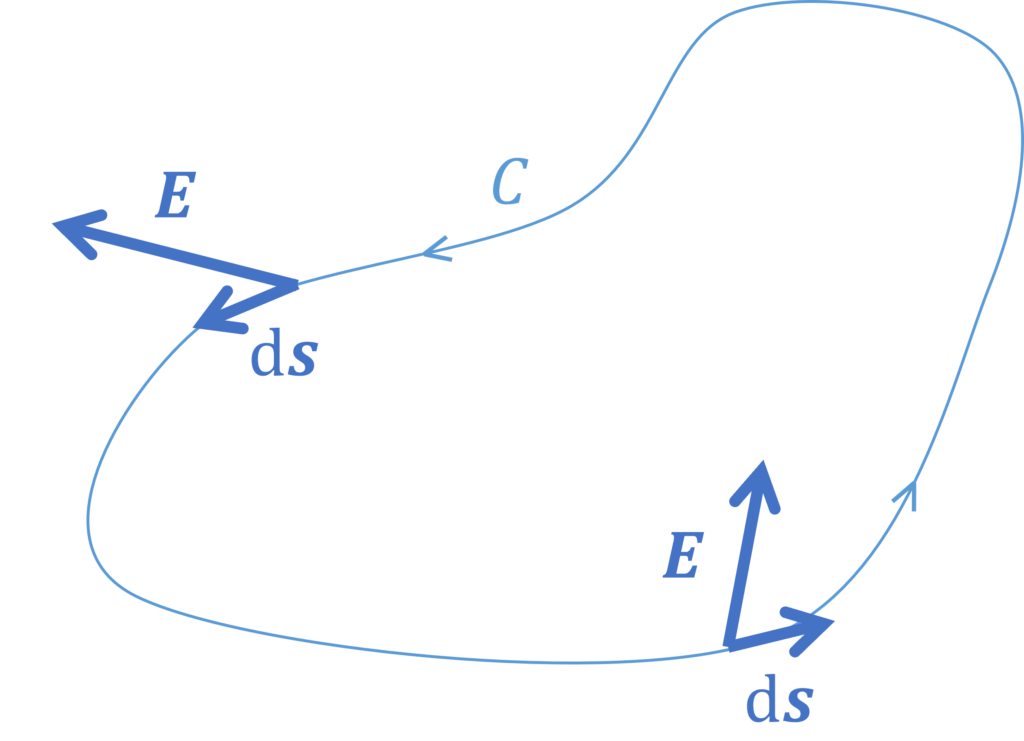
電場の線積分は電圧降下を意味するので、この式は電圧則に相当します。

電圧則

\oint_{C} E \cdot d s = 0

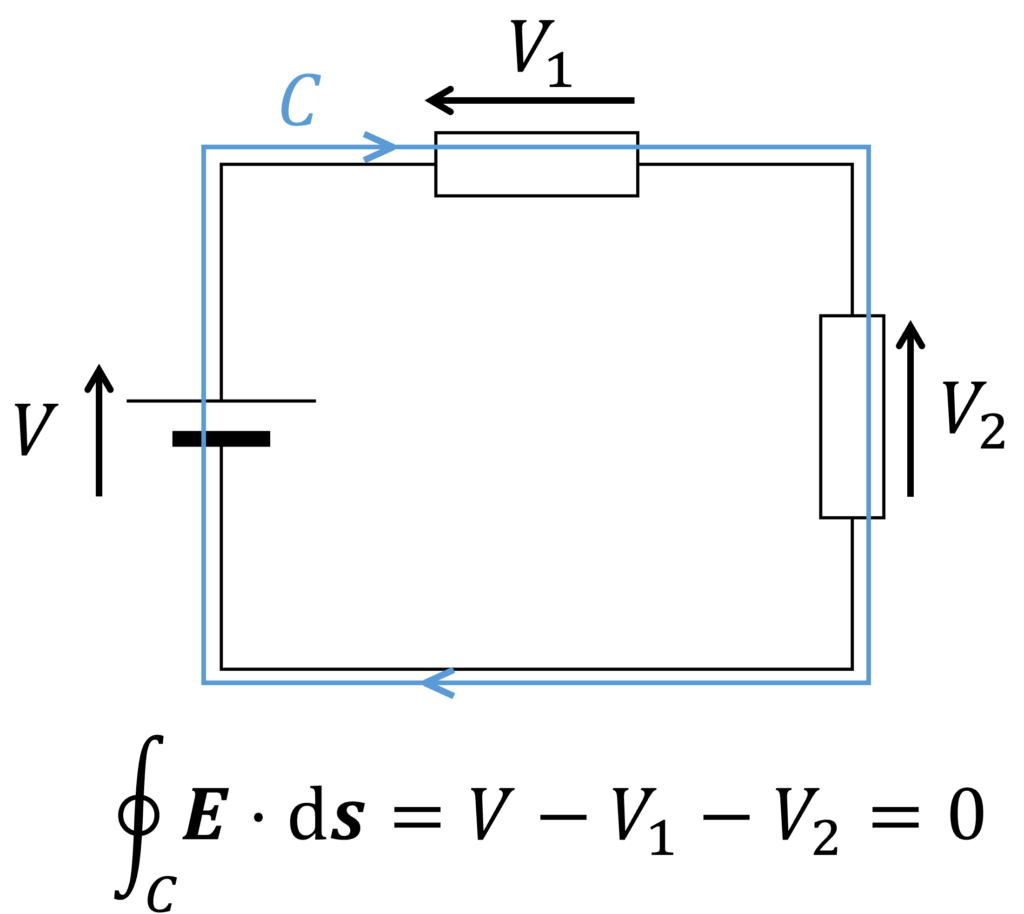
交流信号を電源として用いた場合は、電圧・電流が時間変化するため、式 $(1)$ の右辺は $0$ になりません。しかし、交流信号の波長が回路の物理的なサイズに比べて十分大きい場合、時間変化の影響はほとんど現れないため、右辺は $0$ とみなすことができます。このときの回路を集中定数回路といいます。対して、交流信号の周波数が高い、すなわち回路の大きさに対して波長の長さが短く無視できない場合は、分布定数回路として扱う必要があり、式 $(1)$ の右辺も考慮する必要があります。

$\nabla \times H = J + \frac{\partial D}{\partial t}$

解釈

電流 $J$ と電束密度 $D$ の時間変化（右辺）によって、磁界 $H$ の回転（左辺）が生じることを意味します。

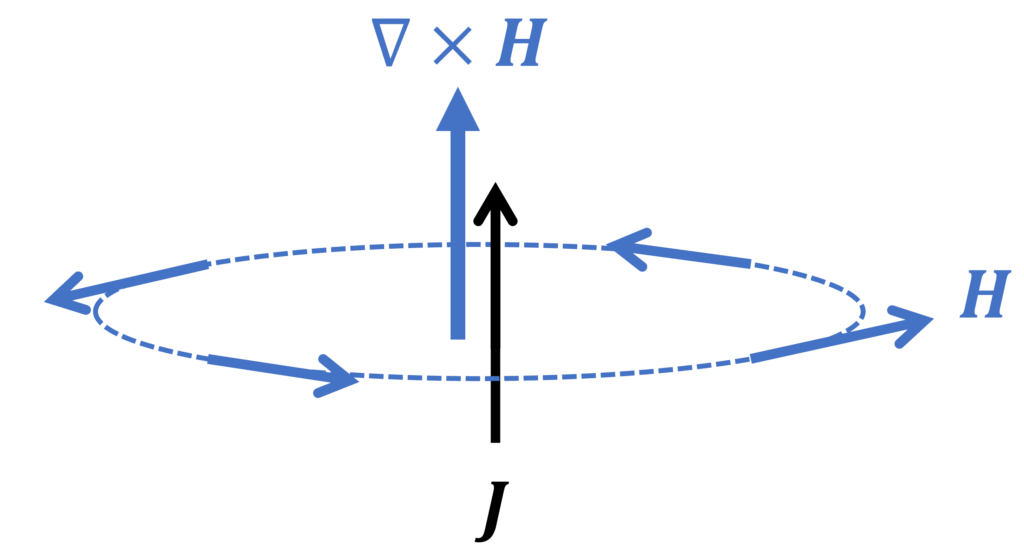
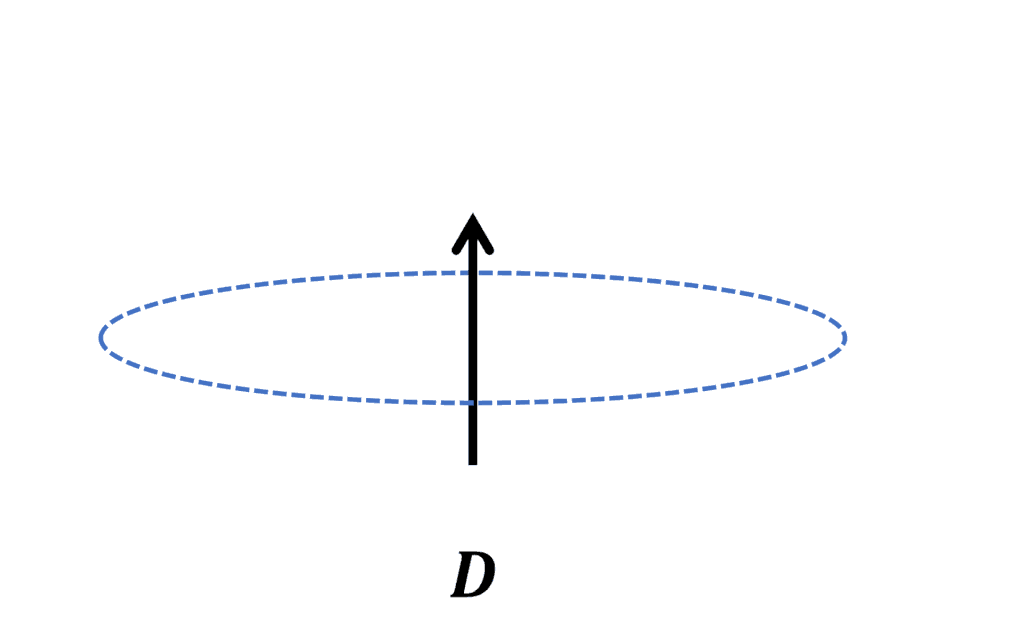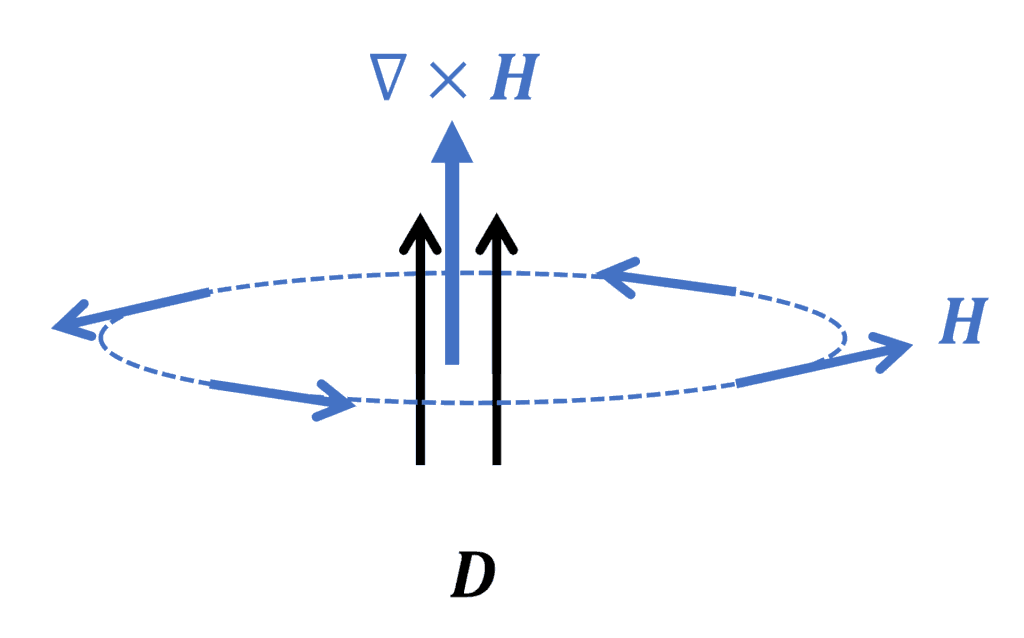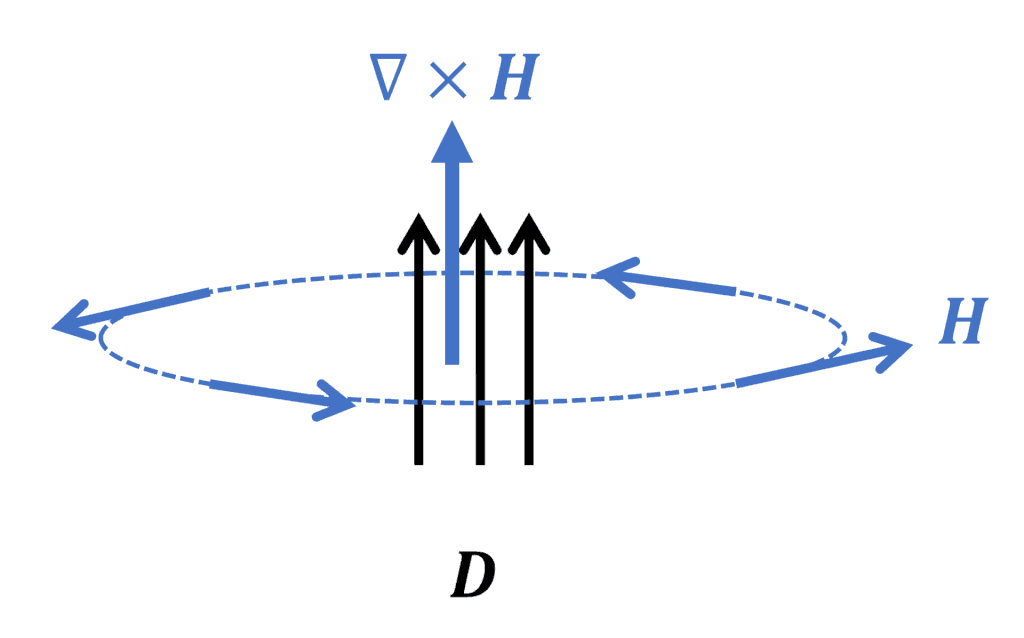
右辺の2項について、それぞれ分けて解説します。まず、右辺第2項を無視して

\nabla \times H = J

これは、直線上の導線の周囲に方位磁石を配置し、その導線に電流を流すと、方位磁石の針が電流の流れる向きに右ねじを回す方向を向くという実験（外部リンク）に相当します。

続いて、式 $(2)$ の右辺第2項について考えましょう。ここでは、 $J = 0$ として、

\nabla \times H = \frac{\partial D}{\partial t}

$\partial D / \partial t$ は変位電流と呼ばれ、見かけの電流を意味しています。

変位電流の例として、コンデンサを含んだ回路を用いて説明します。コンデンサは2つの金属板を近接させた素子で、その間には絶縁体などが挟まれています。そのため、電荷はコンデンサを直接通過することができません。

ここで、図のような回路を考えてみましょう。

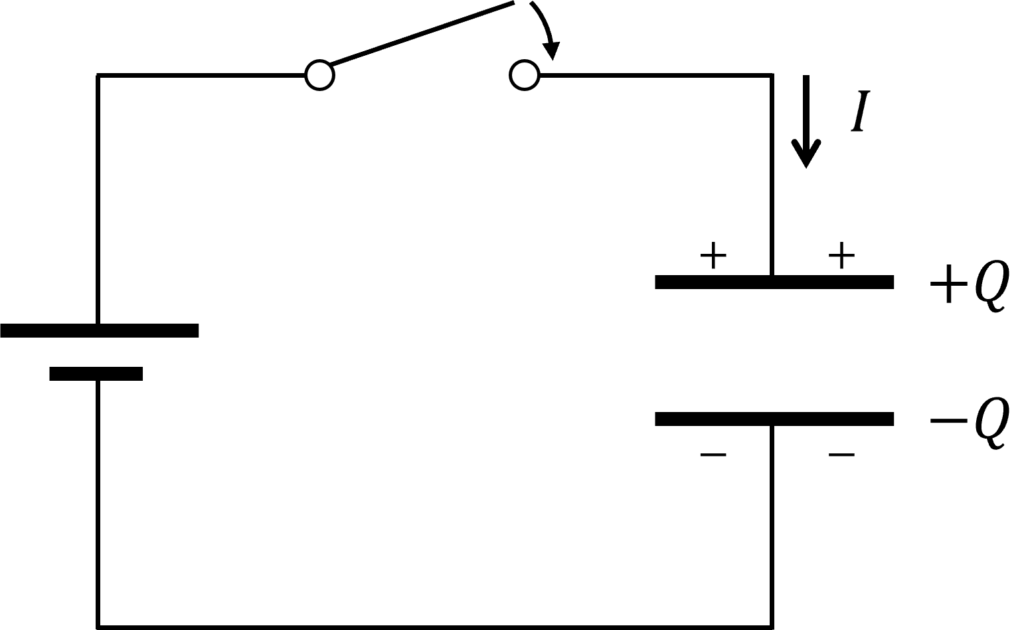
スイッチをONにすると、この回路には確かに電流が流れ、電源電圧とコンデンサにかかる電圧が等しくなるまで、コンデンサに電荷が蓄積します。では、なぜ物理的に導体が接続されていない回路に電流が流れたのでしょうか。これに説明を与えるのが、変位電流の項です。

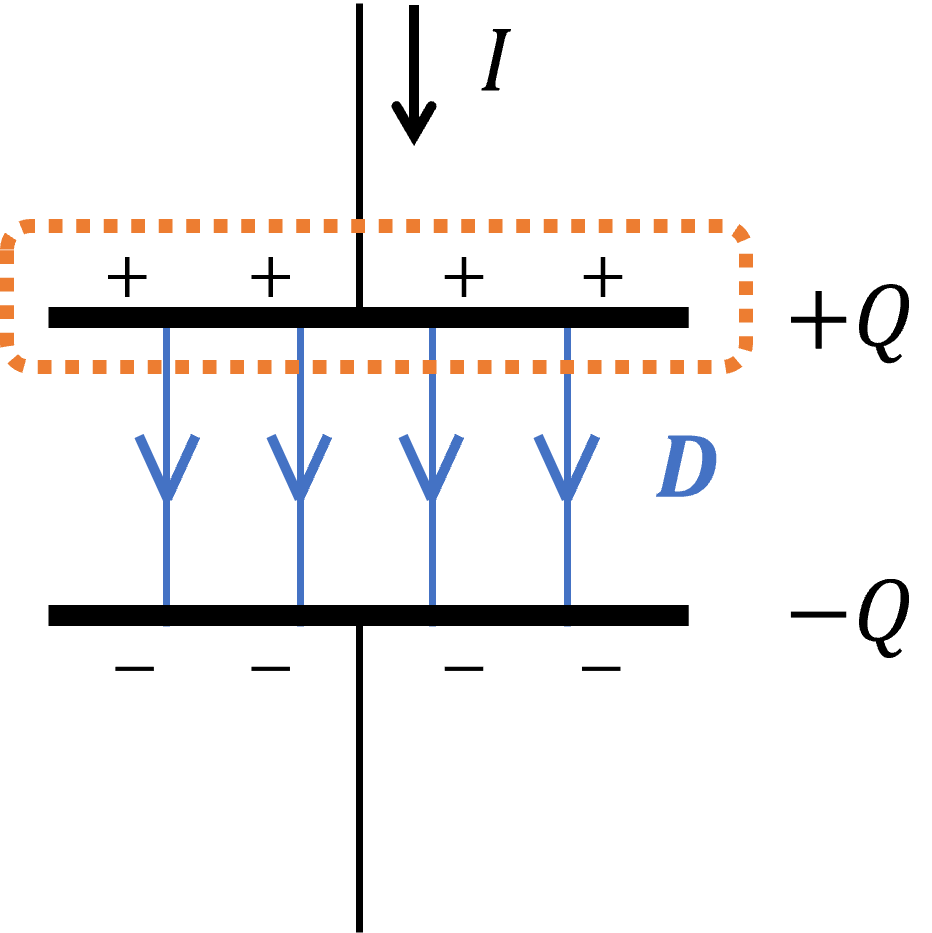
コンデンサの片方の金属板を囲む領域について、面積分を考えると、ガウスの法則より、

\int_{S} D \cdot d S = D A = Q

が成立します。ここで、金属板間の電束密度 $D$ は場所に依らないものとし、金属板の面積を $A$ , 電荷を $Q$ としました。

両辺を時間微分すると、コンデンサに流れ込む電流を $I$ として、

\frac{\partial D}{\partial t} A = \frac{\partial Q}{\partial t} = I

が成り立ちます。この式を見ると、確かに、 $\partial D / \partial t$ は電流密度の次元になっていることがわかります。このように、電荷の移動ではなく、電荷の蓄積によって生じた電流であることから、変位電流と呼ばれています。

アンペアの周回積分の法則

アンペアの周回積分の法則も、式 $(2)$ から導出されます。ここでは、静電界・静磁界を考えて、 $\partial D / \partial t = 0$ とします。

\nabla \times H = J

両辺を面積分して

\int_{S} \nabla \times H \cdot d S = \int_{S} J \cdot d S = I

ただし、積分領域に流れる電流を $I$ としました。左辺について、ストークスの定理を適用することで、アンペアの周回積分の法則を得ます。

アンペアの周回積分の法則

\oint_{C} H \cdot d s = I

電流則

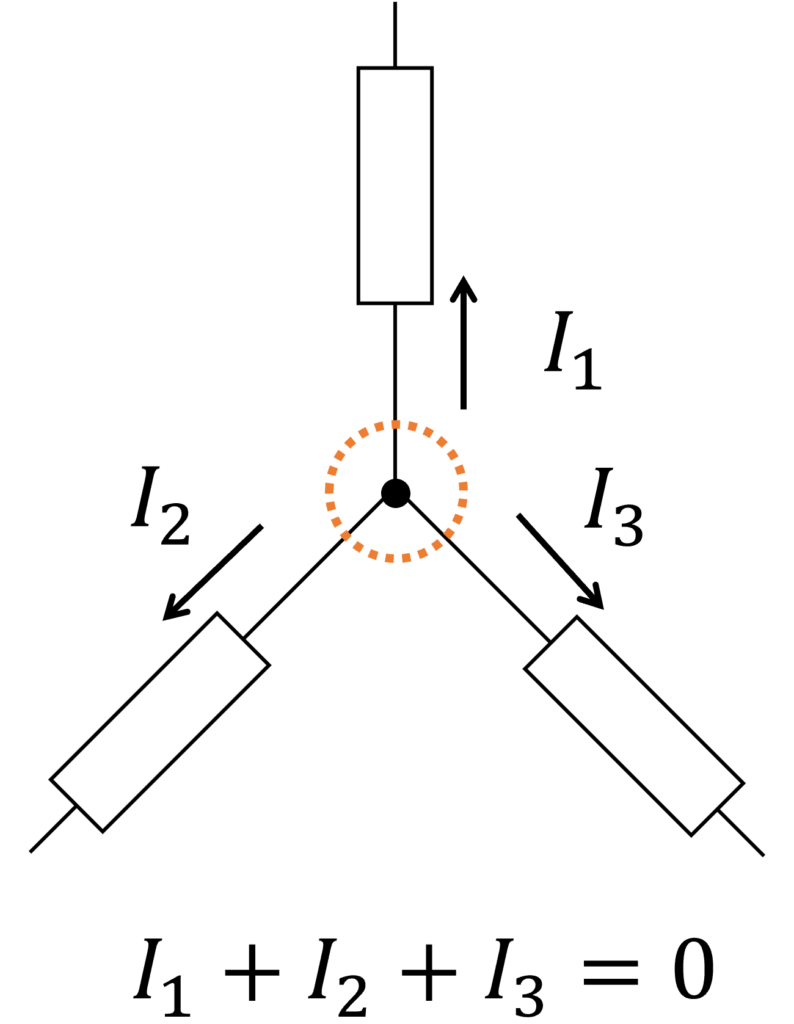
キルヒホッフの電流則（Kirchhoff's Current Law: KCL）は、式 $(2)$ より導出されます。ここでは、静電界を考えて、 $\partial D / \partial t = 0$ とします。ベクトル解析より、以下が恒等的に成り立ちます。

\nabla \cdot \nabla \times H = 0

右辺について考えると、

\nabla \cdot J = 0

これは、任意の領域からの電流の湧き出しが $0$ であることを意味しています。

電荷保存則

2.3節で導出した電流則は、2.1節で議論したように、コンデンサの片方の金属板に関しては成立しません（ $\nabla \cdot J < 0$ ）。これに説明を与えるのが電荷保存則になります。2.3節と同様に、ベクトル解析の恒等式より、

\nabla \cdot \nabla \times H = 0

このとき右辺は、

\begin{aligned} \nabla \cdot (J + \frac{\partial D}{\partial t}) & = 0 \\ \Leftrightarrow \nabla \cdot J + \frac{\partial}{\partial t} \nabla \cdot D & = 0 \end{aligned}

式 $(3)$ より、以下の電荷保存則を得ます。

電荷保存則

\nabla \cdot J + \frac{\partial ρ}{\partial t} = 0

このままでもいいですが、もう少しだけ変形してみます。両辺を体積積分して、

\begin{aligned} \int_{v} \nabla \cdot J d v + \frac{\partial}{\partial t} \int_{v} ρ d v = 0 \\ \Leftrightarrow & \int_{S} J \cdot d S + \frac{\partial Q}{\partial t} = 0 \\ ∴ & I + \frac{\partial Q}{\partial t} = 0 \end{aligned}

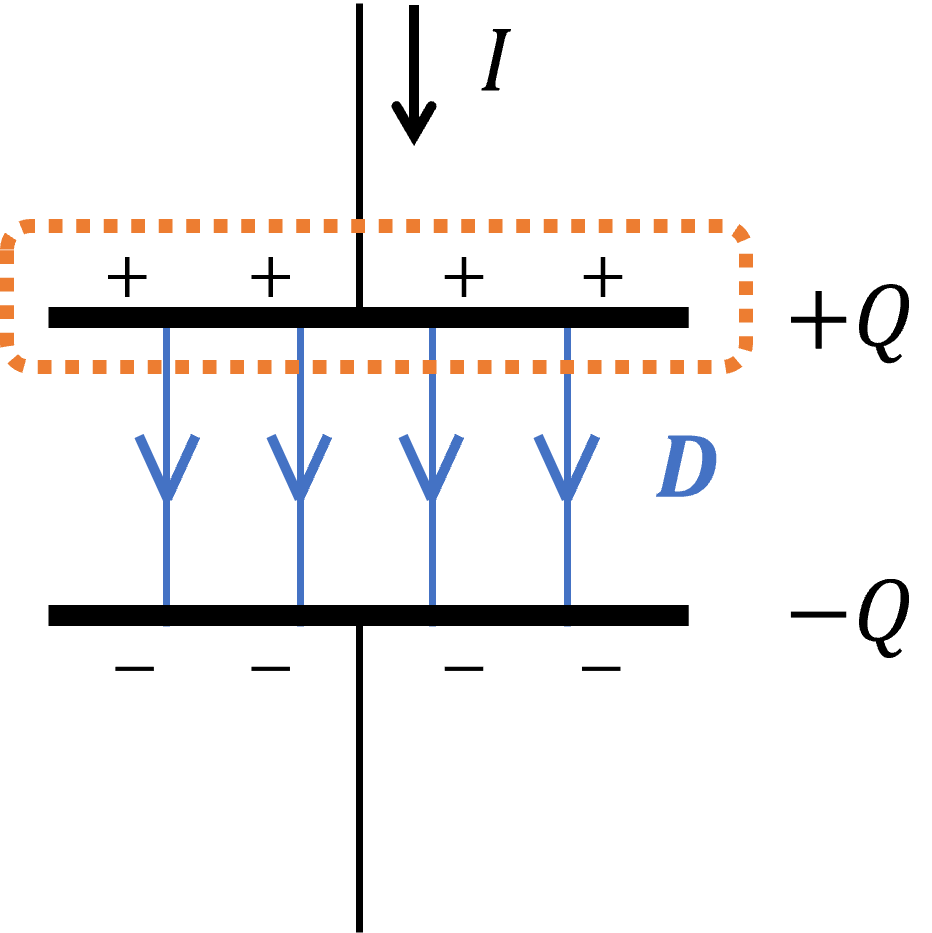
を得ます。電荷がコンデンサに蓄積しているとき、 $\partial Q / \partial t > 0$ です。また、電流 $I$ は積分領域から出る方向を $+$ に取っていることに注意すると、 $I < 0$ なので、電荷保存則と矛盾していません。

$\nabla \cdot D = ρ$

解釈

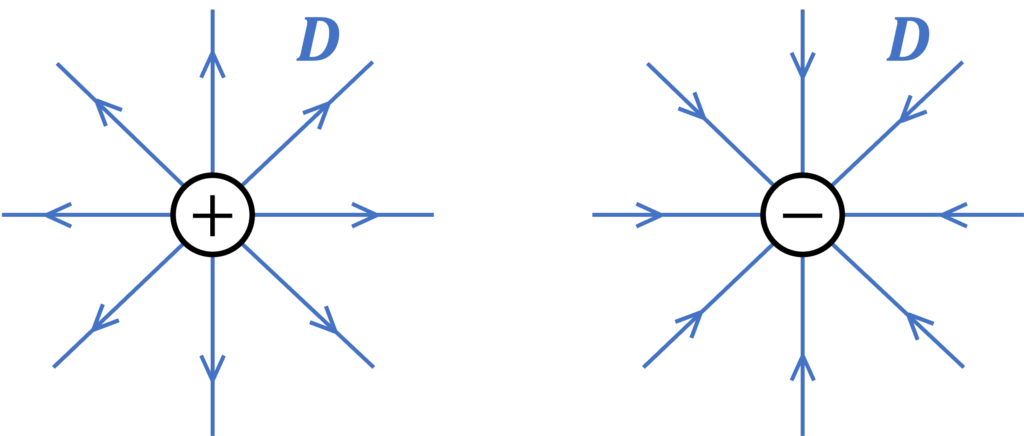
電荷から電場の湧き出しがあることを意味しています。正電荷の場合は湧き出し、負電荷の場合は吸い込みになります。

ガウスの法則

\begin{matrix} (3) & \nabla \cdot D = ρ \end{matrix}

式 $(3)$ はガウスの法則の微分形に相当します。これを、面積分の形にしてみましょう。両辺を体積積分して、

\int_{v} \nabla \cdot D d v = \int_{v} ρ d v = Q

ここで、 $Q$ は積分領域内の電荷の代数和を表します。ガウスの発散定理より、

\int_{v} \nabla \cdot D d v = \int_{S} D \cdot d S = Q

ただし、 $S$ は積分領域の表面です。よって、以下のガウスの法則を得ます。

ガウスの法則

\int_{S} D \cdot d S = Q

$\nabla \cdot B = 0$

解釈

単独の磁荷なるものが存在しないことを意味しています。

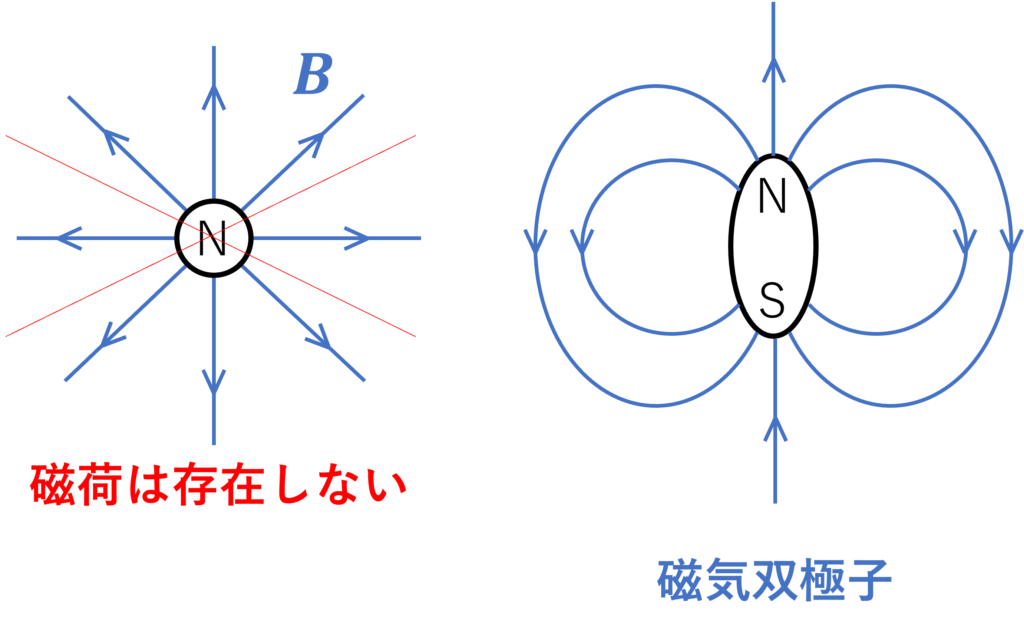
正電荷・負電荷はそれぞれ単独で存在しています。対して、N極の磁荷・S極の磁荷なるものは存在せず、N極とS極のセットで存在します。よって、空間上の任意の領域における磁場の湧き出し量は、領域に入る量と出る量が相殺されて $0$ になります。ちなみに、N極とS極のセットは磁気双極子（magnetic dipole）とよばれます。

参考サイト

ミツノ理科室, "電磁誘導でLEDを光らせる", Youtube <https://youtu.be/ANWwXNEWa_A>（参照日：2022年2月6日）
ミツノ理科室, "よくわかる！電流が作る磁場の実験", Youtube <https://youtu.be/sF9Csaplg3U>（参照日：2022年2月6日）

マクスウェル方程式の意味を分かりやすく解説！［イメージで理解］

∇×E=−∂B∂t

解釈

ファラデーの電磁誘導の法則

電圧則

∇×H=J+∂D∂t

解釈

アンペアの周回積分の法則

電流則

電荷保存則

∇⋅D=ρ

解釈

ガウスの法則

∇⋅B=0

解釈

参考サイト

$\nabla \times E = - \frac{\partial B}{\partial t}$

$\nabla \times H = J + \frac{\partial D}{\partial t}$

$\nabla \cdot D = ρ$

$\nabla \cdot B = 0$