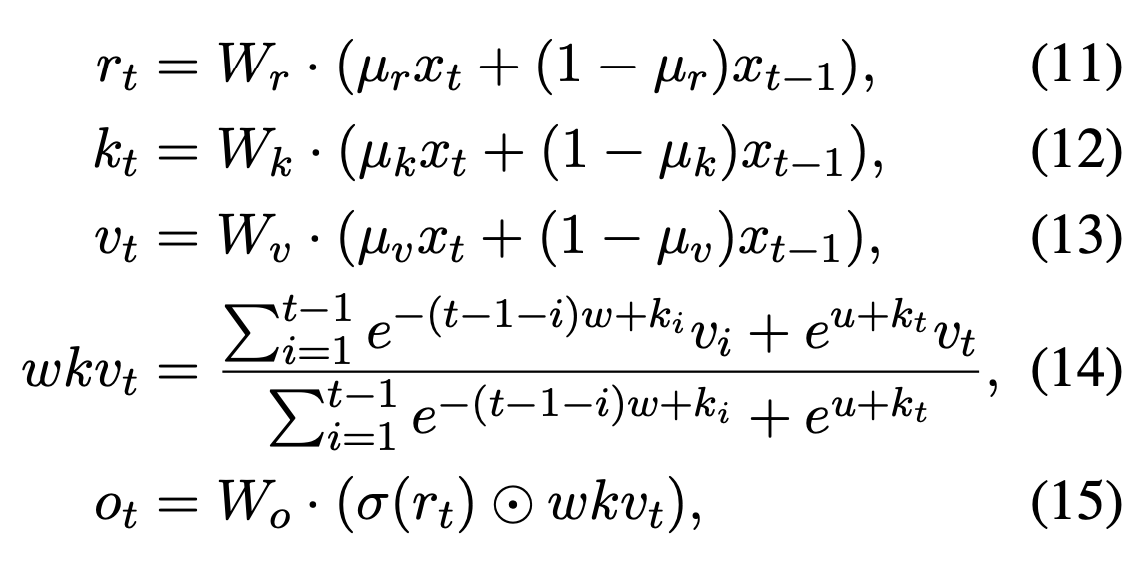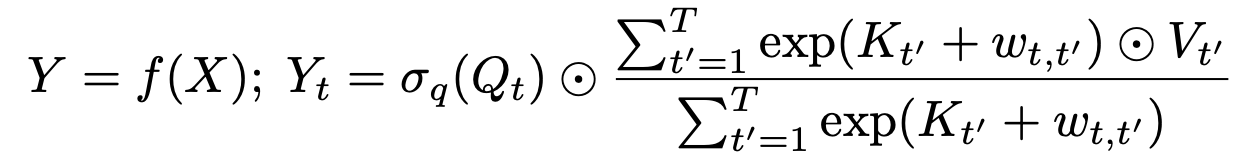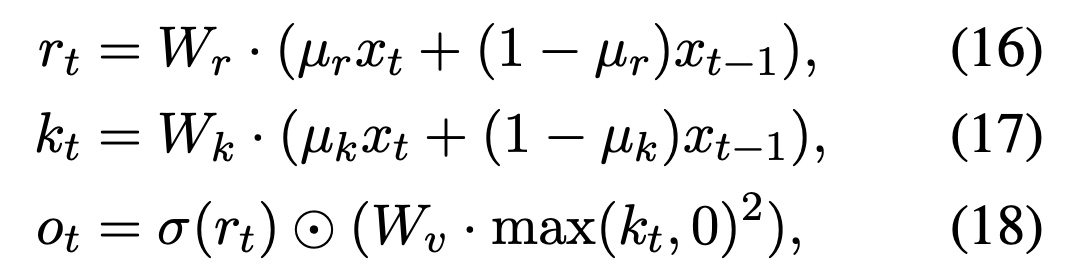RWKV: Reinventing RNNs for the Transformer Era
@PENG Bo 等人最新力作。
作为一个RNN,效果媲美Transformer,并且具有较低的复杂度。
39 个回答
更新:下面是非常旧的回答了。
目前最新的GUI,可以在Win Linux Mac运行:https://github.com/josStorer/RWKV-Runner/releases
目前新的模型:v5 world:BlinkDL/rwkv-5-world at main
和 v4 world:BlinkDL/rwkv-4-world at main
===========
!!!下面是非常旧的回答!!!
!!!下面是非常旧的回答!!!
!!!下面是非常旧的回答!!!
!!!下面是非常旧的回答!!!
!!!下面是非常旧的回答!!!
!!!下面是非常旧的回答!!!
感谢关注,下面是RWKV的在线体验网址(在线是单轮。多轮可以自己部署,效果也很好):
问答,英文14B Raven:ChatRWKV - a Hugging Face Space by BlinkDL
问答,英文7B Raven:Raven RWKV 7B - a Hugging Face Space by BlinkDL
问答,中文7B Raven:https://www.codewithgpu.com/i/app/BlinkDL/ChatRWKV/RWKV-4-Raven-7B
中文请用中文模型,英文请用英文模型。目前英文模型强很多,因为目前中文模型是从英文模型+少量中文语料微调的。
正在炼支持100种全球语言的World基底模型:BlinkDL/rwkv-4-world · Hugging Face(这个模型很强,例如现在发布的World 7B只炼了52%就很强)。
Instruction填命令或问题,Input填背景参考资料(如果没有就留空),不要填反了。
- 例如,用中文7B Raven模型做小说扩写,Instruction填“请扩写:林凡和龙傲天大战”之类。Input留空,或者填“关键词:XX,XX”之类(这个没训练过,但似乎有用)。
- 例如,做文本摘要,在Instruction填指令,在Input填需要摘要的文本。
解码参数非常重要。模型的原始状态是 topp 1,temp 1,penalty 0,此时它是一个“狂躁病患者”。
降低topp:给模型喂“镇静剂”,越低就越冷静、机械、准确、单调、无趣、重复:
- 创意回答和写作,建议topp 0.5~0.7。
- 机械的问答和摘要和翻译等等,建议topp 0~0.5,甚至 0~0.3。
- 很机械的回答,例如回答“是/否”、ABCD、1234之类,建议topp 0。
增加temp:给模型“喝酒”。它可以在topp低时,增加文采和趣味,减少重复:
- 若topp >= 0.7,建议temp 1。
- 若topp < 0.7,而且追求趣味,可以增加temp给模型喝酒(喝太多会胡言乱语)。如果追求准确,就保持temp 1。
- 如果topp 0.5,建议temp 1~1.5。
- 如果topp 0.3,建议temp 1~1.7。
- 如果topp <= 0.2,建议temp 1~2。
推荐的写小说设置:
- topp 0.5 temp 1.2 或 topp 0.4 temp 1.5 或 topp 0.3 temp 1.7 或 topp 0.2 temp 2。自己看喜欢哪种。
增加penalty:让模型额外避免生成已经生成过的字。建议先设为0.2~0.4。如果你认为生成的内容有重复,而且调topp和temp仍然不满意,可以调整penalty。注意,如果设置过高,会让模型无法使用正常字,例如无法使用正常标点,或者直接乱码。
- 如果topp 0.7,建议penalty 0~0.3。
- 如果topp 0.5,建议penalty 0~0.5。
- 如果topp 0.3,建议penalty 0~0.7。
- 如果topp <= 0.2,建议penalty 0~1。
RWKV微调教程:
英文14B的效果例子,输入公式(TeX),输出代码:
中文小说续写,均衡文风:ModelScope 魔搭社区
中文小说续写,小白文风:ModelScope 魔搭社区
中文小说续写,专业文风:ModelScope 魔搭社区
本地部署,懒人请用懒人包:
懒人包1(推荐):1466:RWKV-Runner发布并开源,可商用的大语言模型,一键启动管理,2-32G显存适配,API兼容,一切前端皆可用
懒人包2:ChatRWKV教程与工具
会动手的用户,用我写的 ChatRWKV,因为目前大多数第三方实现仍有 bug,例如 HF rwkv 仍有 bug。使用请设置正确 strategy,并编译 CUDA 算子,这对于运行速度极其重要。
教程:PENG Bo:发布几个RWKV的Chat模型(包括英文和中文)7B/14B欢迎大家玩
RWKV pip package:rwkv
请务必用最新和正确的模型。例如Raven是v某某,某某越大越新。注意语言比例需要正确,例如中文模型是Chn49%。
后续欢迎大家来玩的:
- 可解释性,可视化。由于RWKV作为RNN有明确的固定大小state,可以做许多transformer做不到的事情。例如,我们可以直接分析理解和操纵RWKV的状态,还可以直接做高效P-tuning。
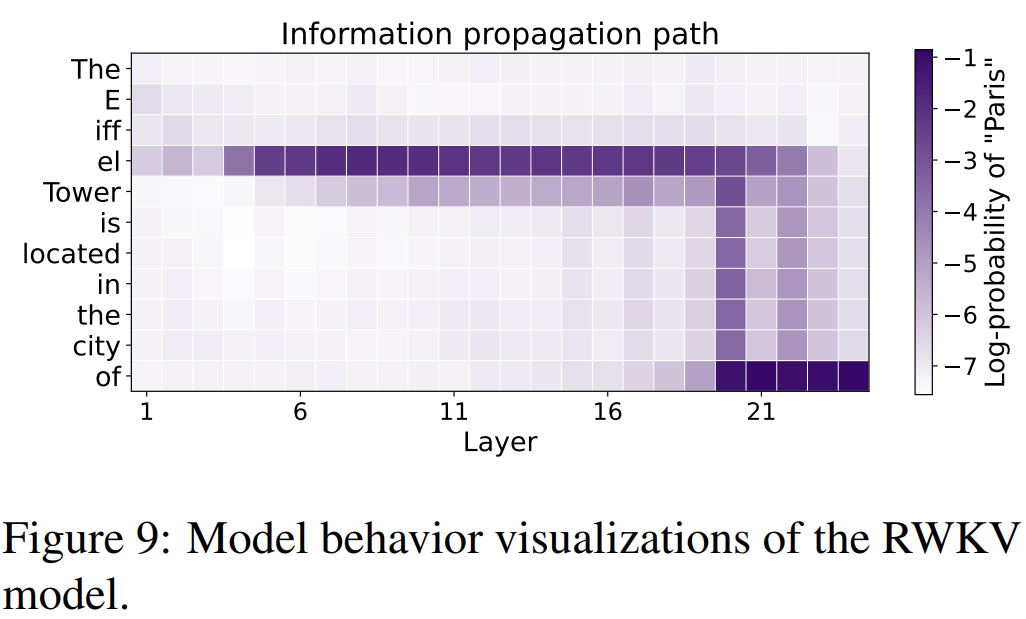
2. 多模态。state是优质的嵌入(注意区分 x a b p)。
3. 量化,稀疏,端侧高速运行。
4. 插件,向量数据库,检索增强,AutoGPT等等。
另外大家记得看论文附录,例如这些都在附录:
最后,我发现某些人真的 low 穿地心。刚才知乎推荐一条答案,竟然有人说我“为了寻求支持出让两个一作位置”。
我告诉你,是我告诉 EleutherAI ,我希望支持 EleutherAI 这个开源机构,所以我希望给他们多一些 credit,正如我将论文的写作开放给整个社区。
这个世界需要更多 Open AI 践行者,需要我们大家一起努力。
刚扫了下paper,写个简单的解读,如有错误/遗漏欢迎评论区指出~
首先,在模型高度同质化的今天敢于往不太流行的架构上砸资源而且训练到效果不错是值得respect的,值得关注后续scale up的潜力,甚至其余的efficient transformer架构scale up后的效果也值得重新探索一下。
前面之所以用了efficient transformer而不是宣传里的RNN是因为这个架构我觉得其实还是更偏向transformer一点,按照论文里给的内容简单溯源拆解一下:
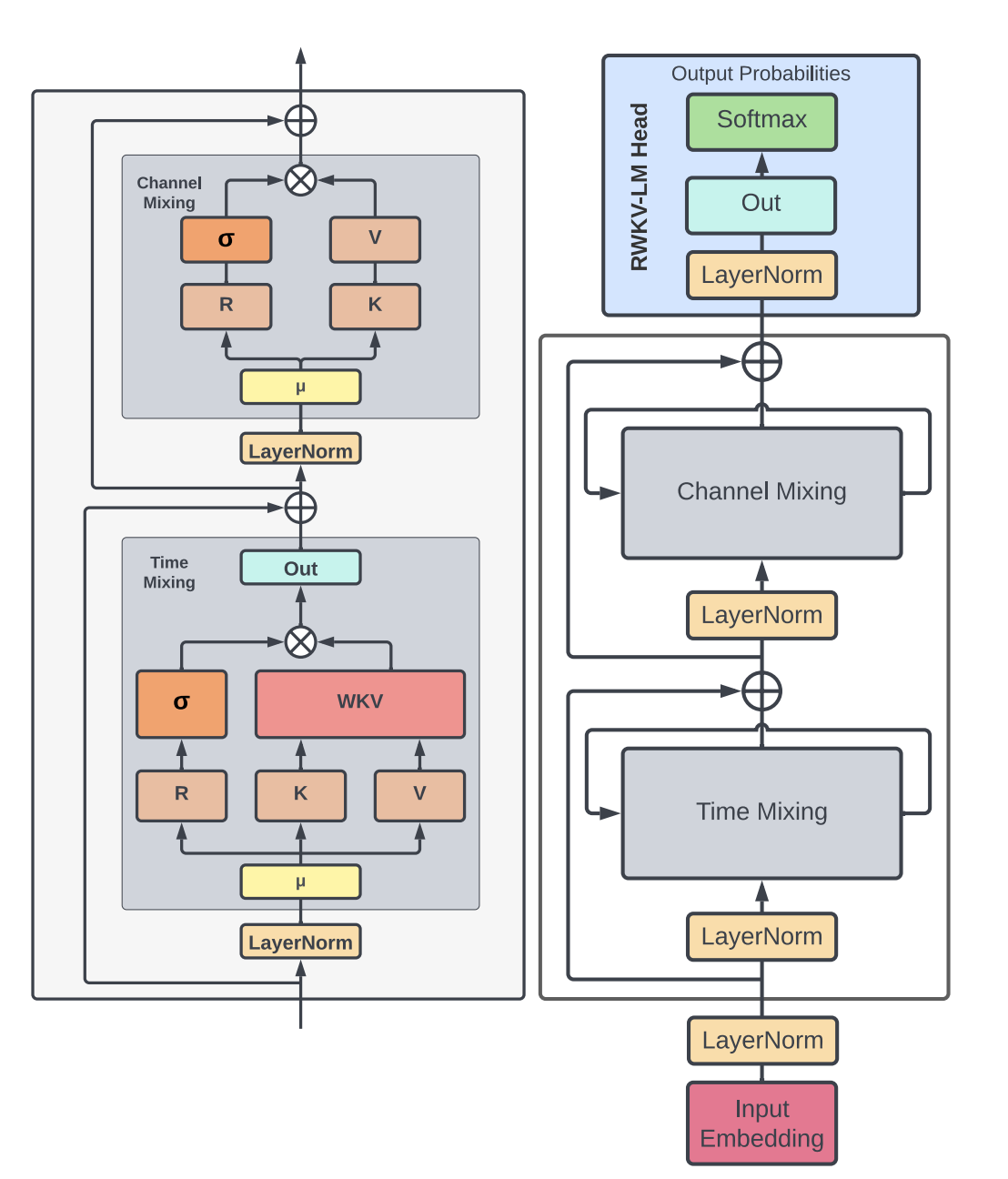
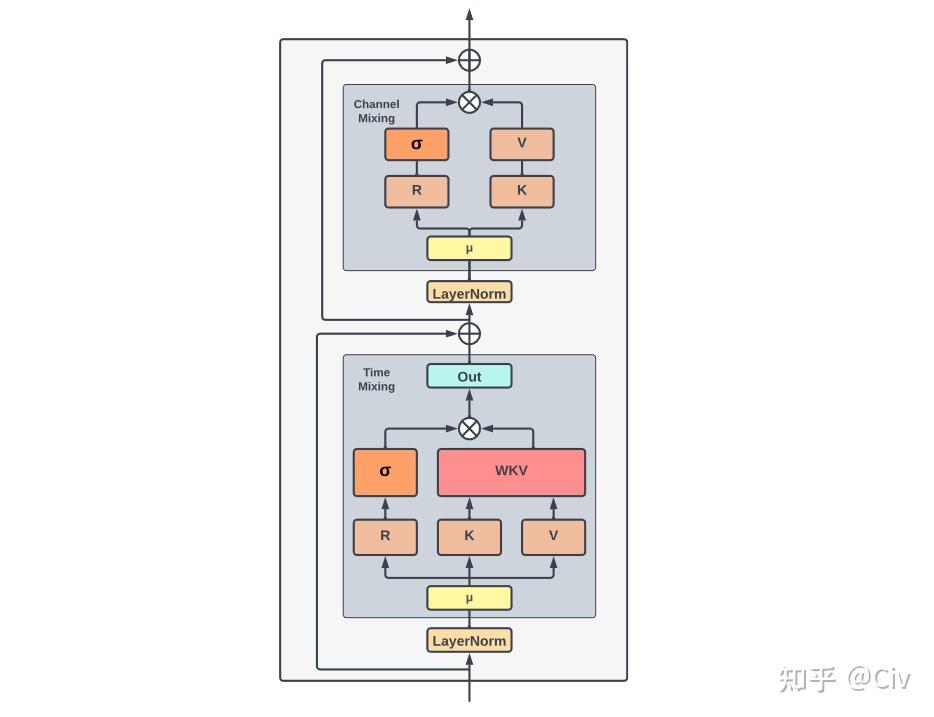
首先整体的架构上跟transformer一脉相承,每一层先做token间的mixing再做token-wise transformation,前两年比较火的MLP系列也是遵循这个思路。RWKV把对token间的mixing称为time mixing,从上图整体看下来就是linear attention的结构,先算KV再跟Q算结果:
\frac{\phi (q_i)\sum_j \phi (k_j) \odot v_j}{\phi (q_i)\sum_{j^\prime}\phi (k_{j^\prime})^T}
这样带来一个好处就是可以写成RNN的形式,非常适合自回归生成,比如上式的 \sum_j \phi (k_j) \odot v_j 和 \sum_{j^\prime}\phi (k_{j^\prime})^T 可以一直累加,避免了每一步都重新计算attention矩阵(具体的见https://arxiv.org/pdf/2006.16236.pdf)。往下翻,RWKV给出了具体的time mixing计算方式:
(11-13)就是attention里面的QKV projection,只不过投影前加了个窗口为2的卷积,(14-15)沿用了attention-free transformer的形式(https://arxiv.org/pdf/2105.14103.pdf),里面的相对位置编码w做了点调整。
接着是FFN部分,RWKV叫做channel mixing(沿用了MLP-Mixer的叫法),计算方式如下:
看起来还是先做一个窗口为2的卷积加一个非对称的GLU(https://arxiv.org/pdf/1612.08083v3.pdf),激活函数用了平方ReLU。
简单总结一下:
- 整体架构沿用了transformer及其后续MLP-Mixer系列的token-mixing & channel mixing结构
- token-mixing可以简单理解为kernel_size=2的卷积+AFT变体,channel mixing可以简单理解为kernel_size=2的卷积+GLU变体(当然任何模型结构上的简单修改最终训练起来并不简单,这里仅方便理解
- RNN主要体现在前面提到的linearized attention,使得可以写成适合自回归的RNN形式(前面大量出现的 \mu x_t+(1-\mu)x_{t-1} 更像是卷积,后面channel-mixing里面的结构可以理解是遗忘门,也可以理解是GLU,见仁见智,更重要的应该还是在于linearized attention
- 在具有速度和长文本优势下做到这个效果是很赞的,希望看到更多的ablation,比如这个kernel_size=2的卷积影响多大?平方ReLU相对于ReLU的影响多大?
抛砖引玉,欢迎作者来补充或纠错 @PENG Bo
1、写在前面,RWKV是一个不错的线性RNN模型;
2、RNN的优势是推理友好,线性RNN的优势还包括训练可并行,不过要注意的是RWKV的官方实现方式是CUDA实现的递归,也就是说RWKV并没有用到训练可并行这一点,所以单从训练速度来看,是不是线性的没太大区别(或者说模型足够大时,直接递归的并行效率已经足够了);
3、看得出RWKV的作者认真做了不少事情,但他(在国内)的PR文风显然会让不少人不喜甚至反感(也可能只是我的问题);
4、RWKV不能直接处理任意长序列,因为长度外推效果并不好,我猜测线性RNN的长度外推效果都可能欠佳,当然,长度外推问题在Attention中同样存在;
5、RNN是纯靠记忆来完成任务的,简单来说就是只会闭卷考试不会开卷考试(不会往前翻书),比如做阅读理解,如果先给材料再给问题,它是先把材料背下来,然后再回答问题,所以RWKV对prompt比较敏感,要把Task tokens放到最前面才比较好,也就是带着问题去阅读材料;
6、模型越大,RNN的优势会相对越不明显,因为模型越大,hidden_size也越大(远超出了要处理的序列长度),此时即便是Attention的效率也是近乎线性的,当然,我说的是相对不明显;如果是序列足够长呢?那么又回到第4、5点;
7、个人浅见,RNN、RWKV要进一步完善,就要想办法补上“翻书”能力,比较简单的方式就是补上若干层Attention,当然,这跟作者想要塑造的“RNN is all you need”的形象不符,但事实上,即便将RWKV套上NBCE来扩展Context长度,也相当于加入了一层Attention了。
刚关注RWKV不到两周,论文就出来了,挺奇妙。
理解RWKV的两个关键点是:
- Complexity
- Sequential Decoding
首先从Linear Transformer讲起,然后再介绍RWKV paper中反复提到的AFT,最后再看RWKV。
NOTE:为了大家方便比较几篇paper的公式,文本统一了三篇paper中的符号,所有公式重写了,所以和原文对比时请注意。
1. 理解Linear Transformer
论文链接:Transformers are rnns: Fast autoregressive transformers with linear attention
Linear Transformer解决的问题是将Transformer中self-attention的计算复杂度由 O(N^2) 降低为 O(N) ,其中 N 是序列长度。这对加快Transformer整体的training和inference过程非常重要。
沿用论文中的符号,把Linear Transformer的过程拆解一下。
用符号 x \in \mathbb R^{N \times F} 表示一个长度为 N ,特征维度为 F 的序列。 x 可以看作是self-attention模块的输入。Transformer中self-attention的典型计算如下:
(1) V' = softmax(\frac{QK^T}{\sqrt D}) V
其中矩阵Q、K、V是由输入 x 经线性变化得到的query、key、value。如果用下标 i 来表示矩阵的第 i 行(如 Q_i 表示矩阵 Q 的第 i 行),那么可以将公式(1)中的计算用如下形式抽象出来:
(2) V_i' = \frac{\sum_{j=1}^{N} \mathrm {sim} (Q_i, K_j) V_j}{\sum_{j=1}^{N} \mathrm {sim} (Q_i, K_j)}
其中sim() 为抽象出的计算Query和Key相似度的函数。在Transformer中,sim()定义为:
(3) \mathrm {sim} (Q_i, K_j) = \mathrm {exp} \left( \frac{Q_iK_j^T}{\sqrt D} \right)
在这种抽象下,可以将sim()定义为任何我们希望的形式。上述定义过程中对sim()唯一的约束是它需要非负。Linear Transformer采用了kernel来定义公式(3)中的sim:
(4) \mathrm {sim} (Q_i, K_j) = \phi(Q_i) \phi(K_j)^T
其中 \phi 是一个特征映射函数,可根据情况自行设计。Linear Transformer使用的 \phi 定义为:
(5) \phi (x) = \mathrm {elu} (x) + 1
将公式(4)代入公式(2)可得:
(6) V_i' = \frac{\sum_{j=1}^{N} \phi(Q_i) \phi(K_j)^T V_j}{\sum_{j=1}^{N} \phi(Q_i) \phi(K_j)^T}
注意上式中求和项与 i 无关,因此可以把与 i 有关的项提到前面,整理后可得:
(7) V_i' = \frac{\phi(Q_i) \sum_{j=1}^{N}\phi(K_j)^T V_j}{\phi(Q_i) \sum_{j=1}^{N}\phi(K_j)^T}
Transformer的计算复杂度随序列长度N呈二次方增长: O(N^2) 。可以用for循环来理解这个二次方:attention的计算包含两层for循环,外层是对于每一个Query,我们需要计算它对应token的新表征;内层for循环是为了计算每一个Query对应的新表征,需要让该Query与每一个Key进行计算。 所以外层是 for q in Queries,内层是 for k in Keys。Queries数量和Keys数量都是N,所以复杂度是 O(N^2) 。
再看Linear Transformer,它只有外层for q in Queries这个循环了。因为求和项的计算与 i 无关,所以所有的 Q_i 可以共享求和项的值。换言之,求和项的值可以只计算一次,然后存在内存中供所有 Q_i 去使用。所以Linear Transformer的计算复杂度是 O(N) 。
上述是Encoder,因为对于 Q_i ,没有限制它只能看左边(之前)的token。再来看Decoder,只需要把公式(2)中的N替换成当前token(第 i 个):
(8) V_i' = \frac{\sum_{j=1}^{i} \mathrm {sim} (Q_i, K_j) V_j}{\sum_{j=1}^{i} \mathrm {sim} (Q_i, K_j)}
再将Linear Transformer中定义的sim函数代入,可得:
(9) V_i' = \frac{\phi(Q_i) \sum_{j=1}^{i}\phi(K_j)^T V_j}{\phi(Q_i) \sum_{j=1}^{i}\phi(K_j)^T}
最后引入以下两个新符号:
(10) S_i = \sum_{j=1}^{i}\phi(K_j)^T V_j
(11) Z_i = \sum_{j=1}^{i}\phi(K_j)^T
稍作变换,可以将 S_i 和 Z_i 写作递归形式:
(12) S_i = \sum_{j=1}^{i}\phi(K_j)^T V_j = \phi(K_i)^T V_i + \sum_{j=1}^{i-1}\phi(K_j)^T V_j = \phi(K_i)^T V_i + S_{i -1}
(13) Z_i = \sum_{j=1}^{i}\phi(K_j)^T = \phi(K_i)^T + \sum_{j=1}^{i-1}\phi(K_j)^T= \phi(K_i)^T + Z_{i -1}
因此,在inference阶段,当需要计算第i+1时刻的输出时,Linear Transformer可以复用之前的状态 S_{i-1} 和 Z_{i-1} ,再额外加上一个与当前时刻相关的计算量即可。而Transformer在计算第i+1时刻的输出时,它在第i个时刻的所有计算都无法被i+1时刻所复用。因此,Linear Transformer更加高效。
总结一下:
- Linear Transformer的计算复杂度为 O(N) (不考虑embedding的维度的情况下)
- 如公式(12)和(13)所示,因为 S_i 可由 S_{i-1} 计算得到( Z_i 同理),所以它可实现Sequential Decoding(先算 S_1 ,由 S_1 算 S_2 ,以此类推)。
能Sequential Decoding是让这类Transformer看起来像RNN的核心原因。
2. 理解Attention Free Transformer (AFT)
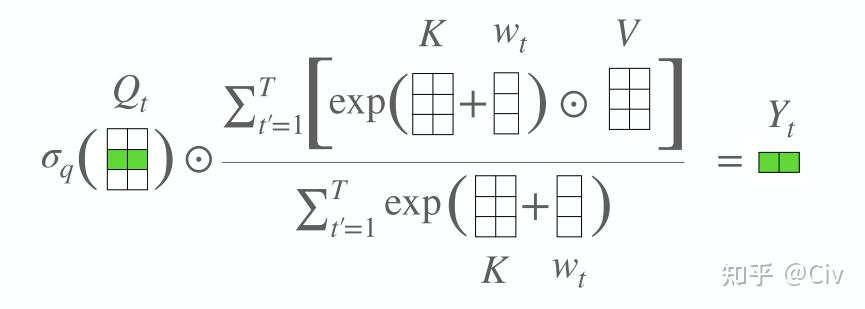
论文链接:Attention Free Transformer (AFT)
这里直接列出AFT的Decoder形式:
(14) V_i' = \sigma (Q_i) \odot \frac{\sum_{j=1}^i exp(K_j + w_{i,j}) \odot V_j}{\sum_{j=1}^i exp(K_j + w_{i,j})}
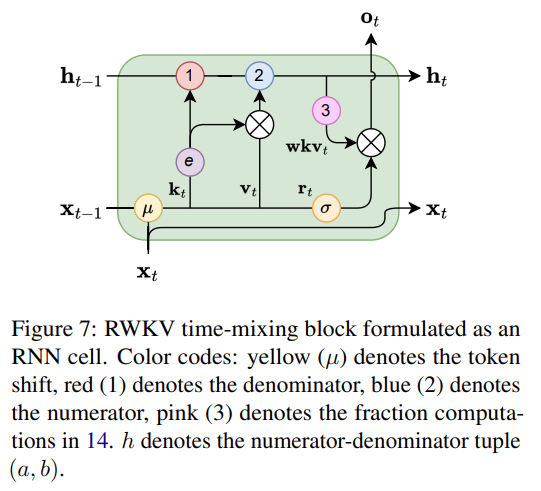
其中 \sigma 是sigmoid函数; \odot 是逐元素相乘(element-wise product); w_{i,j} 是待训练的参数。图1是示意图,其实画的并不算特别直观,要多看几次。核心是:1)按行计算;2)vector + scalar 等于vector中每个元素加scalar ;3)vector1除以vector2 等于逐元素相除。
AFT采用的形式和上面的Linear Transformer不一样。 首先是attention score,Linear Transformer仍然是同Transformer一样,为每一个Value赋予一个weight。而AFT会为每个dimension赋予weight。换言之,在Linear Transformer中,同一个Value中不同dimension的weight是一致的;而AFT同一Value中不同dimension的weight不同。
此外,attention score的计算也变得格外简单,用K去加一个可训练的bias(bias与位置pair对一 一对应)。Q的用法很像一个gate。
可以很容易仿照公式(12)和(13)把AFT也写成递归形式,这样容易看出,AFT也可以像Linear Transformer,在inference阶段复用前面时刻的计算结果,从而相比于Transformer变得更加高效。
总结一下:
- AFT的计算复杂度为 O(N^2) ,与Transformer一样。这是因为公式(14)的求和项中与 i 相关。
- AFT可以实现Sequential Decoding,因为公式(14)也可以写成递归形式。
3. RWKV
RWKV的目的是:
- 改造AFT,让其复杂度为 O(N)
- 保留AFT简单的“attention”形式
- 保留AFT的Sequential Decoding
对着paper中的这张图看即可:
首先看time-mixing block。time-mixing的目的是“global interaction”,对应于Transformer中的self-attention。其中使用到的R、K、V对应于AFT(或Transformer)中的Q、K、V。也就是说,K、V的含义可以强行看作一致,把R当做Q来处理就行。
只是RKV的计算方法有点变化:
(15) R_i = W_r \cdot (\mu_r x_t + (1- \mu_r) x_{t-1})
(16) K_i = W_k \cdot (\mu_k x_t + (1- \mu_k) x_{t-1})
(17) V_i = W_v \cdot (\mu_v x_t + (1- \mu_v) x_{t-1})
R、K、V的计算和Transformer的区别是,作为计算RKV(QKV)的输入的x不再是当前token的embedding,而是当前token与上一个token embedding的加权和。
然后是最重要的"attention"用了如下方法计算:
(18) V_i'=\frac{\sum_{j=1}^{i-1}e^{ -(i-1-j)w+K_j} \odot V_j + e^{u+K_i}\odot V_i} {\sum_{j=1}^{i-1}e^{ -(i-1-j)w+K_j} + e^{u+K_i}}
需要拿着这个公式和AFT的公式(14)去仔细对比。容易发现,改动是两点:
- 原来的依靠绝对位置的bias w_{i,j} 没有了,改成了相对位置,并且只有一个参数 w 向量需要训练。
- 对当前位置单独处理,增加了参数 u 。
公式(18)应该是经过比较精密地设计才弄出来的。它最大的特点是,也可以写成递归形式(参照原文公式19-22,不搬运了),这就让RWKV兼顾了Linear Transformer的 O(N) 以及AFT的简洁。
time-mixing block的最终输出:
(19) O_i=W_0 \cdot (\sigma(R_i) \odot V_i')
channel-mixing block根据time-mixing block的输出重新使用公式(16)、(17)去计算了一组新的R和K。然后再计算最终输出如下:
(20) O_i= \sigma(R_i) \odot (W_v \cdot max(K_i, 0)^2)
RWKV的核心就到这,其它内容都是在讲故事:一个关于RNN的故事。
4. 如何评价RWKV
回到正题。
评价一:凡是能让idea work起来的工作,都值得尊敬和钦佩。深度学习中,只要是以马后炮的心态来看待别人工作,都会觉得简单。所以talk is cheap,但作者们做到了show us the code.
评价二:从知道RWKV到看相关paper,时间太短,我比较好奇公式(18)是怎么设计出来的。这个公式有点丑,有没有可能让它稍微优雅点......
评价三:第一次看到RWKV的文章,下面一个评论说,叫“KTV”更容易记住。讲真,如果叫KTV,明天微博、朋友圈都会被连Transformer还没搞明白的人占领。值得考虑......
评价四:希望大家多支持一下这类工作,不易,不易,不易。
评价五:最近会尝试在手机上跑一下,有结果了给大家分享。