概要

この記事はデータ構造とアルゴリズム Advent Calendar 2019 の11日目の記事です。

この記事では、 $10^{100}$ 以下の全ての高度合成数を $1$ 秒以下で列挙する $2$ 種類のアルゴリズムおよびpythonコードを紹介します。計算時間は google colab (2019/12/02) で計測しました。

参考文献

高度合成数に関するlotzさんの素晴らしい記事があります。列挙アルゴリズムも複数紹介されています。
以下で紹介するアルゴリズムのうち、アルゴリズム1についてはlotzさんの記事およびinamoriさんの記事1 記事2 記事3　を参考にしています（本記事では枝刈り関数の変更などでさらなる高速化を達成しています）。
アルゴリズム2はdario2994さんのコード(gist)を読み解いて解説したものです。

高度合成数の定義

自然数で、それ未満のどの自然数よりも約数の個数が多いものを高度合成数といいます。
たとえば、以下の表を眺めると、 $1, 2, 4, 6, 12$ は高度合成数であることがわかります。

自然数	1	2	3	4	5	6	7	8	9	10	11	12
約数の個数	1	2	2	3	2	4	2	4	3	4	2	6

競技プログラミングでの使われ方の例

たとえば $10^{9}$ 以下の最大の高度合成数は $735134400$ であり、その約数の個数は $1344$ 個です。
よって、 $N$ の約数の個数の $2$ 乗オーダーで解けるような問題は、 $N \leq 10^{9}$ の制約のもとで $2$ 秒以内に計算が収まる可能性が高いです。

解きたい問題

$N$ 以下の高度合成数をすべて列挙せよ。ただし $N \leq 10^{100} .$

#ナイーブなアルゴリズム

$N$ 以下の全ての自然数の約数の個数を求めれば、高度合成数を列挙することができます。 $τ (1), τ (2), τ (3), \dots$ と順番に約数の個数を計算すると大変ですが、「各 $i$ について、 $n$ が $i$ の倍数ならnumber_of_div[n] += 1」とすると調和級数により $O (N \log N)$ で計算できます。

このアルゴリズムではすべての $i \leq N$ について約数の個数を計算しているので、少なくとも $N$ に比例する計算量が必要です。計算量を劇的に減らすためには、適切な枝刈りが必要です。

考察

自然数 $n$ の素因数分解を $n = 2^{e_{1}} 3^{e_{2}} \dots p_{r}^{e_{r}}$ （ただし $p_{r}$ は $r$ 番目の素数）として、 $n$ の約数の個数を $τ (n)$ とすると、
$τ (n) = (e_{1} + 1) \times \dots \times (e_{r} + 1)$
が成り立ちます。よって、自然数 $n$ の素因数分解から約数の個数を計算することができます。
なので自然数 $n$ だけでなく、その指数表記 $[e_{1}, \dots, e_{r}]$ も一緒に考えるとよいです。
たとえば、 $20 = 2^{2} \times 5 = [2, 0, 1]$ といった感じです。
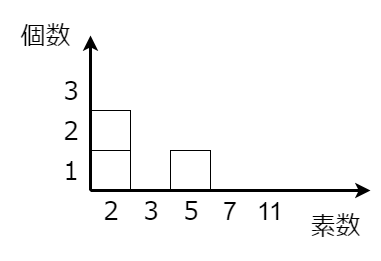
さらに、以下のように指数表記を図で表します。タイル表記としておきましょう。

以下の例は $20 = 2^{2} \times 5 = [2, 0, 1]$ のタイル表記です。
$20$ は $2$ で $2$ 回割り切れるので、 $1$ 列目にはタイルを縦に $2$ 枚並べます。
$20$ は $3$ で割り切れないので、 $2$ 列目にはタイルを並べません。
$20$ は $5$ で $1$ 回割り切れるので、 $3$ 列目にはタイルを縦に $1$ 枚並べます。
$20$ は $7$ 以上の素数で割り切れないので、 $4$ 列目以降にはタイルを並べません。

重要な枝刈り

指数表記と約数の個数に対応がついたので、枝刈りができるようになります。
たとえば、 $2^{2} \cdot 7$ は高度合成数になりません。なぜなら、 $2^{2} \cdot 3$ のほうが小さく、かつ約数の個数が等しいからです。一般化すると $n = [e_{1}, \dots, e_{r}]$ が高度合成数であるためには、 $e_{1} \geq \dots \geq e_{r}$ が必要条件だとわかります。

アルゴリズム1: 枝刈り最良優先探索

高度合成数の列挙に有効な、heapq（優先度つきキュー）を使う最良優先探索を以下に示します。

heapq には、 $(n, τ (n), n の指数表記)$ という tuple が入っている。
以下を繰り返す。
- heapq から最小元 $n$ を取り出す
- $n$ の約数の個数を見て、高度合成数の条件をみたすか調べる。みたしていたら保存する。
- $n$ の「近傍」の各元 $c$ について、 $c$ が「枝刈り条件」をみたすなら heapqに入れる

ここで大事なのは近傍の取り方です。次の性質をみたす近傍がとれるとよいです。

近傍の元のほうがもとの元よりも大きい
すべての元がちょうど1回ずつheapqに入るようにする
（上の2つの条件でアルゴリズムが正しい解を返すことが保証される）
加えてよい枝刈りができるなら、探索空間をグッと小さくすることができます。

ここでは、横積みと縦積みという、2種類の近傍の取り方を考えます。（下の図を参照）
両方とも、 $e_{1} \geq \dots \geq e_{r}$ という枝刈り条件のもとで上記の条件をみたします。

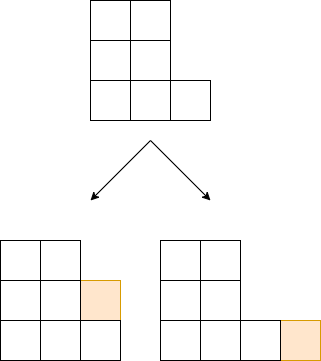
1-1 縦積み

縦積みでの近傍は上のタイル表記のように、右端の列を縦に伸ばす or 横に新しい列を増やすです。
つまり $[e_{1}, \dots, e_{r}]$ の近傍は $[e_{1}, \dots, e_{r} + 1]$ と $[e_{1}, \dots, e_{r}, 1]$ のふたつです。今回は $e_{1} \geq \dots \geq e_{n}$ という必要条件があるので、一つめの近傍は $e_{r - 1} > e_{r}$ のときだけ考慮すれば大丈夫です。
（逆にこの必要条件がない場合、 $[e_{1}, \dots, e_{r - 1}, 1]$ の近傍として $[e_{1}, \dots, e_{r - 1}, 0, 1]$ も追加すれば全自然数が探索できます）

このアルゴリズムでは、 $N = 10^{25}$ 程度までなら $2$ 秒以内に計算できます。
なお、縦積みの場合も横積みの場合（次節参照）と同様にさらなる枝刈りができますが、1割程度しか高速化できなかったので詳細は割愛します。

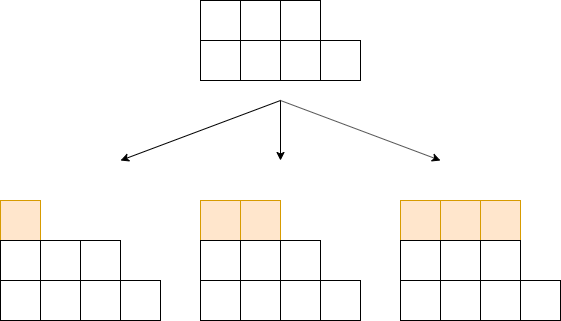
1-2 横積み

横積みでは、 $e_{1} \geq \dots \geq e_{r}$ をみたす元を全探索できます。
横積みの場合、近傍は上図のように、上に行を増やします。
つまり、 $[e_{1}, \dots, e_{r}]$ が与えられたとき、 $e_{1} = e_{j}$ をみたす任意の $j$ に対して $[e_{1} + 1, \dots, e_{j} + 1, e_{j + 1}, \dots, e_{r}]$ はその近傍です。
ただし、 $n$ の指数表記が全て $1$ のときだけ横に伸ばせるとします。たとえば $[1, 1, 1]$ の近傍は $[1, 1, 1, 1]$ も含みます。

枝刈りをしない場合でも、横積みは縦積みよりも効率的です。
なぜなら、横積みでの近傍になる自然数のほうが縦積みでの近傍になる自然数よりも小さいからです。
今回の問題では縦積みより $2$ 倍弱高速なコードとなり、 $N = 10^{30}$ くらいまでなら $2$ 秒以内に計算できるようです。

さらなる枝刈り

$x > y$ かつ $τ (x) \leq τ (y)$ のとき、 $x$ が負ける、 $y$ が勝つ、右が勝つと表現します。
枝刈りをするためには、「元 $x$ から近傍をたどっていける任意の元は高度合成数にならない」という $x$ を発見する必要があります。そのために以下の性質を確認しておきましょう（証明略）。

とある数に負けた数は絶対に高度合成数にはならない
$x$ vs $y$ で $y$ が勝つなら、 $x$ とも $y$ とも互いに素な数 $z$ について $x z$ vs $y z$ で $y z$ が勝つ
$x$ vs $y$ で $y$ が勝ち、素数 $p$ で割り切れる回数が $y$ より $x$ のほうが多いなら、 $x p$ vs $y p$ で $y p$ が勝つ

ここから次の枝刈り定理が導けます。

枝刈り定理

$p < q$ をともに素数とし、 $p^{e}$ vs $p^{e - x} q$ で右が勝つような $x$ があると仮定する。
このとき $q$ 以上の素因数を使わず、 $p$ で $e$ 回以上割り切れる任意の数は高度合成数でない。
とくに横積みの場合、そのような数はすべて枝刈りできる（つまりそのような数から近傍をたどっていける任意の数は高度合成数でない）。

枝刈りできる条件

では $p^{e}$ vs $p^{e - x} q$ で右が勝つ条件を整理しましょう。大小の条件より $x > \log q / \log p$ 、約数の条件より $x \leq (e + 1) / 2$ となるので、右が勝つ必要十分条件は $\log_{p} q \leq x \leq (e + 1) / 2$ なる整数 $x$ が存在することです。これの同値条件として
$2 (⌊ \log_{p} q ⌋ + 1) \leq e + 1$
がわかります。これなら左辺を前計算できるので、判定も $O (1)$ でできます。

この枝刈りの効果は劇的で、 $N = 10^{100}$ としても全ての高度合成数を $1$ 秒以下で列挙することができました。サンプルコードを以下に示します。

def hcn_heapq(N): #N以下の高度合成数を列挙したリストを返す
    from heapq import heappop,heappush
    from math import log
    prime = [2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,173,179,181,191,193,197,199,211,223,227,229,233,239,241,251,257,263]
    lim = [[2*int(log(p,q)) for q in prime] for p in prime] #枝刈り用配列
    # 初期状態
    q = [(2,2,[1])] # (n,nの約数の個数、nの指数表記)を保存する heapq
    res = [(1,1,[])]

    while q and q[0][0] <= N:
        n,val,lst = heappop(q)
        if val > res[-1][1]: #条件をみたすなら答に追加
            res.append((n,val,lst[:]))
        L = len(lst)
        e0 = lst[0]
        #全部１なら新しい素数で横に伸ばせる
        if e0 == 1: 
            heappush(q,(n*prime[L],val*2,[1]*(L+1)))
        #最上段の上を横方向に積む
        for i in range(L):
            if e0 > lst[i]: break #段差があると、もう伸ばせない
            if e0 >= lim[L][i]: break #枝刈り（重要）
            n *= prime[i]
            if n <= N:
                lst[i] += 1
                val = val//(e0+1)*(e0+2)
                heappush(q,(n,val,lst[:]))
    return res

N = 10**100
res = hcn_heapq(N)
print(len(res)) #N以下の高度合成数の個数
print(res[-1]) #N以下の最大の高度合成数

アルゴリズム2: 素因数DP

上述の通り、このアルゴリズムはdario2994さんのコードを読み解いて解説したものです。本アルゴリズムも、 $10^{100}$ 以下の全ての高度合成数を $1$ 秒以下で列挙することができます。

この種の問題に対しては、「 $k$ 番目以下の素数まででの計算値」をもとに「 $k + 1$ 番目以下の素数まででの計算値」を求めるという動的計画法も有効です。
本問題では、集合 $P (k, N)$ , $H (k, N)$ を以下で定めます。

$P (k, N)$ を、 $k$ 番目以下の素数の積で表される $N$ 以下の自然数全体の集合とする。
$H (k, N) = {k \in P (k, N) ∣ τ (n) > τ (m) \forall m < n,, m \in P (k, N)}$ とする。

$H (k, N)$ の定義は一見高度合成数そのものに見えますが、定義中の $m, n$ は $P (k, N)$ の元ということに注意です。たとえば $P (1, 30) = H (1, 30) = {1, 2, 4, 8, 16}$ のようになります。

重要な性質として、 $k$ が十分大きいときには $H (k, N)$ と $N$ 以下の高度合成数の集合が一致します!
つまり、 $N$ 以下の高度合成数は集合 $H (k, N)$ に属し、逆に $x \in H (k, N)$ かつ $x < p_{1} \dots p_{k + 1}$ ならば $x$ は高度合成数です。
よって $N < p_{1} \dots p_{k + 1}$ となる $k$ をとれば、 $H (k, N)$ こそが $N$ 以下の高度合成数の集合となります。

あとは $H (k, N)$ から $H (k + 1, N)$ への遷移を考察すればOKです。
$x \notin H (k, N) ⟹ x p_{k + 1}^{e_{k + 1}} \notin H (k + 1, N)$
が証明できるので、対偶をとって
$H (k + 1, N) \subset {x p_{k + 1}^{e_{k + 1}} ∣ x \in H (k, N)}$
となります。上式右辺の集合は $H (k, N)$ から計算できます。この集合をソートし、条件をみたすものを抽出することで $H (k + 1, N)$ が計算できます。

その他のアルゴリズム

「ちょうど $k$ 個」の素因数をもつ整数の集合 ${HCP}_{k}$ から高度合成数を列挙する手法があるようです。
https://shreevatsa.github.io/site/assets/hcn/hcn-algorithm.pdf
lotzさんの記事で言及されており、Haskellでの実装があります。きちんとした比較はしていませんが、パフォーマンスの面では本記事で紹介したアルゴリズムで十分という感触があります。

まとめ

本記事では高度合成数を高速に列挙する $2$ 種類のアルゴリズム、「枝刈り最良優先探索（横積み）」と「素因数DP」を紹介しました。計算量の解析はしていませんが、 $10^{100}$ 以下の全ての高度合成数を $1$ 秒以下で列挙することができます。
ちなみに $10^{100}$ 以下で最大の高度合成数は $9326516884061827509233332641260520263537022401378881409790204489294728443343865526159430547438720000$ で、約数の個数は $128581012920729600$ 個です。

Qiitaにログインしてダークテーマを使ってみませんか？🌙

高度合成数を高速に列挙する2つのアルゴリズム

概要