きっかけ

電場(電界)の数値解析について研究しているが、授業など真面目に聞かず遊んでばかりいたため、基礎知識が不足していると感じた。
電場計算の基礎的な知識を得るために、『数値電界計算の基礎と応用』という本を買った。
普通、電磁気系の数値解析の本といえば、電場計算、磁場計算、電磁波計算などが合わせて一つの本となっているのだが、この本は電場計算のみに特化した素晴らしい本である。

ただ、買っても読まないと意味ないので今回自分用のアウトプットのためにも、学んだことをここに書き留めたいと思う。
また、この本には数式の記述や、理論的な話はあっても、サンプルプログラムなどはない。
ただ書いていることを自分なりに解釈して記事にするだけでは面白くないので、pythonで自分で簡単にサンプルプログラムを実装していく。

なお、上記の本は電界と称されているが、本記事では電場に統一する。

電磁気学の理論・公式

当然だが電磁気学の理論をある程度知っていなければ、電界計算をできるわけない。
といっても、今回主眼に置くのは数値解析の方のため、超簡単に、必要なものだけ話していく。

今更だが、数学的な知識レベルとしては大学一年生～二年生レベルで話していこうと思う。
といっても、 $\nabla$ の記号やテイラー展開、あとは行列をなんとなく知っていれば多分大丈夫だ。

物理的な話なんてどうでもいい！って人はポアソン方程式まで飛ばして欲しい。

クーロンの法則

電磁気学の教科書で最初に出てくるのはたいていクーロンの法則だ。
高校の教科書では次のように書かれていると思う。

\begin{matrix} (1) & F = k \frac{q_{1} q_{2}}{r^{2}} \end{matrix}

ご存知の通り、

F

は力、

q 1

q 2

は２つの粒子の電荷、そして

r

は距離である。

(高校でも習うと思うが)大学になると、この比例定数 $k$ は真空の誘電率 $ε_{0}$ を利用して $k = 1 / (4 π ε_{0})$ と表現するのが普通になる。
さらに、ベクトル演算に慣れてくると、力 $F$ に方向の意味を持たせるためにも、次のように両辺ともベクトルで書くのが簡潔だ。

念の為行っておくが、ボールド体はベクトルを意味している。

\begin{aligned} F & = \frac{1}{4 π ε_{0}} \frac{q_{1} q_{2}}{| r |^{2}} \hat{r} \\ (2) & = \frac{1}{4 π ε_{0}} \frac{q_{1} q_{2}}{| r |^{3}} r \end{aligned}

$r$ は２つの粒子を結ぶベクトルで、 $\hat{r}$ は $r$ と同じ向きで、長さ $1$ のベクトルである。

一つ目は式(1)にただ２つの粒子を結ぶベクトルを加えただけで、最初はこっちのほうが見やすいと思う。
二つ目は $\hat{r}$ を、 $\hat{r} = r / | r |$ と置き直しただけである。
個人的には、こっちのほうが文字の種類が少なくなって好きだ。プログラム的にもこっちのほうが実装しやすそう。
今後もこっちの書き方で書いていくと思う。

上記の話は現実世界と同じ三次元の話であり、二次元だと少し違う。
どうしてこうなるか、という話はせず、公式だけ上げておこう。

F = \frac{1}{2 π ε_{0}} \frac{q_{1} q_{2}}{| r |^{2}} r

重要なのは、 $2 π$ になっているところ、そして分母の乗数が一つ減っているところだ。
球の表面積が $4 π$ なのに対して円の周の長さが $2 π$ であること、三次元から二次元に次元が一つ減ったことからなんとなくわかってほしい。

電場と電束密度

クーロンの法則は２つの電荷間に働く力の関係を表す式である。
このことから、電荷を１つ置くことで、この世界に何らかの場ができて、もう１つの電荷を置いたときにその場によって力が働くと考えることができる。
……何言っているかわからないかもしれないので、式をを利用して説明する。

クーロンの法則を $F = q_{2} E$ のように書き直したとき、

E = \frac{1}{4 π ε_{0}} \frac{r}{| r |^{3}} q_{1}

が電荷

q_{1}

が作る電場

E

である。

二次元のときは、クーロンの法則と同様に次のように表わされることも一応書いておこう。

E = \frac{1}{2 π ε_{0}} \frac{r}{| r |^{2}} q_{1}

ちょっと話が飛躍するが、微小領域での電荷 $q$ の値、電荷密度 $ρ$ を利用してうまいこと変形すると次式が得られる。
(この式の導出、当初はもう少し詳しく書こうと思ったのだが、いろいろな前提知識を説明しなければならないため省く。気になる人は自分で調べてみてね)

\nabla \cdot E = \frac{ρ}{ε_{0}}

なお、二次元のときも上式は変わらない。

ところで、電束密度 $D$ というものがある。
この電束密度 $D$ と電場 $E$ は、真空中では真空の誘電率 $ε_{0}$ を利用して、次のような比例関係が得られる。

D = ε_{0} E

とても簡単な式だが、この

D

と

E

の定義の物理的な意味は全く違うことには注意しよう。
電束密度は電荷が作る電気力線の密度、電場は電荷に力を及ぼす場である。

ポアソン方程式

電位 $ϕ$ は、次のように定義される。

\begin{matrix} (3) & - \nabla ϕ = E \end{matrix}

この式は、電場

E

という3次元ベクトルを1つのスカラー値に直すとても便利な式である。
このような値をスカラーポテンシャルと言う。

$\nabla \cdot E = ρ / ε_{0}$ に上式を代入すると、次式を求めることができる。

\nabla \cdot \nabla ϕ = - \frac{ρ}{ε_{0}}

この式を解けば、電位を求められるし、それを微分することで電場も求めることができる。

右辺の $ε_{0}$ などは定数なので、わざわざこれから書くのも面倒なので、もう少し一般的に書こう。
左辺を $u$ に、右辺を $f$ に置き直すと、次のように書き直すことができる。

\nabla \cdot \nabla u = f

このような式をポアソン方程式と呼ぶ。右辺のマイナスはとらないこともあるが、今回は書くのが面倒なので、とることにした。

長々と書いてきたが、結局、電場を求めるには、このポアソン方程式を解いて、電位を求めてから式(3)から電場を求めればOKだ。

境界条件(Boundary Condition, B.C.)

最後に、境界条件についてちょっとだけ話そう

無限遠点を電位の基準点とする(無限遠点での電位を0とする)と言う話はよく聞くと思う。
これは、境界条件を「無限遠点で0とする」として、上記のポアソン方程式を解く、と言う意味である。

数値解析では、ある計算領域内の値を求めるため、無限遠点を0と置くことは少ない(数値解析は無限遠点を境界条件とする問題は苦手であることが多い)。
そのため、境界条件の電位を基準値として解くことになる。

境界条件は主に以下の２つがある。

ディリクレ境界条件(第一境界条件)：計算領域の境界上において、 $u = g$ である。
ノイマン境界条件(第二境界条件)：計算領域の境界上において、 $\frac{\partial u}{\partial n} = g$ ( $n$ は境界の法線方向の微分)

上の $g$ は何らかの関数である。多分、定数のことが多いと思う。
他にも、周期境界条件やロビン条件(第三境界条件)などがあるが、今回説明は省く。

ポアソン方程式は、計算領域がディリクレあるいはノイマン境界条件で囲まれていれば解が存在することが証明されている。
注意すべき点として、ノイマン境界条件のみで囲まれている場合は基準値が指定されていないため、どこか任意の場所を基準値として指定する必要がある。

有限差分法(FDM)

ここまで来てついに数値解析の話に入っていく。長かった……。

上で述べたように、解くべき問題はポアソン方程式であり、計算領域はディリクレ／ノイマン境界条件に囲まれている。
これを、数式で表してまとめてみよう。

計算領域を $Ω$ 、その境界を $Γ$ としたとき、

\begin{aligned} \nabla \cdot \nabla u = f & (in Ω) \\ u = g_{1} (x, y) & (on Γ_{1}) \\ \frac{\partial u}{\partial n} = g_{2} (x, y) & (on Γ_{2}) \end{aligned}

ただし、 $Γ_{1} \cup Γ_{2} = Γ$ , $Γ_{1} \cap Γ_{2} = \emptyset$ である。

ちょっと抽象的な書き方なので、具体的な例で話す。
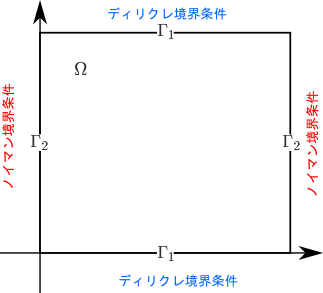
計算領域 $Ω$ を長方形とする。そして、境界 $Γ_{1}$ は上下の辺、 $Γ_{2}$ は左右の辺とすると、次の図のようになる。

図１：計算領域

ところで、 $Γ_{1} \cup Γ_{2} = Γ$ , $Γ_{1} \cap Γ_{2} = \emptyset$ の部分は流し読みせずちょっと立ち止まって考えて見てほしい。そんなに難しくないはずだ。
$Γ_{1}$ と $Γ_{2}$ の領域は被らず、その和集合が $Γ$ となるということも認識しておこう。わからない人はこちら「数式を読めるエンジニアになるために」(宣伝)。

このように、境界条件を与えられた偏微分問題を解くことを、境界値問題という。

この境界値問題を数値解析するに当たって、大抵最も最初に取り扱われあるのがこの有限差分法(Finite Difference Method: FDM) である。

なお、これ以降、二次元ポアソン方程式について考えていくことにする。
というのも、三次元だと図示するのが面倒だったりするからである。まあ、二次元さえわかれば三次元への拡張は容易だ。
即ち、次の偏微分方程式を解くことを考える。

\frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} = f

テイラー展開

まず、テイラー展開について話しておこう。
FDMはこれが全てであり、これさえわかれば極めたも同然だ。

一次元のテイラー展開

$Δ_{x}$ を極めて小さい値として、一次元のテイラー展開は次のように表される。

\begin{aligned} u (x + Δ_{x}) & = u (x) + Δ_{x} \frac{d u (x)}{d x} + \frac{Δ_{x}^{2}}{2!} \frac{d^{2} u (x)}{d x^{2}} + \frac{Δ_{x}^{3}}{3!} \frac{d^{3} u (x)}{d x^{3}} + \dots \\ = \sum_{p = 0}^{\infty} \frac{Δ_{x}^{p}}{p!} \frac{d^{p} u (x)}{d x^{p}} \end{aligned}

本当は、収束条件などがあるのが、今回は面倒なので無視しよう。

$Δ_{x}$ が小さい値なので、 $Δ_{x}^{3}$ 以降の項を無視してもまあ大体大丈夫だと考えよう。

u (x + Δ_{x}) \approx u (x) + Δ_{x} \frac{d u (x)}{d x} + \frac{Δ_{x}^{2}}{2!} \frac{d^{2} u (x)}{d x^{2}}

これは、

Δ_{x}^{3}

程度の誤差があると言うことで、次のように表記する。

\begin{matrix} (4) & u (x + Δ_{x}) = u (x) + Δ_{x} \frac{d u (x)}{d x} + \frac{Δ_{x}^{2}}{2!} \frac{d^{2} u (x)}{d x^{2}} + O (Δ_{x}^{3}) \end{matrix}

これを、

Δ^{3}

の誤差オーダーと言ったりもする。

また、同様に、次の式も得られる。

\begin{matrix} (5) & u (x - Δ_{x}) = u (x) - Δ_{x} \frac{d u (x)}{d x} + \frac{Δ_{x}^{2}}{2!} \frac{d^{2} u (x)}{d x^{2}} + O (Δ_{x}^{3}) \end{matrix}

式(4)と式(5)の二つを足すと、次のような式が得られる。

u (x + Δ_{x}) + u (x - Δ_{x}) = 2 u (x) + Δ_{x}^{2} \frac{d^{2} u (x)}{d x^{2}} + O (Δ_{x}^{4})

このとき、

Δ_{x}

の項と同様に、

Δ_{x}^{3}

のような奇数項全て打ち消してくれるため、誤差オーダーは

O (Δ_{x}^{4})

となる。

移行して整理すると、次の式が得られる。

\begin{matrix} (6) & \frac{d^{2} u (x)}{d x^{2}} = \frac{u (x + Δ_{x}) - 2 u (x) + u (x - Δ_{x})}{Δ_{x}^{2}} + O (Δ_{x}^{2}) \end{matrix}

即ち、

u

の二階微分は、右辺を計算することで(

Δ_{x}^{2}

オーダーの誤差を持つ値を)求めることができる。
このように

Δ_{x}^{2}

オーダーの誤差の精度を持つ(つまり、

Δ_{x}

を半分にすると、その二乗分誤差が小さくなる)ことを二次精度と言う。

二次元テイラー展開

一次元のテイラー展開は有名だが、多次元のテイラー展開は知らない人も多いかもしれない。
これは、次式で表される。

u (x + Δ_{x}, y + Δ_{y}) = \sum_{p = 0}^{\infty} \frac{1}{p!} {(Δ_{x} \frac{\partial}{\partial x} + Δ_{y} \frac{\partial}{\partial y})}^{p} u (x, y)

ただし、このとき、

{(\frac{\partial}{\partial x})}^{2} u = \frac{\partial^{2} u}{\partial x^{2}}

のように定義することにする。

例えば $Δ_{x} = Δ_{y} = Δ$ とすると、次のように展開できる。

\begin{matrix} u (x + Δ, y + Δ) = u (x, y) + Δ (\frac{\partial u (x, y)}{\partial x} + \frac{\partial u (x, y)}{\partial y}) \\ (7) & + \frac{Δ^{2}}{2} (\frac{\partial^{2} u (x, y)}{\partial x^{2}} + 2 \frac{\partial^{2} u (x, y)}{\partial x \partial y} + \frac{\partial^{2} u (x, y)}{\partial y^{2}}) + O (Δ^{3}) \end{matrix}

$x$ 方向または $y$ 方向にが一定の場合は一次元の式と同じになる。

\begin{aligned} u (x + Δ_{x}, y) = \sum_{p = 0}^{\infty} \frac{Δ_{x}^{p}}{p!} \frac{\partial^{p} u (x, y)}{\partial x^{p}} \\ (8) & u (x, y + Δ_{y}) = \sum_{p = 0}^{\infty} \frac{Δ_{y}^{p}}{p!} \frac{\partial^{p} u (x, y)}{\partial y^{p}} \end{aligned}

よし、準備はできた。
二次元ポアソン方程式のFDMを定式化していこう。

二次精度FDM

離散化

一応、もう一度ポアソン方程式をここに記す。

\frac{\partial^{2} u}{\partial x^{2}} + \frac{\partial^{2} u}{\partial y^{2}} = f

式(8)を利用すれば、一次元の二階微分を求めたときのように、次のような式が得られる。

\begin{aligned} \frac{\partial^{2} u (x + Δ_{x}, y)}{\partial x^{2}} = \frac{u (x + Δ_{x}, y) - 2 u (x, y) + u (x - Δ_{x}, y)}{Δ_{x}^{2}} + O (Δ_{x}^{2}) \\ \frac{\partial^{2} u (x, y + Δ_{y})}{\partial y^{2}} = \frac{u (x, y + Δ_{y}) - 2 u (x, y) + u (x, y - Δ_{y})}{Δ_{y}^{2}} + O (Δ_{y}^{2}) \end{aligned}

これをポアソン方程式に代入すると、次のような離散式が得られる。

\begin{matrix} \frac{u (x + Δ_{x}, y) - 2 u (x, y) + u (x - Δ_{x}, y)}{Δ_{x}^{2}} + \frac{u (x, y + Δ_{y}) - 2 u (x, y) + u (x, y - Δ_{y})}{Δ_{y}^{2}} \\ = f + O (Δ_{x, y}^{2}) \end{matrix}

ここで、 $O (Δ_{x, y}^{2}) = O (Δ_{x}^{2}) + O (Δ_{y}^{2})$ である。

ここまではなんとなく理解できただろうか。ちょっと式が多いが、言っていることはそんな難しくはないと思うので、ちょっと混乱したらもう一度読み直しておこう。

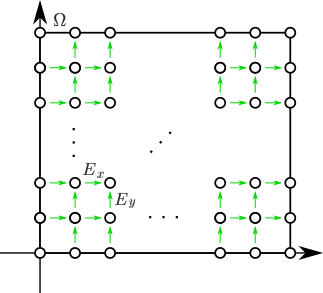
次に、次の図のように計算領域を格子分割する。

図２：格子分割

各格子点における $u$ の値を、 $u_{m, n} = u (m Δ_{x}, n Δ_{y})$ というように定義して、上の離散式に代入して整理すると、次のような式が得られる。

\frac{u_{m - 1, n} - 2 u_{m, n} + u_{m + 1, n}}{Δ_{x}^{2}} + \frac{u_{m, n - 1} - 2 u_{m, n} + u_{m, n + 1}}{Δ_{y}^{2}} = f_{m, n} + O (Δ_{x, y}^{2})

ここで

Δ_{x} = Δ_{y} = Δ

とすれば、次のように簡単になる。

\frac{u_{m - 1, n} + u_{m + 1, n} + u_{m, n - 1} + u_{m, n + 1} - 4 u_{m, n}}{Δ^{2}} = f_{m, n} + O (Δ^{2})

この $m$ , $n$ を整数とすれば、 $u_{m, n}$ を未知数とした連立方程式を立てることができることに気づける。
この連立方程式を解くことで、 $u$ の値を求めることができる。

説明のために、gif動画を作った。
以下のように、それぞれの点に注目して式を立てていく。

図３：定式化(思ったより大きくなってしまった……)

ここで、上式の未知数が12個( $u_{1, 0}, u_{2, 0}, u_{0, 1}, u_{1, 1}, u_{2, 1}, u_{3, 1}, u_{0, 2}, u_{1, 2}, u_{1, 3}, u_{2, 1}, u_{2, 2}$ )なのに対して、式はたった４つだ。これでは解けるわけがない。
ちょっと考えてみればわかるが、上のような2×2だけでなく、どんだけ大きくしても、式の数よりも未知数のほうが多くなってしまう。

そこで、境界条件の出番だ。

境界条件

図2のように計算領域をみると、境界上に格子点があることがわかる。
ここもいろいろなやり方があるが、このように格子点を置くのが最も簡単なのでこれで説明しよう。

ディリクレ境界条件

ディリクレ境界条件は次のように表されるのであった。

u = g_{1} (x, y) (on Γ_{1})

これはそのまま代入すればいい。

ノイマン境界条件

ノイマン境界条件は、一階偏微分だった。

\frac{\partial u}{\partial n} = g (on Γ_{1})

これも、(長方形領域の場合)とても簡単で、テイラー展開で一階微分の近似を行えばいい。
以下のような感じだ。

\begin{aligned} \frac{u_{m + 1, n} - u_{m, n}}{Δ_{x}} = g_{2} (x, y) \\ \frac{u_{m, n + 1} - u_{m, n}}{Δ_{y}} = g_{2} (x, y) \end{aligned}

なお、長方形領域のように、 $x$ 座標もしくは $y$ 座標と平行なら上式で簡単に求められるが、実際の計算領域は斜めになることが多い。この場合は、次回の実践編で説明する。

境界条件の右辺を $g_{1} (x, y) = 0$ , $g_{2} (x, y) = 0$ として、簡単な図を作ってみた。

図４：境界条件

領域の上下の辺をディリクレ境界条件、左右をノイマン境界条件にしたものである。

これによって、連立方程式の式の数=未知数の数となり、あとはその連立方程式を頑張って解くだけだ。

連立方程式

連立方程式の解き方は……、これはめちゃめちゃいろいろな手法があるのでここで説明はしない。
一応軽く触れておくと、連立方程式は行列を利用して次のように表すことができる。

A x = b

この

A

の逆行列

A^{- 1}

を求めて、

b

にかける直接法と、ガウス＝ザイデル法など何度も代入などを繰り返して解に近づけていく反復法がある。
直接法は時間がかかるが安定しており、反復法は発散する可能性があるが高速と、それぞれ一長一短がある。
ちなみにnumpyのnumpy.linalg.solveは直接法のLU分解という方法で解いている。

他の物理量への変換

最初に説明したように、ポアソン方程式から求まる解 $u$ は電位 $ϕ$ に値する。
この電位 $ϕ$ から電場 $E$ を求めるにはどうすればいいだろうか？

これも上のようにテイラー展開を利用しよう。
電位と電場は次のような関係があったのだった。

\nabla ϕ = E

x

成分は次のようになる。

\frac{\partial ϕ}{\partial x} = E_{x}

そして、テイラー展開による近似を行う。

\frac{ϕ_{m + 1, n} - ϕ_{m, n}}{Δ_{x}} = E_{x} (m Δ_{x}, n Δ_{y})

これは一次精度だが、求める電場を２つの格子点の中心とすれば、二次精度になる。

\frac{ϕ_{m + 1, n} - ϕ_{m, n}}{Δ_{x}} = E_{x} ((m + \frac{1}{2}) Δ_{x}, n Δ_{y})

図５：電場

上図のように、電場を求める際は格子点の間の値を求めるのが一般的である。

まとめ

電界解析はポアソン方程式さえ解ければいいということを説明した。

その解析方法として、今回は有限差分法(FDM)について説明した。
この有限差分法はテイラー展開に基づいており、これさえ理解できれば、あとは連立方程式を立てて、それを解けば解を求めることができる。

次回は、実践編と称して、この差分法を利用して実際にポアソン方程式を解くプログラムを作ってみよう。

電場の数値解析：有限差分法(FDM) －基礎編－