コンピュータグラフィックスにおいて、図形を変換するには、ベクトルやマトリックス(行列)の演算が多用されます。その中でも、Quaternion(= 4元数 = 虚数単位が3つある複素数)を用いて回転変換を表現する手法の数学的な解説をしたいと思います。通常の複素数の掛け算が、2次元複素平面での回転変換を表現できることの3次元への応用ともなっています。
補記:この記事は、Qiita でLaTeXを利用してみたい(参照:『Qiita 上で数式を美しく書けるようになっていた件 (MathJax)』)、というモチベーションで書いています。この記事『Java3Dの数学』の一部抜粋を読みやすくしたものです。また、コンピュータグラフィックスに慣れた読者には、最初の準備は長いと思いますので、後半のみ読んでください。
(準備1) 点とベクトル、それらの座標系を用いた表現
数学的な準備からはじめましょう。点もベクトル(有向線分)ももともとは図形、すなわち幾何的な実在であり、数とは直接関係していません。図形を数と関係付けるためには座標系を導入する必要があります。座標系を導入することで幾何を代数の言葉で表現できるようになります。すなわち、数式を使って図形を扱うことができるのです!これは数学者デカルトの功績であり、直交座標系はデカルト座標系とも呼ばれます。
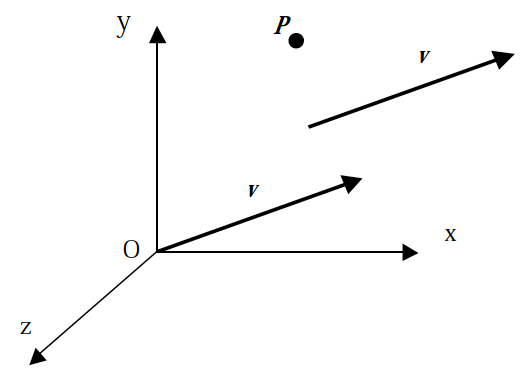
が座標系の原点です。ここでは座標系として右手系を使います。すなわちを中心に座標の+方向から座標の+方向へと右ねじを回したときにねじの進む方向が座標の+方向となるように規定します。あるいは,右手の親指と人差し指と中指を互いに直交するように伸ばしたとき, 軸がそれぞれ親指,人差し指,中指になるような配置とも言えます。図ではベクトル、は点を示しています。座標系を導入することで、点もベクトルも3つの実数の組で表現されます。ここではそれらの数学的記述として列ベクトルを用います。点およびベクトルは以下のように表されます.
メモ:点もベクトルも同じような表現になりますが、両者は区別して扱う必要があります。ベクトルは向きと大きさを持つ量であり、平行移動しても同じとみなされます(実際は「有向線分」を並行移動で"割った"ものです)。図でと記された2つのベクトルは同一視され、同じ値で表現されます。これに対して、点は平行移動すると別の点になり、別の値で表現されます。他にも違いがあります。2つの点の間には距離が定義できますが、2つのベクトルの間には距離が定義されません。その代わりベクトルには長さが定義されますが、点には長さが定義されません。さらに、ベクトル同士には足し算、引き算、およびスカラー(実数)倍の演算が規定されていますが、点同士は足し算ができませんし、スカラー倍も定義できません(これらの演算は座標系の取り方によって結果が変わってしまいます)。だだし,点同士の引き算はベクトルを生じ,点にベクトルを加えると新たな点が生成されます。
通常の教科書では、点は原点とその点を結ぶベクトル(位置ベクトル)として考えます。しかし、座標系を換えてしまうとその位置ベクトルは変化してしまうため、点の位置ベクトルは束縛ベクトルとも呼ばれます。(座標系に依らない、点とベクトルの代数系をご存知の方は教えてください。点ー点=ベクトル、点+ベクトル=点、のようなデカルト座標を持ち込まない系の代数です。。。)
(2020/10/11修正 まさに、 Weylの公理系 というのがそれに相当するようです。参考『線型代数学』佐竹一郎)
(準備2) マトリクスと変換
コンピュータグラフィックスでは、点およびベクトルの「変換」(他の点やベクトルに移動すること)は最も基本的な操作です。ここでは、変換とそれを表現するマトリクスについて説明します。
ベクトルと変換
まず、ベクトルの変換から考えてみます。前述のように座標家を考えると3次元空間のベクトルは3つの実数の組で表されます。ある変換を考え、ベクトルが変換によってに変換されたとします.これを,
と書き、簡単に、
とか、逆向きに、
と書きます。この変換が、仮に9つのパラメータ を使って,
と記述できるとき、この変換を「線形変換」といいます。ここで マトリクス を,
と定義すると、変換 は、
すなわち、
と書けます。 を を表現する変換マトリクスと呼びます。すべての変換が線形変換ではありません。すなわち、すべての変換がマトリクス で表現できるわけではありません。さまざまな変換の中でも、マトリクスの掛け算で表現できる変換を線形変換と呼ぶのです。(線形変換の性質、別の定義法については後述します。)
また、点の変換については点を位置ベクトルとして表現したものを変換すると考えると同じ結果になります。
回転変換
線形変換の例として、 軸回りの ラジアン回転変換は、
この場合の変換マトリックスは、 で表現され、
です。3次元空間上の任意の軸に関する回転はやや複雑なのでQuaternionとともに後述します.
スケール変換
回転と同様に、原点を中心としたスケール変換( 倍)に関する変換行列は、
となります。
線形変換の性質
これまで回転変換とスケール変換を例にして、線形変換を説明しました。ここでベクトルの線形変換の性質を改めて見てみましょう。ベクトルの線形変換には、名前からも明らかなように「線形性」があります。「線形性」とは,2つのベクトルの和を変換すると、個々のベクトルを変換した後に和をとったものと等しくなること、および、スカラー倍したベクトルを変換すると、もとのベクトルを変換した後にスカラー倍したものと等しくなることです。式で表すと,次のようになります。
最初の式が和に対する線形性、次の式がスカラー倍に対する線形成を表しています。 が線形変換の場合、 と書けることから上記の性質は自然に成り立つことがわかります。
最初、線形変換を「マトリクスで表現できること」と定義し、その性質として「線形性」を導きましたが、実は「線形性」そのものを線形変換の定義とし、そこから「マトリクスで表現できる」という性質を導くこともできます。
線形性に関する性質の中でも特にスカラー倍に関する性質から、「0ベクトルは0ベクトルに変換される」という大切な性質が導かれます。
点の平行移動と同次ベクトル
これまで回転変換とスケール変換を見てきました。これらはマトリクスで表現される線形変換です。次に、平行移動について考えてみます。べクトルに関しては平行移動は意味をなしません。平行移動してもベクトルの値は変化しないのですから。
点の平行移動は、点にベクトルを足すことで得られますが、これを変換マトリクスで表現することはできません。なぜでしょう?線形変換は0ベクトルを0ベクトルに変換するという性質がありますが,点を位置ベクトルとして捉えた場合,この性質は「原点は動かない」と読み替えることができます。平行移動は明らかにこの性質を満たしません。すなわち、点の並行移動は線形変換ではなく、そのままマトリクスの掛け算として扱うことはできないのです。
最初に述べたように、そもそも点という概念に対しては加算やスカラー倍が定義できないため、点の集合が代数でいう「線形空間」を形成してないことに問題があります。そこで、「3次元の点」を「4次元ベクトル」で表現するという工夫をします。これはコンピュータグラフィックスの数学で古くから行われている技法です。この4次元ベクトルを同次ベクトル(斉次ベクトル)と呼びます。4次元ベクトルを考え、4つ目の要素で残りの3つの要素を割り算したものを、3次元の点と同一視します。(※この図形的イメージについてどこかに書く)
通常は、 は常に 1 と考えておけば,4次元ベクトルの 座標がそのまま3次元の点の 座標と一致します.同次座標を導入することで,点の平行移動もマトリクスと列ベクトルとの積で表現できるようになります.すなわち,点を,ベクトル だけ平行移動した点を とすると
となるので、同次ベクトルを用いると、
あるいは、
ここで、
と書くことができます。
各変換まとめ
このように,4次元同次ベクトルと4次元マトリクスを用いることで,平行移動も、線形変換と同様にマトリクスの掛け算で扱うことができるようになります。これまで見た平行移動以外の回転、スケールの変換マトリクスはそのまま4次元に拡張できるので、回転、スケール、平行移動の3種類の変換はすべて 4x4 のマトリクスで表現できたことになります。
各変換は連続して行うことができます。たとえば、軸回りに回転した後、スケールして平行移動する変換マトリクス は、
という具合です.この場合,順に変換マトリクスを左から積算した結果できるマトリクスが合成変換のマトリクスとなります。
ちなみに 3 次元の点の4次元ベクトルへの拡張は,平行移動をも含めて点の変換をマトリクスの掛け算で扱おうという目的が主ですが、他にも とすることである方向の無限遠点を表現できたり、特定の場面で数値計算による誤差を押さえたり、さらに後述するように回転変換を表すQuaternionとの自然な演算が定義できるという数学的な利点もあります。
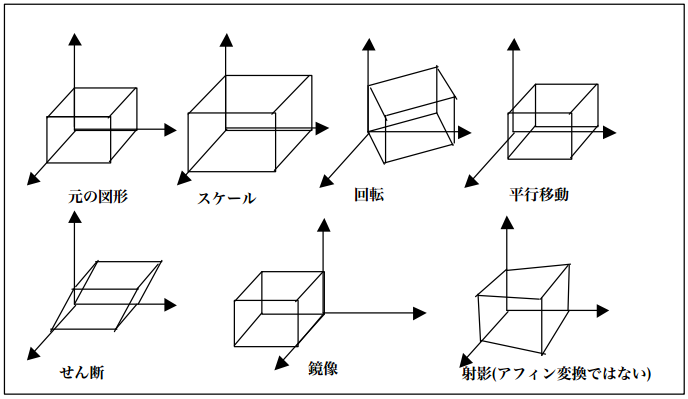
また、ここでは述べませんでしたが、他に、鏡像、せん断、と呼ばれる変換があります。鏡像は鏡に写した像を得る変換であり、せん断は斜めにつぶす変換です。せん断は、正方形を平行四辺形に変換します。回転、スケール、平行移動、鏡像、せん断から合成される変換をアフィン変換といいます。アフィン変換は,幾何的には「平行線を平行線に写す」という特徴で定義されます。
図中,射影変換はアフィン変換ではありませんが後述するので並べて掲載しています。中でも回転、スケール、平行移動の3つのアフィン変換は,図形の形を変えないためコンピュータグラフィックスで頻繁に用いられます。
アフィン変換を表現するの 4x4 のマトリクスは,
- 左上の 3x3 成分で,回転とスケールを表現
- 第4列(最も右の列)で平行移動を表現
- 第4行(最も下の行)はいつでも (0 0 0 1)
という特徴があります。次に、ようやく、先の回転変換と密接な関係をもつ Quaternion について説します。(ここまでが長い前置きです)
Quaternion
前節では、マトリクスによる回転の表現を見てきました。軸回りの回転のみを扱ったのは、任意の軸回りの回転はマトリクス表現では非常に複雑になってしまうからです。また、マトリクスによる表現はすべてのアフィン変換を扱うことができるため、変数の数が 4x4 = 16 (うち使うのは13)と多くなってしまいます.回転変換のみに焦点をあてたコンパクトな表現は他にないでしょうか?
回転の中心を原点と仮定すると、2次元ならば,回転角度だけで十分なのですが,3次元では任意の軸に関しての回転を表現する必要があるため、2次元ほど簡単ではないようです。
Quaternion は数学者ハミルトンによって導入された数です。クオータニオンと読み、日本語では4元数と訳されます(Quarter は4の意)。文字通り4つの要素を持つ数です。複素数の自然拡張になっており、3次元での回転変換を表現するのに便利であるため特にコンピュータグラフィックスで最近よく利用されます。
Quaternion は代数的に非常に美しい回転変換の表現です。美しいというのは,例えば Quaternion 同士の足し算や掛け算をも、意味をもって定義できるのです。また,マトリクスのようにアフィン変換すべてを表現しているわけではありません。3次元の回転変換の表現によくマッチした数であり,「スピナー(Spinner)」という回転を意味する別名を持っています。
結論だけ先に簡潔に述べると、単位ベクトル 回りの ラジアン回転を表す Quaternion は,
と表現されます。以下では、簡単に Quaternion を導入し回転変換との関係を解説しましょう。
定義
2つの実数の組で複素数を表現した時と同様に、4つの実数の組で Quaternion を表現します.まず,3つの単位虚数を導入することからはじめましょう。 は次の演算規則に従うものとします。
ここで、 の掛け算は非可換(交代)であることに注意してください。例えば、 = となります。
そして,4つの実数要素 を持つ Quaternion を以下のように定義します。
を実部、といい、を虚部といいます。
Quaternion の性質
Quaternion はベクトルと考えることで、和、スカラー倍が定義できますし、
虚数単位の演算規則を適用することでQuaternion同士の積も計算できます(計算は各自やってみてください)。
また、ある Quaternion に対して共役 Quaternion を、「実部のみもとの Quaternion と同じで虚部がもとの値のマイナスのもの」と定義します。
すると、Quaternion とその共役 Quaternion との積はスカラーになり、Quaternion のノルム(長さ)の2乗になります(虚部が0のQuaternionは実数と同一視します)。
逆 Quaternionを、「元のQuaternionと掛けたら1になるQuaternion」と定義します。
すると、共役Quaternionを使って、次のように求めることができます。
特に、ノルムが1の Quaternion を単位 Quaternion と呼びます,単位 Quaternion は3次元の回転変換と結びつく興味深い性質があります。
単位 Quaternion の性質
単位 Quaternion は次の性質をもつ Quaternion です。
通常の Quaternion を「単位化」するには、その長さで割ります。
以降、Quaternionは単位化されているとすると、次のような便利な性質があります。
さらに、長さが1であることから三角関数を使って、このように表現することができます。
これは、絶対値1の複素数の表現と非常によく似ていることがわかります。単位 Quaternion も, と を適当に選べば絶対値1の複素数と同じ形式で記述できます。数学に詳しい人なら、複素平面において絶対値1の複素数の掛け算が回転変換を表現することを思い出すでしょう。驚くべきことに、Quaternion においてもこの表記は、3次元空間でのを回転軸としたベクトルの回転を表現しているのです!
Quaternion と回転変換(ようやくハイライト)
では、点の回転を Quaternion で表現することを考えてみましょう。点の回転を Quaternion で回転を表現するためには、3次元の点と Quaternion の演算を定義しなければなりません。3次元の点 を4次元同次ベクトルで表し、それを Quaternion で表現しましょう。
そして先ほど定義した「積」の規則を使って,Quaternion に対応する の変換 を次のように定義します。
これで、点と Quaternion の演算が可能になります。実際に単位 Quaternion と点 について前の変換を計算してみましょう。
として、 と積の計算を行うと(ちょっとしんどいですが、机上で地道に計算します。実は「Java3Dの数学」ではこの式が間違っていたことが、今日判明しました。一項目の外積、 と が逆で、 でなく、 が正解でした。16年たって発見されました!!)、
となります。少し複雑に見えますが、ここから、
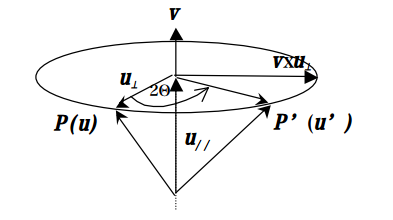
はベクトルを軸として点を 回転したものになっている
ことを示しましょう。 を と平行な成分 と v と直交する成分との2つのベクトルの和であると考えます。
ここで、 は次のように求められます。
はその定義から、次のような性質があります。
最後の式は難しいですが、に直行する単位ベクトル()を2回外積すると元にもどるベクトルの性質です。これらを使って計算を進めると、
というすっきりした式に置きかえることができます。計算途中で三角関数の2倍角の公式を使っています. は, との両方に直交し、と同じ長さのベクトルになります。この式を見ると、の 軸に平行成分はそのままにして,垂直成分のみを軸の回りに 回転させていることが分かるでしょう。
すなわち,単位ベクトル 回りの回転を表す Quaternion は, と置けば、
大円補完
Quaternion のもう1つの大きな特長は,2つのQuaternion の補間ができるということです.ある回転と別の回転との中間にあたる回転を求めたり,2つの回転の間を滑らかにつなぐ回転の計算を得意とします.一般の3次元の回転は,回転軸が固定されているならば角度のみの補間でかまいませんが,回転軸が変化する場合はマトリクスではうまい補間法がありません.回転をオイラー角のように x, y, z 軸の回転に分解する方法でも,分解方法が一意でないことから,補間は難しいとされています。ここでも、Quaternion が力を発揮します。
単位 Quaternion は,4次元空間の原点を中心とする半径1の球の表面にマップして考えることができます.すなわち,どんな単位 Quaternion でもその球面上の1点と考えることができるのです.これは,長さ1のQuaternion が を満たすことから容易に想像できるでしょう.Quaternion の補間では,球面上の2つのQuaternion を結ぶ大円(球面上の半径最大の円)を考え,その大円上で補間を行います.この大円補間は 以下のように定式化されます.
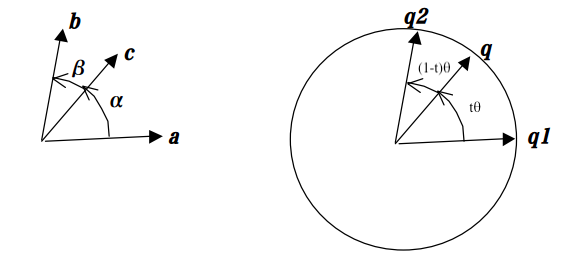
この式の意味を理解するために,まず簡単な幾何の定理を示します。ここでは,長さ1の3つのベクトル が,角度をなして並んでいます。
この3つのベクトルには、
の関係が成り立つことが知られています。この定理をふまえて、大円での断面図上に3つのQuaternion を描いたものを右に示しました.前述の定理から,Quaternion の大円補間の意味が理解できると思います。
(おしまい:最後まで読んで頂ありがとうございました。過去の記事から思考を再度トレースしてみましたが、数式のバグを2つ発見しました。)
(参考)Java と C++ のライブラリ
この辺りの数学を実装さした vecmath というライブラリをソースコードで公開しています。

コメント