テレビ番組の視聴率を調査するとき、何千万という世帯すべてを調査するのは時間とコストがかかりすぎてしまうので、現実的ではありません。
そのため、一般的には600程度の世帯をランダムに標本抽出し、その600世帯の中での視聴率(標本平均)を調べることで全体の視聴率(母平均)が推定されています。
「たった600世帯の調査で信用できるの?」と思うかもしれませんが、恣意性なく完全にランダムに標本抽出したのであれば、600世帯の標本平均はほぼ「母平均との誤差が約2%ポイントから4%ポイント以下におさまる」ことが分かっています。
このような、標本抽出にともなう誤差のことを標本誤差と言います。全体の視聴率が20%なら、600世帯の中での視聴率は95%の確率で約16.8%~23.2%の中におさまります。
小さな誤差とは言い難いですが、コストと実用性を天秤にかけて「600世帯の中での視聴率(標本平均)」を「全体の視聴率(母平均)の推定量」として利用しているのだと考えられます。
このように、推定においては「推定量」そのものと同じくらい「推定量の推定精度」がどのくらいなのかが重要になってきます。
この「推定量の推定精度」を表すのが、標準誤差です。
今回は、そんな標準誤差について解説していきます。
photo credit:flash.pro
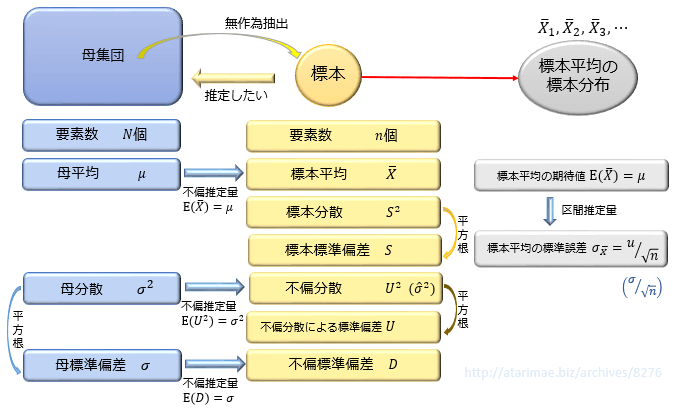
標準誤差とは何か?
標準誤差とは、広義では『推定量の標準偏差』のことを言い、標本から得られる推定量そのもののばらつきの大きさ・推定精度を表す指標として利用される数値です。
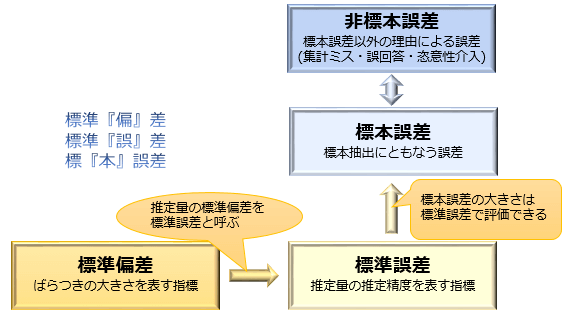
「〇〇の標準誤差」が小さい値であるほど、〇〇はばらつきが小さく精度の高い推定量であると評価されます。
基本的に「標本平均の標準誤差」について語られることが多く、この「標本平均の標準誤差」のことを単に『標準誤差』と省略して表記されていることが多いです。
これが、狭義の標準誤差となります。

「標準誤差は狭義には『標本平均の標本分布の標準偏差(=標本平均はどの程度ばらつくものなのか)』のことを指すが、広義には標本平均に限らずさまざまな推定量の標準偏差のことを『〇〇の標準誤差』と呼ぶ」とおさえておくと良いでしょう。
標準誤差の使い方。95%信頼区間とは?
ここからは、狭義の標準誤差(標本平均の標本分布の標準偏差)の使い方について述べていきます。
分布が正規分布に従う場合、
母平均の68%信頼区間は、「標本平均 ± 1×標準誤差」
母平均の95%信頼区間は、「標本平均 ± 2×標準誤差」で表されます。(正確には2でなく1.96)
これは、無作為標本抽出を繰り返し行えば100回に95回の割合で「標本平均 ± 2×標準誤差」内に真の平均(母平均 μ )を含んでいる、ということを意味します。
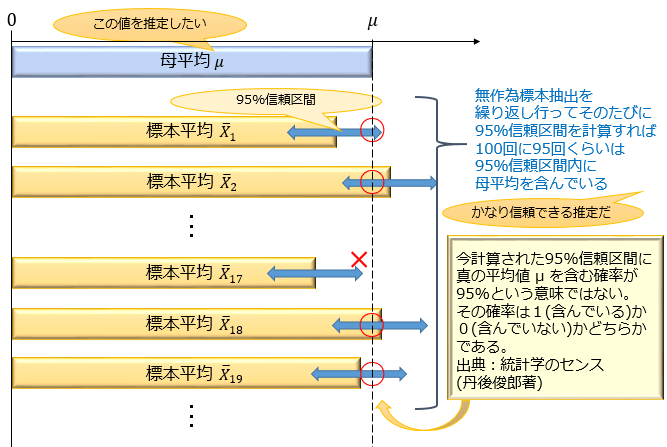
×よくある間違い:標本平均170cm,標準誤差0.5cmだから、母平均が169cm~171cmに含まれる確率は95%だ
◎正しい:標本平均が170cm,標準誤差0.5cmと求まった。無作為標本抽出を繰り返し行えば100回に95回の割合で「標本平均 ± 2×標準誤差」の中に母平均を含んでいるのだから、とりあえずは母平均が169cm~171cmの中に含まれると考えて問題ないだろう
95%信頼区間の考え方は勘違いしやすいので、注意しておきましょう。
〇:(次に行う無作為抽出の結果から計算される)95%信頼区間が母平均 μ を含む確率は95%
◎:無作為抽出を繰り返し行えば100回に95回の割合で95%信頼区間が母平均 μ を含む
×:今計算された95%信頼区間が母平均 μ を含む確率は95%
母平均は定数であり、確率的に変動することはありません。
確率的に変動するのは95%信頼区間の方です。
①次にサイコロを振ったら、出た目 ±2 以内に母平均=3.5を含む確率は66.7%
②サイコロを振ったら 4の目 (or 1の目) が出た。出た目 ±2 以内に母平均=3.5を含む確率は100%(or 0%)である
という2つの例を見比べればわかるように、今計算された信頼区間は母平均を「含んでいる」か「含んでいない」かのどちらかなので、「今計算された95%信頼区間が母平均を含む確率は95%だ」ということはできないのです。
測定者は母平均の値を知らないので、「含んでいる」か「含んでいない」かは分かりません。
それでも「無作為抽出を繰り返し行えば100回に95回の割合で95%信頼区間が母平均を含む」ことは分かっているので、「今計算された95%信頼区間が母平均を含んでいる」と信頼することには一定の合理性がありますよね。
このような、ある手法による推定がどの程度信頼できるのかに関する『推定精度の指標』が、標準誤差なのです。
100回に99回の割合で当たる推定をするには「標本平均 ± 2.58×標準誤差」(99%信頼区間)を利用します。
SEとSDの関係式。その正確な意味は?
統計書では「標準誤差はSE、標準偏差はSD」と表記され、以下の計算式が載せられていることが多いです。

この式から、「標準偏差を の正の平方根で割った値が標準誤差だ」と丸暗記されてしまうことが多いのですが、先に述べた通り標準誤差も1種の標準偏差なので、この認識は正確とは言い難いです。
この式を正確に述べると、互いに独立で同一の確率分布に従う個の確率変数 に対して
確率変数 の標準偏差
個の確率変数 の標本平均の標準偏差
となります。
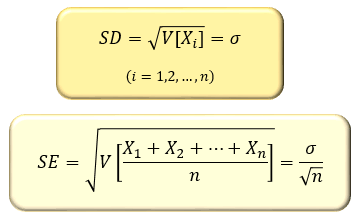
ただし、推定では母標準偏差 が未知の場合が多いので、実際の計算では を母標準偏差の推定値である『不偏分散による標準偏差(不偏分散平方根)』で代用するのが一般的です。
不偏分散平方根は、 又は で表します。 は「 の推定値である」という意味合いが強い表現です。

また、小標本()においては不偏分散平方根の「推定量としての精度」が悪くなり、「母標準偏差の推定値」として代用する根拠が弱くなるので、そのズレを考慮した t 分布で補完することになります。
※このように、標準誤差は『推定量の標準偏差の推定値』で代用されるケースが多いため、初めから標準誤差を『推定量の標準偏差の推定値』と定義する統計書もあります。基本的には両者に計算上の違いはありません。
参考文献
標準誤差については、1)のp92~107が特に参考になります。
1)山田剛史教授,村井潤一郎教授著『よくわかる心理統計』(ミネルヴァ書房)
2)浜田知久馬教授著『学会・論文発表のための統計学』(真興交易)
3)改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎(東京図書)⇒定義はp107,「信頼区間のよくある間違い」はp110を参照