ゼロで割ってはいけない理由を割り算の定義から考えるとこうなる

「 3×0=0$3\times 0=0$ 」「 (125＋69)×0=0$(125＋69)\times 0=0$ 」「 15984×28347×0=0$15984\times 28347\times 0=0$ 」

どんな値にかけても 0$0$ になってしまう数。ゼロ。

無いことを表す「 0$0$ 」という値には、不可解かつ神秘的な魅力を感じさせられます。

この「 0$0$ の不可解さ」をよく表しているのが、「 0$0$ で割ってはいけない」というルール。

「なんで 0$0$ で割ってはいけないの？」と先生に聞いても「そういうものだから」と言いくるめられ、モヤモヤした経験のある方も多いのではないでしょうか。

そこで今回は、「なぜ 0$0$ で割ってはいけないのか？」を割り算の定義から考えていきます。

割り算の定義から考える

皆さんは、割り算の定義＝「そもそも割り算とは何か？」と聞かれたら、どう答えますか？

「12$12$ 個のりんごを 4$4$ 人で分けた時の、1$1$ 人当たりのりんごの数？」

いいえ、それは割り算の使い方であって定義ではないんです。

By: kara

割り算は、代数的には以下のように考えることができます。今回はこれを利用しましょう。

実数などにおける定義から離れると、除法は乗法を持つ代数的構造について「乗法の逆元を掛けること」として一般化することができる。
参考：除法 – Wikipedia

これは、かみ砕いて言うと「割り算とは、逆数をかけることである」という意味です。

例えば

10÷5$10÷5$ とは、10$10$ に「 5$5$ の逆数である 0.2$0.2$ 」をかけること

12÷4$12÷4$ とは、12$12$ に「 4$4$ の逆数である 0.25$0.25$ 」をかけること

という意味になります。

「割り算」とは「逆数をかけること」である

ここから、0$0$ で割ってはいけない理由が見えてきます。

0で割るとはどういうことか？

「割り算」が「逆数をかける」ということは

「 0$0$ で割る」とは「 0$0$ の逆数をかける」という意味になります。

でも、0$0$ の逆数って何でしょう？

2$2$ の逆数は 1/2$1/2$

7$7$ の逆数は 1/7$1/7$

ということは、0$0$ の逆数は 1/0$1/0$？

そんな数、聞いたことがありませんよね。

事実、0$0$ に逆数は存在しません。0$0$ に何をかけても 1$1$ にはなりませんから。

そして、存在しないものは定義しようがありません。

「 0$0$ の逆数をかける」という行為自体が存在しないので、「 0$0$ で割る」ことも定義できない。

だから、「 0$0$ で割ってはいけない」んです。

1＝2の証明。存在してはいけない数

0$0$ には逆数が存在しないから、0$0$ で割ってはいけない。

なら、「 0$0$ には逆数がある」と無理やり定義してやればどうでしょう？

1/0$1/0$ という数の存在を認めれば、0$0$ で割ることもできるようになります。

が、しかし・・・

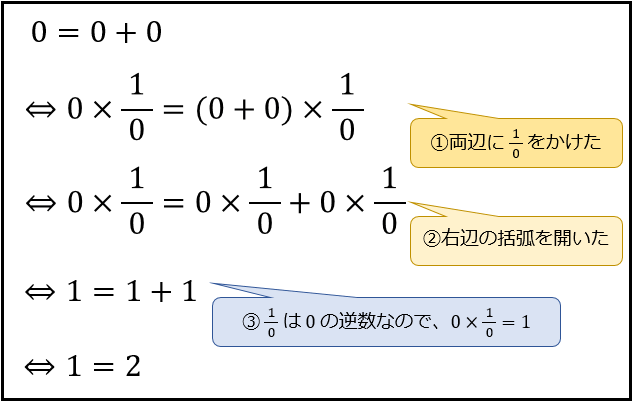
1/0$1/0$ という数の存在を認めたら、1=2$1=2$ というとんでもない等式が成立してしまいました。

Tooda Yuuto

1/0$1/0$ は、存在してはいけない数なんですね。

まとめ

①割り算とは「逆数をかけること」である

②つまり「 0$0$ で割る」とは「 0$0$ の逆数をかける」ことを意味する

③しかし、0$0$ には逆数がないので「 0$0$ の逆数をかける」という行為自体が存在せず、0$0$ で割ることを定義できない。だから 0$0$ で割ってはいけない

④裏を返せば、0$0$ に逆数が存在すると無理やり仮定すれば、0$0$ で割ることが可能になる。しかし、0$0$ に逆数が存在すると困ったことになる