はじめに
私はこれまで機械学習のパラメータチューニングに関し、様々な書籍やサイトで学習を進めてきました。
しかしどれもテクニックの解説が主体のものが多く、
「なぜチューニングが必要なのか?」
という目的に関する記載が非常に少なかったため、体系的な理解に苦労しました。
この経験を後世に役立てられるよう、「初心者でも体系的に理解できる丁寧さ!」をモットーに記事にまとめたいと思います。
具体的には、
1. パラメータチューニングの目的
2. チューニングの手順とアルゴリズム一覧
3. Pythonでの実装手順 (SVMでの分類を例に)
の手順で解説を進めます。
独自解釈も含まれるため、間違っている点等ございましたら指摘頂けると有難いです。
なお、文中のコードはこちらのGitHubにもアップロードしております。
1. パラメータチューニングの目的
1-1. パラメータチューニングの適用対象
1-2. 背景 ~機械学習の複雑化~
1-3. ハイパーパラメータとは何か?
1-4. チューニングの目的
について解説します。
本章は長いので、「早く実践に移りたい!」という方は、1-4まで飛んでいただければと思います
1-1. パラメータチューニングの適用対象
今回紹介するパラメータチューニングは、主に教師あり学習(回帰+分類)を対象とした手法となります
(例)
回帰:気温、湿度、曜日からアイスクリームの売り上げ(目的変数=数値)を予測する
分類:長さ、重さ、色から果物の種類(目的変数=クラス)を推定する
詳細は後述しますが、
パラメータチューニングの目的を端的に言うと、回帰・分類において
「複雑な推定」を「未知のデータでも推定性能が上がるよう調整」
することとなります。
1-2. 背景 ~機械学習の複雑化~
まずは回帰を例に解説します
回帰の中で最も単純な手法が、下図のような「線形回帰」です
例えば気象庁のサイトから下記のようなデータをダウンロードし、
※気温、気圧は1月の平均を使用
city,altitude,latitude,temperature,pressure
Asahikawa,119.8,43.75666667,-7.5,995.3
Sapporo,17.4,43.06,-3.6,1009.8
Morioka,155.2,39.69833333,-1.9,996.1
Sendai,38.9,38.26166667,1.6,1010.2
Nagano,418.2,36.66166667,-0.6,966.6
Matsumoto,610,36.24666667,-0.4,943.5
Karuizawa,999.1,36.34166667,-3.5,897.6
Kawaguchiko,859.6,35.5,-0.6,913.7
Fujisan,3775.1,35.36,-18.4,626.5
Tokyo,25.2,35.69166667,5.2,1011.4
Nagoya,51.1,35.16666667,4.5,1011.6
Takayama,560,36.155,-1.4,950.9
Osaka,23,34.68166667,6,1009.5
Fukuoka,2.5,33.58166667,6.6,1020.1
Kagoshima,3.9,31.555,8.5,1017.3
Amami,2.8,28.37833333,14.8,1019.6
Naha,28.1,26.20666667,17,1014.5
説明変数=標高(altitude)、目的変数=圧力(pressure)としてscikit-learnで線形回帰すると(参考)
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import pandas as pd
import numpy as np
df_temp = pd.read_csv(f'./temp_pressure.csv')
lr = LinearRegression() # 線形回帰用クラス
X = df_temp[['altitude']].values # 説明変数(標高)
y = df_temp[['pressure']].values # 目的変数(気圧)
lr.fit(X, y) # 線形回帰実施
plt.scatter(X, y, color = 'blue') # 説明変数と目的変数のデータ点の散布図をプロット
plt.plot(X, lr.predict(X), color = 'red')
plt.xlabel('altitude [m]') # x軸のラベル
plt.ylabel('pressure [hPa]') # y軸のラベル
plt.text(1000, 700, f'r2={r2_score(y, lr.predict(X))}') # R2値を表示
下図のようになります。
直線で綺麗に回帰できることが分かります(R2=0.996)
が!しかし、実際の現象はもっと複雑で、様々な工夫を凝らさないとうまく予測できない事が多いです。
これら「複雑な現象に対応する工夫」として、下記3種類の手法がよく使われます。
A. 多次元の説明変数
B. 非線形
C. 汎化性能の向上(正則化)
もちろん、これ以外の工夫もありますが、今回は代表例としてこの3つを紹介します。
A. 多次元の説明変数
例えば上の気象庁データで、
説明変数=標高(altitude)、目的変数=気温(temperature)とするとどうなるでしょうか?
X = df_temp[['altitude']].values # 説明変数(標高)
y = df_temp[['temperature']].values # 目的変数(気温)
lr.fit(X, y)
plt.scatter(X, y, color = 'blue')
plt.plot(X, lr.predict(X), color = 'red')
plt.xlabel('altitude [m]')
plt.ylabel('temperature [°C]')
plt.text(1000, 0, f'r2={r2_score(y, lr.predict(X))}') # R2乗値を表示
のようにうまく線形回帰できません。
気温には標高以外の要素(例えば緯度)も効いているようです。
そこで説明変数を緯度(latitude)とすると、
のように全体としては少し改善したように見えますが、
北緯36度付近(標高の高い地域が多い)の精度がイマイチであることがわかります。
精度が分かりやすいよう予測値と実測値をプロットしても、
import seaborn as sns
sns.regplot(lr.predict(X), y, ci=0, scatter_kws={'color':'blue'}) # 目的変数の予測値と実測値をプロット
plt.xlabel('pred_value') # 予測値
plt.ylabel('true_value') # 実測値
plt.text(0, -10, f'r2={r2_score(y, lr.predict(X))}') # R2乗値を表示
では標高と緯度を組み合わせて気温を推定するとどうなるでしょう?
感覚的には気温に効く2要素両方を考慮できるので、精度が上がると想像できます。
説明変数を標高(altitude)、緯度(latitude)の2次元として
(目的変数も合わせると3次元で)プロットしてみます
from mpl_toolkits.mplot3d import Axes3D
X = df_temp[['altitude', 'latitude']].values # 説明変数(標高+緯度)
y = df_temp[['temperature']].values # 目的変数(気温)
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter3D(X[:, 0], X[:, 1], y)
ax.set_xlabel('altitude [m]')
ax.set_ylabel('latitude [°]')
ax.set_zlabel('temperature [°C]')
この2次元の説明変数で線形回帰、予測値と実測値をプロットすると
lr.fit(X, y) # 線形回帰実施
sns.regplot(lr.predict(X), y, ci=0, scatter_kws={'color':'blue'}) # 目的変数の予測値と実測値をプロット
plt.xlabel('pred_value [°C]')
plt.ylabel('true_value [°C]')
plt.text(0, -10, f'r2={r2_score(y, lr.predict(X))}') # R2値を表示
のように、予測精度が大きく向上する(ほぼ予測値≒実測値)ことが分かります。
以上のように、一般的に複雑な現象を予測したいときは、
多次元の説明変数を組み合わせることで、推定性能が向上することが多いです
※ただし、可視化難易度や次元の呪いなど、次元数が増えることによるデメリットもあるので、むやみに増やしすぎるのは禁物です
B. 非線形
サンプルとして使用するデータを変えます。
こちらを参考に、動物の体長と体重の関係をプロットしてみました。
name,body_length,weight
Mara,72,12
Lion,210,200
Hyena,150,70
Eland,295,650
Wolf,115,35
Hippopotamus,420,3000
Bear,150,115
Tiger,250,300
Deer,150,85
Camel,300,700
Zebra,220,275
Rhinoceros,425,2550
Buffalo,275,750
Elephant,675,6650
Gorilla,180,170
Giraffe,480,900
df_animal = pd.read_csv(f'./animal_size.csv')
X = df_animal[['body_length']].values # 説明変数(体長)
y = df_animal[['weight']].values # 目的変数(体重)
plt.scatter(X, y, color = 'blue') # 説明変数と目的変数のデータ点の散布図をプロット
plt.xlabel('body_length [cm]')
plt.ylabel('weight [kg]')
他の動物と明確に傾向の異なるキリン(細長い‥笑)を除外して線形回帰してみます
df_animal = df_animal[df_animal['name'] != 'Giraffe'] # キリンを除外
df_animal = df_animal.sort_values('body_length') # 表示用に体長でソート
X = df_animal[['body_length']].values # 説明変数(体長)
y = df_animal[['weight']].values # 目的変数(体重)
lr.fit(X, y) # 線形回帰実施
plt.scatter(X, y, color = 'blue') # 説明変数と目的変数のデータ点の散布図をプロット
plt.plot(X, lr.predict(X), color = 'red')
plt.xlabel('body_length [cm]')
plt.ylabel('weight [kg]')
plt.text(350, 1000, f'r2={r2_score(y, lr.predict(X))}') # R2値を表示
データの傾向としては体長が大きいほど体重増加の傾きが大きくなる、曲線的な増加をしていますが、
無理やり線形で回帰しているため、イマイチなフィッティングとなっています。
物理法則から、体重(∝体積)は体長の3乗に比例すると予測されるため、
3次式で回帰すれば(2次以上は「多項式回帰」と呼びます)、この「曲線的な増加」を表現できると想像できます。
多項式回帰の方法には、scikit-learnを使う方法や、scipy.optimizeを使う方法等がありますが、
今回は物理法則に基づいて3乗以外の係数を無視するため、scipy.optimizeを使用します。
def cubic_fit(x, a): # 回帰用方程式
Y = a * x **3
return Y
popt, pcov = curve_fit(cubic_fit, X[:,0], y[:,0]) # 最小二乗法でフィッティング
plt.scatter(X, y, color = 'blue') # 説明変数と目的変数のデータ点の散布図をプロット
pred_y = cubic_fit(X, popt[0]) # 回帰線の作成
X_add = np.sort(np.vstack((X, np.array([[370],[500],[550],[600]]))), axis=0) # 線が滑らかになるよう、プロット用にデータ補完
pred_y_add = cubic_fit(X_add, popt[0]) # 回帰線の作成(プロット用)
plt.plot(X_add, pred_y_add, color = 'red') # 回帰線のプロット
plt.xlabel('body_length [cm]') # x軸のラベル
plt.ylabel('weight [kg]') # y軸のラベル
plt.text(400, 1000, f'r2={r2_score(y, pred_y)}') # R2乗値を表示
線形回帰と比べてフィッテングも良くなり、当てはまりの良さを表すR2値も向上していることが分かります。
3次式で非線形回帰したことで、推定性能が向上したと言えるでしょう!
上の例では「何乗に比例するか」を物理法則に基づき明示的に与えていますが、
実際の問題では明示的な式が分からない場合が多いです。
よく使われる機械学習アルゴリズムは、このような非線形のフィッティングを「実データに合わせて」「柔軟に」実現してくれる工夫が凝らされています(例:サポーベクターマシンにおけるカーネルトリック)
C. 汎化性能の向上(正則化)
一般的にモデルを複雑にして細かい部分まで合わせ込むと、学習データに対する性能は向上します。
ただ上の図を見ると、細かくフィッティングした線は「合わせ込みすぎでは?」という印象を受けるかと思います。
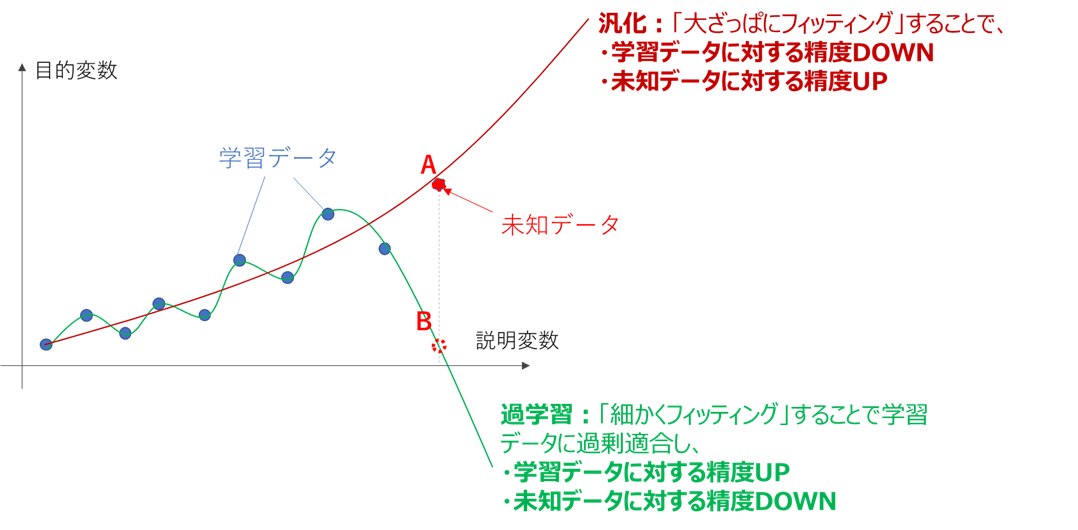
この「学習データに過剰に合わせ込んだ状態」を、過学習(Overfitting)と呼びます。
過学習の弊害は、未知データに対する推定性能が落ちる事にあります。
下図のように、過学習すると学習データの細かな変化を鋭敏に拾いすぎてしまい、学習データが存在しない部分、すなわち未知データの推定能力が落ちてしまいます。
過学習防止に多用される手法が、正則化です(詳細は別記事で投稿しています)
機械学習は、一般的に学習データに対する損失関数(例:最小二乗法での誤差二乗和)を最小化するよう学習しますが、
これだけでは細かくフィッティングした複雑なモデルが生成され、過学習が起こります。
そこで、損失関数にモデルの複雑さを表す指標(正則化項)を加え、これを最小化するよう学習すれば、
性能と複雑さ、すなわち過学習と未学習のバランスを取った学習が実現できます。
このとき、元の損失関数と正則化項をどの割合で足し合わせるかで、上記のバランスが決まるのですが、
このバランス変化はSVMにおけるパラメータ「C」の挙動を見ると、分かりやすいかと思います。
1-3. ハイパーパラメータとは何か?
機械学習のアルゴリズムは、前記3種類(多次元・非線形・汎化性)を始めとした機能を実現するため様々な工夫を凝らしていますが、
「どれくらい非線形か」や「過学習と未学習」などのバランスは、実際のデータに合わせて学習とは別途調整する必要があります。
これらのバランスを調整するためのパラメータを、ハイパーパラメータと言います
サポートベクターマシンでの例
分類における定番アルゴリズムの1つである「サポートベクターマシン(SVM)」を例に、ハイパーパラメータの役割を解説します。
詳細は別記事に記載しておりますが、サポートベクターマシンにはgammaとCという2種類のハイパーパラメータがあり、それぞれ以下の役割を果たしています。
・gamma:カーネルトリックによる非線形決定境界の調整 → 「B.非線形」に対応する工夫
・C:正則化項(ソフトマージン)の調整 → 「C.汎化性能の向上(正則化)」に対応する工夫
gammaやCを変えた時の決定境界の変化を以下に図示します。
gammaを変化させたとき
gammaが小さくなるほど曲率が小さくなって線形に近づき、gammaが大きくなるほど曲率が大きくなることが分かります。
ここからも、gammaが「どれくらい非線形か」を調整するパラメータであることが分かるでしょう
Cを変化させたとき
Cが大きいほど、誤分類は少ないがいびつな決定境界(過学習寄り)
Cが小さいほど、誤分類は多いが滑らかな決定境界(未学習=汎化寄り)
となっていることが分かります。
1-4. チューニングの目的
別記事に記載したSVMの例のように、機械学習は多種多様なアルゴリズムを通じて、「多次元」「非線形」「汎化性能」等の課題をクリアしています。
そして先人達の努力により、これらの課題は少数のハイパーパラメータに簡略化されて調整可能な形となっています(SVMではgammaとCの2個のパラメータ)
機械学習の性能をフル活用するためには、これらのパラメータを実際のデータに合わせチューニングする必要があります。
再現性のある調整をするためには、定量的な指標が必要となりますが、
分類:「誤分類の少なさ」を表す指標
回帰:「誤差の小ささ」を表す指標
となるような性能指標を最大化するようチューニングすることが、一般的な手法となります。
性能指標の具体例については、2章で解説します。
学習データとテストデータ
1-2-Cで触れましたが、下図のように学習データに対する性能指標を最大化しようとすると過学習状態となり、未知データに対する推定能力が低下します
機械学習の実運用時は、未知のデータに対する能力が重要となるので、これは喜ばしくない状況です。
この過学習を防ぐために、下図のように手持ちのデータを学習データとテストデータに分け、テストデータに対する性能指標を最大化するようパラメータチューニングを行うことが一般的です。
テストデータは学習に使用していないため、未知データに対する性能評価を模擬することができ、
過学習を防いで未知データに対する推定能力を上げることができます。
学習データとテストデータの分割法はクロスバリデーションと呼ばれる手法が一般的ですが、こちらも2章で解説します。
パラメータチューニングの目的
以上、パラメータチューニングの目的をまとめると、
ハイパーパラメータで非線形性や汎化性能のバランスを調整することで、未知データに対する推定性能を最大化する
となります
2. チューニングの手順とアルゴリズム一覧
前述のように、パラメータチューニングの手順を端的に言うと
データを学習データとテストデータに分け、
テストデータに対する性能指標を最大化するようチューニングする
となりますが、この手順をフローチャート化すると下図のようになります。
特に重要となる赤字部分に関して、詳細に解説します。
2.1 評価指標の定義
前述のように、評価指標は
分類:「誤分類の少なさ」を表す指標
回帰:「誤差の小ささ」を表す指標
を使用することが望ましいです。
分類、回帰それぞれについて、よく使われる指標とその特徴を列記します。
(scikit-learnで使用可能な指標一覧はこちら参照)
なお、これらの指標は、
大きい方が性能が良い指標:Accuracy、R2など
小さい方が性能が良い指標:RMSE、LogLossなど
の2種類が存在し、前者は最大化、後者は最小化する必要がある事にご注意ください
(scikit-learnでは後者は自動でマイナスを取ってくれるので、正負の方向をあまり気にしなくともチューニングができます)
A. 分類の評価指標
よく使われる分類の評価指標を列記します。
| 名称 | 和名 | scikit-learnでの名称 | 性能の良い方向 | メリット | デメリット |
|---|---|---|---|---|---|
| Accuracy | 正解率 | accuracy | 大きいほどGood | 適合率と再現率のバランスが見られる | 不均衡データに弱い |
| Precision | 適合率 (精度) | precision | 大きいほどGood | 偽陽性(見すぎ)を評価できる | Recallとトレードオフ |
| Recall | 再現率 | recall | 大きいほどGood | 見逃しを評価できる | Precisionとトレードオフ |
| F1-score | f1 | 大きいほどGood | 不均衡データに強い | PR-AUCより汎化性に劣る | |
| LogLoss | 交差エントロピー損失 | neg_log_loss | 小さいほどGood | 正誤の度合いを連続的に評価できる | 他データとの性能比較できず&確率算出が必要 |
| AUC | roc_auc | 大きいほどGood | 他データとの性能比較ができる | 計算量多い&確率算出が必要 | |
| PR-AUC | average_precision | 大きいほどGood | 不均衡データに強い | 計算量多い&確率算出が必要 |
どれがいいの?
基本:LogLoss
他データと性能比較したい場合:AUC
各クラスのデータ数偏り大(不均衡データ)※:PR-AUCまたはF1-score
多クラスかつ不均衡データ※:F1_macroまたはroc_auc_ovo
多クラスかつ不均衡でない:F1_microまたはroc_auc_ovr
※不均衡データのチューニング時は、分類器側にも引数「class_weight="balanced"」が必要です(参考)
その他指標選択時の諸注意は、こちらをご参照ください
具体的な算出式
※LogLossと確率
LogLossの式におけるpはそのクラスに所属する確率です。
クラス所属確率を算出できる分類手法はロジスティック回帰が代表的です。
scikit-learnでは前述のSVMにも確率を求めるメソッドがありますが、本来のSVMのアルゴリズムとは別に確率算出アルゴリズムを後付けで付加しているようです。
同様にscikit-learnの大半の分類アルゴリズムには、後付けの確率計算メソッド"predict_proba"があり、これらを利用してLogLossを算出できます。
私見となりますが、AccuracyやF1など分類の評価指標は離散的な値を取るものが多く、データ数が少ないとき多くのパラメータで評価指標が同値となり、真に性能が高いパラメータを見出すのが難しくなります。
一方でLogLossは連続的な値を取るため、データ数が少ない時もパラメータ間の性能差を鋭敏に評価できるため、多くのケースで推奨される指標なのだと思います。
※AUCとPR-AUCの算出式
基本的には、PrecisionとRecallはトレードオフ関係にあります。
このトレードオフの変化を見る手法として、ひとつは前述のF1-Score、もうひとつが下図のようなROC曲線です
ROC曲線は、閾値を変化させて、TPR(見逃しの少なさ)とFPR(見すぎの多さ)の変化をプロットしたものとなります。
ROC曲線の内部の面積をAUCと呼び、前述のトレードオフを考慮した評価指標としてよく利用されます。
scikit-learnにおいては、LogLossのときと同様のクラス所属確率において、確率何%に閾値を引くかを変化させ、ROC曲線およびAUCを算出しています。
また、ROC曲線の代わりに、縦軸にPrecision、横軸にRecallをプロットしたPR曲線もあり、
PR曲線の内部の面積をPR-AUCと呼び、不均衡データの評価指標としてよく利用されます。
B. 回帰の評価指標
よく使われる回帰の評価指標を列記します(参考)
| 名称 | 和名 | scikit-learnでの指定法 | 性能の良い方向 | メリット | デメリット |
|---|---|---|---|---|---|
| R2-score | 決定係数 | r2 | 大きいほどGood | モデルの当てはまりの良さを見られる | 注意点4参照 |
| RMSE | 平均二乗誤差平方根 | neg_mean_squared_error | 小さいほどGood | 全データにバランスよくフィット | 外れ値の影響をやや受けやすい |
| MAE | 平均絶対誤差 | neg_mean_squared_error | 小さいほどGood | 外れ値の影響を受けにくい | RMSEより最大誤差が大きくなる傾向 |
| RMSLE | 平均二乗対数誤差平方根 | neg_mean_squared_log_error | 小さいほどGood | 注意点3参照 | 正負に対し不公平な評価となる |
どれがいいの?
基本:RMSE
外れ値を無視したいとき:MAE
注意点3に該当するとき:RMSLE
その他指標選択時の諸注意は、こちらをご参照ください
具体的な算出式
に基づき、下式で算出します。
2.2 パラメータ種類と探索範囲の選択
「パラメータチューニングは経験が重要な職人芸」と言う人がいますが、
そう言われる所以のひとつがこの部分です。
例えば先述のSVMの場合、CとGammaという2つのパラメータを調整するのですが、
「Cは0.01~100の間、Gammaは0.0001~0.1の間」
というように、事前にパラメータの探索範囲を定義する必要があります
また、SVMはパラメータ数が2個ですが、XGBoostのように10個を超えるような場合、そのまま調整すると指数関数的に所要時間が増えるため、パラメータ種類を絞る必要があります。
これらパラメータ種類と範囲の選択法に言及した書籍や記事は非常に少なく、経験に基づいて決める必要があります。
天下のgoogleさんも「すべてのケースに当てはまるアドバイスというのはほとんどありません」と言っています
私自身もこの工程に精通しているわけではないですが、以下の2通りの手法で、初心者でもある程度目星が付けられると考えています
先例の調査
他力本願な手法ですが(笑)、私の経験上、複数の先例を探してそれらの間をとって選択すれば、それなりに良い探索範囲を決められることが多かったです。
検証曲線
探索範囲指定に関しては、検証曲線を使用して目星をつけることができます(参考)
具体的な実装方法は後述します。
2.3 パラメータの組合せを選択
一般的に「パラメータチューニング」の手法として紹介されているのは、この部分です。
組合せの選択法には、主に下記3種類のアルゴリズムがあります。
| 名称 | 概要 | メリット | デメリット | ライブラリ | |
|---|---|---|---|---|---|
| A | グリッドサーチ | パラメータを格子状に総当たり | シンプルで結果解釈性が高い | 計算時間がかかる | Scikit-Learn |
| B | ランダムサーチ | パラメータをランダムに決定 | 平均的にはグリッドサーチより速い | 運任せの要素あり | Scikit-Learn |
| C | ベイズ最適化 | 前回結果に基づきパラメータ決定 | ランダムサーチより速い | ライブラリ操作がやや難 | BayesianOptimization, Optuna |
※上記以外にも遺伝的アルゴリズム等があるが、機械学習用途ではあまり使用されない
※ランダムサーチの詳細および画像出典はこちら
※ベイズ最適化の画像出典
それぞれ具体的に解説します
A.グリッドサーチ
予め指定したパラメータの組合せを格子状に総当たりで走査します。
例えば、先ほど紹介したSVMの場合、gammaとCの2種類のパラメータが存在しますが、
gammaの組合せ = [0.01, 0.1, 1, 10]
Cの組合せ = [0.1, 1, 10]
を予め指定すると、以下の①~⑫のパラメータの組合せを総当たりで走査し、それぞれで2.1で指定した評価指標をクロスバリデーション(2.4で後述)で算出します。
全ての組合せの中から評価指標が最も良いパラメータを採用すれば、チューニング完了となります。
グリッドサーチはパラメータの値を直接指定できるので、
解釈性の高さや経験を活かしやすいことが魅力です。
一方で、パラメータ数に対して組み合わせ数が指数関数的に増えるため、パラメータ数が多いXGBoostやLightGBMなどの学習器では非常に時間が掛かる事がデメリットです。
グリッドサーチのライブラリ
簡単なアルゴリズムなのでスクラッチでも実装できますが、Scikit-Learnにクロスバリデーションと一括で処理可能な"GridSearchCV"クラスがあるので、これを利用するのが便利かと思います
B.ランダムサーチ
ある範囲の中から、ランダムにパラメータの組合せを生成します。
scikit-learnでは下図のように、予め指定したパラメータの組合せから、ランダムに数点選びます。
グリッドサーチと同様、選んだ数点のうち評価指標が最も良いパラメータを採用すれば、チューニング完了となります。
ランダムサーチは平均的にはグリッドサーチよりも効率よく探索が出来ると言われており、
チューニングの高速化が魅力です。
ランダムサーチのライブラリ
簡単なアルゴリズムなのでスクラッチでも実装できますが、Scikit-Learnにクロスバリデーションと一括で処理可能な"RandomizedSearchCV"クラスがあるので、これを利用するのが便利かと思います
C.ベイズ最適化
グリッドサーチは最初に決め打ちしたパラメータの組合せに左右され、ランダムサーチはランダムで探索するため、どちらも運任せ要素の強いアルゴリズムと言えます。
これに対しベイズ最適化は、前回までの評価結果を基に良いスコアの可能性が高い位置を推定し、次のパラメータの組合せとするため、前記探索法よりも根拠に基づいた効率的な探索ができるアルゴリズムと言えます。
ベイズ最適化のアルゴリズム
前述のように「良いスコアの可能性が高い位置」を推定する必要がありますが、
この推定に「ガウス過程」を使用します。ガウス過程とは、出力が入力を変数とした正規分布で表されるプロセスであり、その性質を利用して「ガウス過程回帰」と呼ばれる回帰手法に用いられています。
このガウス過程回帰の学習にベイズ推定を用いるため、「ベイズ最適化」と呼ぶようです。
ガウス過程回帰に関しては私も完全に理解しているわけではないので割愛しますが、
こちらやこちらで解説されており、厳密に理解されたい方は下記の書籍を購入するのが良いかと思います。
ガウス過程回帰の特徴に、出力として平均と標準偏差が得られる事が挙げられます。
詳細は後述しますが、この平均と標準偏差を使って「良いスコアの可能性が高い位置」を推定します。
また、ガウス過程以外にも、TPE (Tree-structured Parzen Estimator)と呼ばれる手法を用いた最適化が現在主流となりつつあるようです。
私は全く追えていませんが、こちらの記事で詳細に解説されています
獲得関数による探索位置の決定
「良いスコアの可能性が高い」ことを表す指標が、獲得関数(Acquisition Function)です。
ガウス過程回帰では目的変数予測値(ベイズ最適化の場合は2.1の評価指標予測値)の「平均」と「標準偏差」が求められますが、説明変数(ベイズ最適化の場合はチューニング対象のパラメータ)が1次元の場合の出力を図示すると以下のようになります。
図を見ると、学習データ(探索済のパラメータ)の近傍では標準偏差が小さく、離れるほど標準偏差が大きくなることが分かります。
前者は正解が分かっている学習データの近くなので予測の確度が高い、後者は学習データから遠いので予測があいまい、と解釈すれば、感覚と一致するかと思います。
探索の方針として、予測平均が大きい位置を探す("活用"と呼びます)ことはもちろん重要なのですが、これだけだと現在の最大値付近を延々探し続けて局所解に陥ってしまうので、未知の部分 = 標準偏差が大きい位置を探す("探索"と呼びます)ことも重要となります。
よって獲得関数は、平均と標準偏差を組み合わせる事により、"活用"と"探索"のバランスをとった関数とします。
獲得関数を決めるための方針としては、以下の3種類があります
(各方針での具体的な計算法はこちらが分かりやすいです)
| 名称 | 概要 | 特徴 |
|---|---|---|
|
PI (Probability of Improvement) |
現在の最大値を超える確率が最も高い点を選ぶ | 局所解に陥りやすい |
|
EI (Expected Improvement) |
現在の最大値との差の期待値が最も高い点を選ぶ | バランスが良い |
|
UCB (Upper Confidence Bound) |
上側信頼区間が最も高い点を選ぶ | EIと近い傾向 |
それぞれの探索法を簡単に解説します。
・PI (Probability of Improvement)
現在の最大値を超える確率が最も高い点を選ぶ方法です。
下図のようなイメージで獲得関数を求めます
PIは他の手法よりも"活用"が重視されるため、現在の最大値付近を集中探索しがちで、局所解に陥りやすいと言われています
・EI (Expected Improvement)
うまく表現できるグラフが思い付かなかったので図は割愛しますが。
現在の最大値との差の期待値が最も高い点を選びます。
PIよりも局所解に陥りづらいと言われています。
・UCB (Upper Confidence Bound)
現在の最大値を超える確率が最も高い点を選ぶ方法です。
下図のようなイメージで獲得関数を求めます(上側信頼区間は1σや95%信頼区間等を指定)
UCBはEIと似た傾向の探索となると言われています。
BayesianOptimizationライブラリでは、このUCBがデフォルトとなっています。
パラメータ2個におけるベイズ最適化のGifアニメ
ベイズ最適化の進行イメージがつかみやすいよう、
BayesianOptimizationライブラリ公式より、平均(Gausian Process Predicted Mean)と標準偏差(Gausian Process Variance)からUCB方針で求めた獲得関数(Acquisition Function)のGifアニメを下記します。