2021.2.15追記

先程運営様より、この記事についての連絡をいただきました。多くの方からの通報があったようです。不快な気分にさせた方々、大変申し訳ありませんでした。

これを受けまして、この記事はあと1週間で見られなくなることになります。修正すれば良いとのことですが、修正点がこの記事の本質なので、修正は諦めました。

美というものは死と隣り合わせに描かれることが数多くあります。桜の樹の下には屍体が埋まっているように、この美しいフラクタルの根本には削除依頼が埋まっていたようです。しかし、消えゆくことこそがまたその美を一段階深くするということもありましょう。いや、消えることそれこそが、美を永遠とする唯一の道かもしれません。ちんフラは、削除されることで初めて、全てがコンテンツ化された現代へのアンチテーゼとして、その本来の美しさを、余すところなく燦然と放つようにも思います。
燃えゆく金閣寺を眺める心持ちで、消えゆくこの美しきフラクタルを眺めようと思います。

再会

私とそれとの運命的な再会は、2019年の12月に遡る。フラクタル。それまでは存在を知っているに過ぎなかったその幾何学的な概念は、ある野菜の仲立ちによって、私の中に確固たる地位を占めるようになった。
野菜の名は、ロマネスコ。

見よ！自然が生み出したこの完璧な自己相似の造形を！目にした者の心を鷲掴みにして離さないこの魔力は、まさに10~12世紀の宗教美術を牽引したロマネスク芸術の名を冠するに相応しい。
ロマネスコを知ったのは、確か会社帰りの電車内のことだった。間近に控えたスターウォーズ・スカイウォーカーサーガ完結編の公開を前に、期待に胸を踊らせていた私であったが、ロマネスコの威光を前にしては、名だたるジェダイも無力であると感じたことを覚えている。ロマネスコの力を借りて、私は、フラクタルという美を確かに理解した。そこに悠久なものの影を感じたのである。

フラクタルとは

この記事の最終的な目標は、ち◯ち◯をフラクタルにすることである。その前に今一度、フラクタルの概念を簡単におさらいしておこう。なお私は化学系技術者であり、フラクタルをはじめとする幾何学は全くの専門外であるため、以下の記述の厳密性・正確性については目をつむっていただきたい。いや断じて看過できんという方は、ロマネスコを見て欲しい。この美しさの前では、私の記述の正誤など取るに足らないはずだから。

フラクタルとは

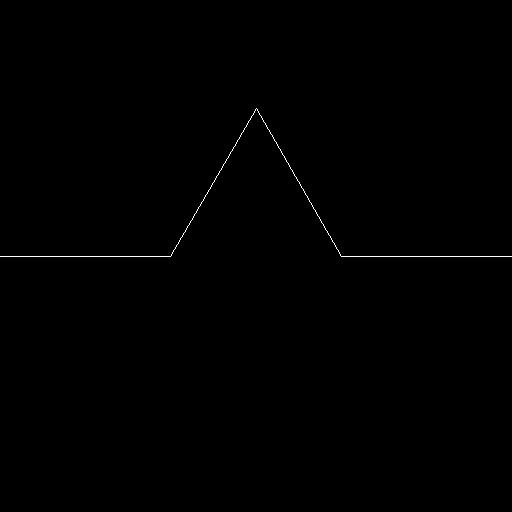
フラクタルは、図形の一部分と全体とが自己相似であるものを指す。フランスの数学者、マンデルブロが導入した、比較的新しい概念である。有名な例として、以下のコッホ曲線がある。

これは、ある一つの線分に対し、
　1. 線分を3等分する
　2. 分割した2点を頂点とする正三角形を描く
　3. 上記を無限に繰り返す
ことで得られる。

他にもシェルピンスキーのギャスケット、マンデルブロ集合、カントール集合など、枚挙に暇がない。
フラクタルの近似的な例は、自然界に数多く存在する。先に述べたロマネスコの形状をはじめとして、血管の分岐構造や腸の内壁、海岸線などはフラクタル構造である。

フラクタル次元

一般に、0次元は点、1次元は線、2次元は面、3次元は空間である。これは、位相次元という定義に基づく考え方である。一方これを長さ・面積・体積という観点から考えてみると、興味深いことが見えてくる。
0次元、すなわち点は、長さ・面積・体積いずれも0である。1次元(線)の場合、面積・体積は0であるが、長さが存在する。2次元(面)になると、体積は0であるが面積が存在する。その代わり、長さは無限大であると言える。

さてこの場合、先程のコッホ曲線について考えてみよう。作り方から考えると、コッホ曲線は無数の線分から成る図形であるから、面積・体積はもちろん0である。一方長さを考えると、有限の長さを持つ線分が無限に存在するため、これは無限の長さを有することを意味する。つまり、
　・1次元(長さ：有限、面積：0)
　・??次元(長さ：無限、面積：0)　←コッホ曲線
　・2次元(長さ：無限、面積：有限)
であり、コッホ曲線の次元は1次元でも2次元でもないことになる。
このような発想から次元を考えることで、フラクタル次元を定義することができる。具体的には、元の構造が、線形サイズ $ϵ$ の構造 $N (ϵ)$ 個で表されるとき、そのフラクタル次元は、

D = lim_{ϵ \to 0} \frac{\log N (ϵ)}{\log \frac{1}{ϵ}}

で与えられる。
コッホ曲線の場合、1/3に縮めると、4つの自己相似構造が必要になるため、

D = lim_{k \to \infty} \frac{\log 4^{k}}{\log 3^{k}} \approx \frac{\log 4}{\log 3} \approx 1.26

となる。

究極のフラクタルを作る

勘の良い読者はすでにお気づきのことであろうが、このフラクタルの美しさを極限まで高めるのが、他でもないち◯ち◯である。そこで、以下ではPythonを用いてち◯ち◯フラクタル(以下、ちんフラと呼ぶ)を描画することを試みる。

練習〜コッホ曲線の描画〜

練習としてコッホ曲線をPythonで描画してみよう。なお私はPythonについても素人であるため、ほとんどをゼロから学ぶPythonを参考にした。以下の記述で不明瞭な点があれば、ゼロから学ぶPython(リストとタプル)を参考にされたい。

モジュールのインポート

まずは必要なモジュールをインポートしよう。

import numpy as np
from PIL import Image,ImageDraw

関数の準備

コッホ曲線はすでに述べたように、線分を3等分し、分割した2点を頂点とする正三角形を繰り返し描いていくことで描画することができる。これを一般化して考えると、以下の手順でフラクタルを描画できることになる。
　A. 線分(入力ベクトル)を用意する
　B. お手本(変換ベクトルリスト)にしたがって線分を変換する
　C. 上記操作を繰り返す
コッホ曲線におけるお手本は、[(1,0), (0.5, $\sqrt{3}$ /2), (0.5,- $\sqrt{3}$ /2), (1,0)]とおけるだろう。一方の入力ベクトルは、さまざまな長さ・向きを持つ。そこで、
　a. 入力ベクトルの長さ・向きを求める
　b. お手本の長さ・向きを入力ベクトルに揃える
　c. 全入力ベクトルについて上の操作を行う
とすれば、コッホ曲線が描画できるはずである。
これをPythonで実装してみよう。

まず、入力とお手本の長さを揃えるために、お手本の長さを求める関数を用意する。

def length(vecs):
    x,y=0,0
    for (dx,dy) in vecs:
        x += dx
        y += dy
    return np.sqrt(x**2+y**2)

例えば変換ベクトルリストが[(1,0), (0.5, $\sqrt{3}$ /2), (0.5,- $\sqrt{3}$ /2),(1,0)]の場合、

\sqrt{(1 + 0.5 + 0.5 + 1)^{2} + (\sqrt{3} / 2 - \sqrt{3} / 2)^{2}} = 3

が得られる。

続いて、お手本の長さ・向きを入力ベクトルに揃える関数を作る。これによって得られるベクトルリストが、入力ベクトルの変換後の形である。

def convert(input_vec,conv):
    #入力ベクトルの長さを求める
    input_x,input_y = input_vec
    input_length = np.sqrt(input_x**2+input_y**2)
    #入力ベクトルの傾きを求める
    cos = input_x/input_length
    sin = input_y/input_length

    #入力ベクトルとお手本の長さの比を求める
    scale = input_length/length(conv)

    #お手本の長さを入力ベクトルに揃える
    temp = [(scale*x,scale*y) for (x,y) in conv]

    #tempの向きを入力ベクトルに揃える(回転行列をかける)。
    #これで得られるのが、変換後の形である。
    output = [(cos*x-sin*y,sin*x+cos*y) for (x,y) in temp]

    return output

最後に、入力ベクトルの集合が与えられた時に、それぞれの入力について上記関数を適用するような関数を用意する。この関数を実行すれば、さまざまなフラクタルが得られることになる。

def apply(input_vecs,conv):
    r = []
    for input_vec in input_vecs:
        r += convert(input_vec,conv)
    return r

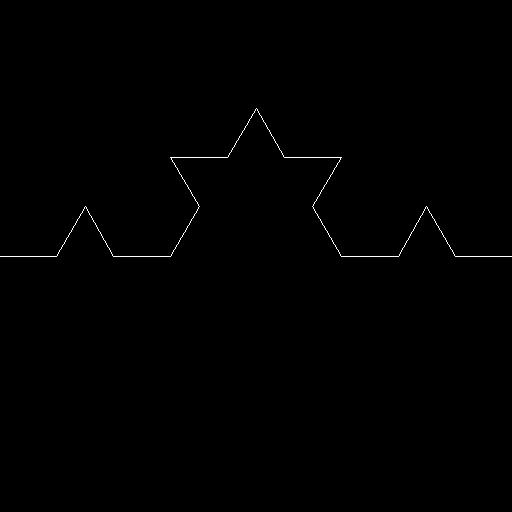
ではこれらの関数を用いて、コッホ曲線を描画してみよう。描画にはPILを用いている。繰り返しの回数はNで表す。

def draw_line(draw,input_vecs,size):
    x1,y1 = 0,0
    for (dx,dy) in input_vecs:
        x2 = x1 + dx
        y2 = y1 + dy
        draw.line((x1,size/2-y1,x2,size/2-y2),fill=(255,255,255))
        x1,y1 = x2,y2

size = 512
N = 1
img = Image.new("RGB",(size,size))
draw = ImageDraw.Draw(img)
input_vecs = [(size,0)]
conv = [(1,0),(0.5,np.sqrt(3.0)/2),(0.5,-np.sqrt(3.0)/2),(1,0)]

for _ in range(N):
    input_vecs = apply(input_vecs,conv)

draw_line(draw,input_vecs,size)
img

まずN=1の場合、

続いてN=2の場合、

一気にN=5まで進めてみると、

確かにコッホ曲線が描画できた。

本番〜ちんフラの描画〜

いよいよ本番である。
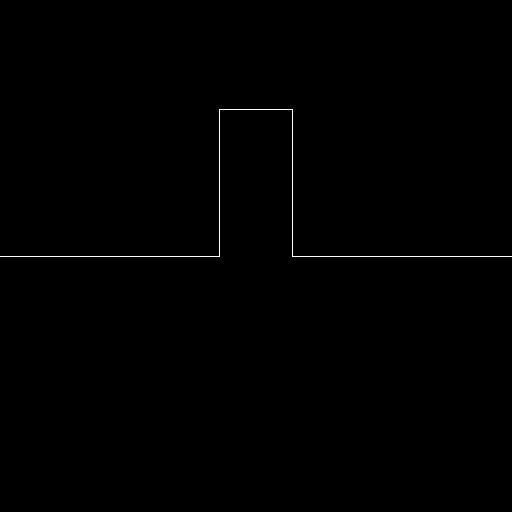
まず、お手本となる変換ベクトルリストを、[(6,0),(0,-4),(2,0),(0,4),(6.0)]としてみよう。これを用いてN=1で描画すると、次のようになる(ここではやや異なるスクリプトで描画しているが、混乱を避けるため記載しない)。

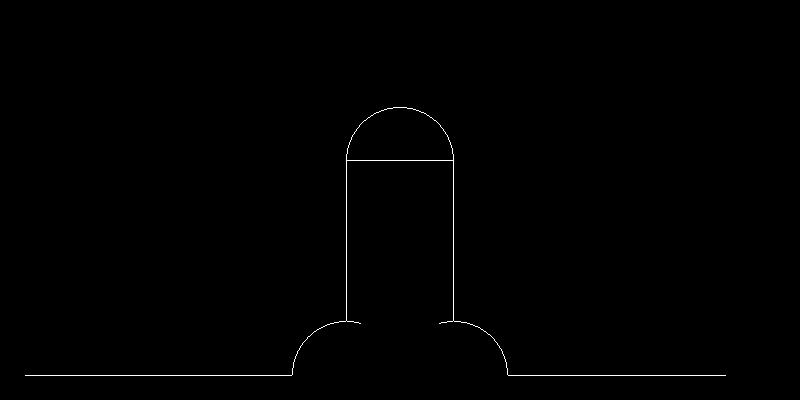
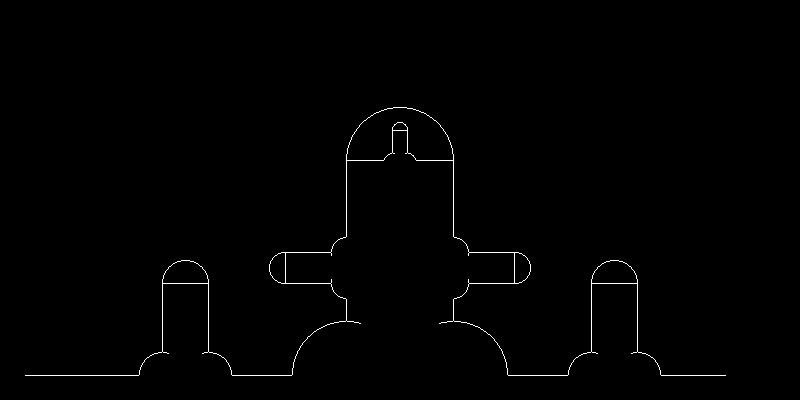
この長方形の適切な位置に扇形や半円を描画し、さらに余計な線分を消すと、1本のち◯ち◯を描画することができる。これが、N=1のときのちんフラであるといえる。

あとはこれを繰り返せばよい。つまり、
　1. 変換ベクトルリストを元にして長方形からなるフラクタル構造を作る
　2. 長方形の角に扇形や半円をくっつけ、ち◯ち◯の構造を作る
　3. 余計な線分を消す
という作業の繰り返しによって、ちんフラ描画することができる。

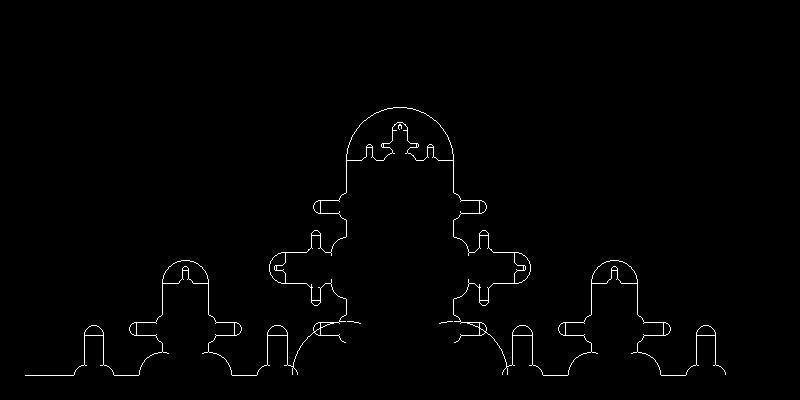
いよいよ、N=2,3,5の時のちんフラである。刮目せよ。

N=2のとき

N=3のとき

N=5のとき

見るものを敬虔な心持ちにさせる、圧倒的な美しさである。葛飾北斎の神奈川沖浪裏、ガウディのサグラダファミリア、その他人類の生み出した至高のフラクタルたちに引けを取らない、紛うことなき完璧な造形ではあるまいか。私はこれを描画を成し遂げたあと、しばし放心状態のまま動くことができなかったほどである。

以下は、ちんフラを描画するためのスクリプトである。コッホ曲線のときのdraw_line関数以後を書き換えた。力技であるが、素人が短い休日を使って作るにはこれが限界である。より効率的かつ賢明なち◯ち◯フラクタルの描画方法がある場合には、ぜひご教授願いたい。

def draw_chinfra(draw,a,size):
    x1, y1 = 25, 375
    count = 0
    flag = 0
    erase_list = []
    for (dx, dy) in a:
        x2 = x1 + dx
        y2 = y1 + dy
        if flag==0 or flag==4:
            flag = flag+1
        else:
            draw.line((x1,y1,x2,y2), fill=(255,255,255))
            flag = flag+1
        count = count+1
        if count==1:
            if dx>0:
                draw.arc([(x2-dx/6,y2-dx/6),(x2+dx/6,y2+dx/6)],180,285)
                erase_list.append((x2,y2,x2,y2-dx/6))
            elif dx<0:
                draw.arc([(x2+dx/6,y2+dx/6),(x2-dx/6,y2-dx/6)],0,105)
                erase_list.append((x2,y2,x2,y2-dx/6))
            else:
                if dy<0:
                    draw.arc([(x2+dy/6,y2+dy/6),(x2-dy/6,y2-dy/6)],90,195)
                    erase_list.append((x2,y2,x2+dy/6,y2))
                else:
                    draw.arc([(x2-dy/6,y2-dy/6),(x2+dy/6,y2+dy/6)],270,375)
                    erase_list.append((x2,y2,x2+dy/6,y2))

        if count==3:
            if dx>0:
                draw.arc([(x2-dx,y2-dx/2),(x2,y2+dx/2)],180,360)
            elif dx<0:
                draw.arc([(x2,y2+dx/2),(x2-dx,y2-dx/2)],0,180)
            else:
                if dy<0:
                    draw.arc([(x2+dy/2,y2),(x2-dy/2,y2-dy)],90,270)
                else:
                    draw.arc([(x2-dy/2,y2-dy),(x2+dy/2,y2)],270,450)

        if count==5:
            if dx>0:
                draw.arc([(x2-dx-dx/6,y2-dx/6),(x2-dx+dx/6,y2+dx/6)],255,360)
                erase_list.append((x2-dx-dx/2,y2,x2-dx+dx/6,y2))
                erase_list.append((x2-dx,y2,x2-dx,y2-dx/6))
            elif dx<0:
                draw.arc([(x2-dx+dx/6,y2+dx/6),(x2-dx-dx/6,y2-dx/6)],75,180)
                erase_list.append((x2-dx-dx/2,y2,x2-dx+dx/6,y2))
                erase_list.append((x2-dx,y2,x2-dx,y2+dx/6))
            else:
                if dy<0:
                    draw.arc([(x2+dy/6,y2-dy+dy/6),(x2-dy/6,y2-dy-dy/6)],165,270)
                    erase_list.append((x2,y2-dy-dy/2,x2,y2-dy+dy/6))
                    erase_list.append((x2,y2-dy,x2+dy/6,y2-dy))
                else:
                    draw.arc([(x2-dy/6,y2-dy-dy/6),(x2+dy/6,y2-dy+dy/6)],-15,90)
                    erase_list.append((x2,y2-dy-dy/2,x2,y2-dy+dy/6))
                    erase_list.append((x2,y2-dy,x2+dy/6,y2-dy))
            count = 0
            flag = 0

        x1,y1 = x2,y2

    for i in erase_list:
        draw.line(i,fill=(0,0,0))

size=800
N = 5
img = Image.new("RGB", (800, 400))
draw = ImageDraw.Draw(img)
a = [(750,0)]
draw.line((25,375,725,375))
b = [(6,0),(0,-4),(2,0),(0,4),(6,0)]
for _ in range(N):
    a = apply(a, b)
    draw_chinfra(draw, a, size)

img

おわりに

ち◯ち◯とフラクタル。決して交わることのなかった両者が幾何学の世界で相見えるとき、究極の美が現前する。数学者の岡潔は、その著作「春宵十夜」の中で、真善美は実在感であると述べた。ち◯ち◯フラクタルを前にした人間は、その無限の細部にまで確かにち◯ち◯が「在る」という、まぎれもない実在感に圧倒されるのである。これこそがち◯ち◯フラクタルの美の源泉であろう。細部に宿るのは神ではなく、ち◯ち◯なのである。