Infix Prefix Postfix Conversion (Stack)
Why we use Postfix Prefix & Infix
Postfix, Prefix expressions are faster to execute for the compiler than simple infix expression, as the compiler doesnt have to care about operator predence in case of postfix and prefix.


Introduction
- Operation : Any Expression of algebraic format (Example : A + B)
- Operands : A and B or 5 & 6 are operands
- Operators : +. -, %,*,/ etc are operators
Infix Notation
Infix is the day to day notation that we use of format A + B type. The general form can be classified as (a op b) where a and b are operands(variables) and op is Operator.
- Example 1 : A + B
- Example 2 : A * B + C / D
Postfix Notation
Postfix is notation that compiler uses/converts to while reading left to right and is of format AB+ type. The general form can be classified as (ab op) where a and b are operands(variables) and op is Operator.
- Example 1 : AB+
- Example 2 : AB*CD/+
Prefix Notation
Prefix is notation that compiler uses/converts to while reading right to left (some compilers can also read prefix left to right) and is of format +AB type. The general form can be classified as (op ab) where a and b are operands(variables) and op is Operator.
- Example 1 : +AB
- Example 2 : +*AB/CD






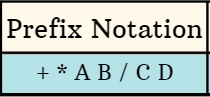
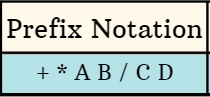
Why Postfix/Prefix Expressions are faster than Infix?
For Infix Expression which is format A+B*C, if the compiler is reading left to right then it can’t evaluate A+B first until it has read whole expression and knows expression is actually A + (B*C) i.e. B * C needs to be implemented first
Postfix for above infix is ABC*+. Now, as soon as compiler sees two operands followed by operator it can implement it without caring for precedence.
- Assume ABC*+
- ABC*+ (BC* is implemented as B*C and result is put back)
- AX+ (Assuming X stores result of BC* i.e. B*C)
- Now finally AX+ can be implemented as A+X
Compiler converts infix expression to postfix/prefix at compile time, so at runtime your calculations are always happening in post-prefix. A website's code maybe compiled once a week but it may need to run 1 million times a week.
Which is why we prefer that runtime execution should be as fast as possible. If calculations happen faster than we have optimized our page load time hugely right?
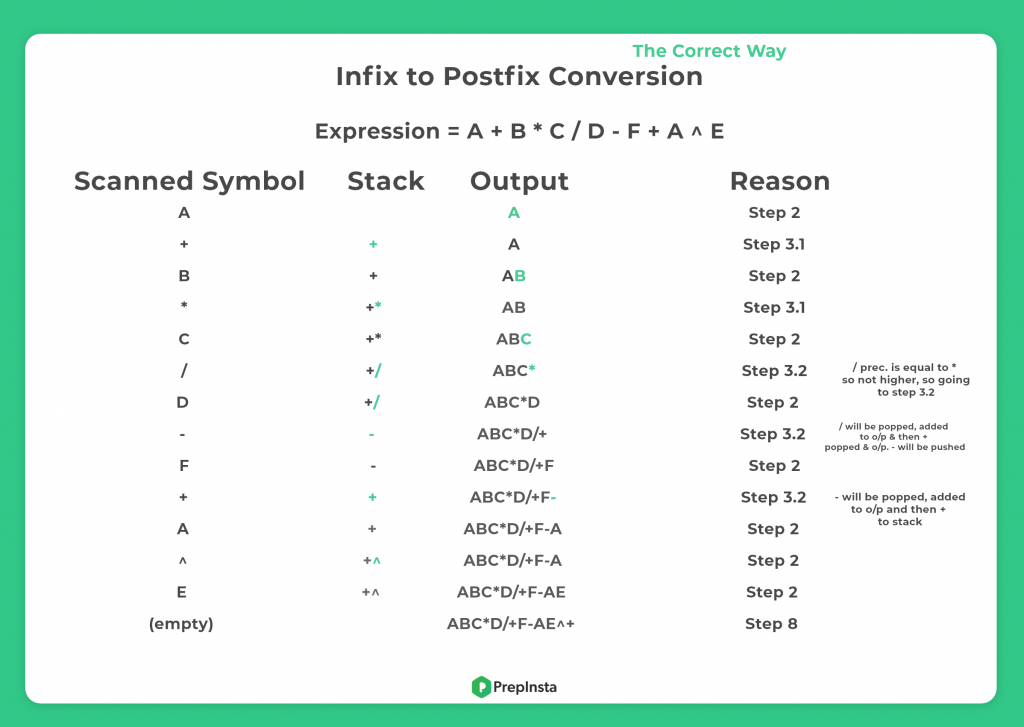
Problem (This is how to convert manually for MCQ Question in the exam)
Problem
- Infix:
a + b * c + dcan be written asa + (b * c) + d - Now, for all + – / * associativity is left to right we will write it as
(a + (b * c)) + dand thus further((a + (b * c)) + d)- Solving and converting innermost bracket to postfix
- Step 1 –
((a + bc*)+ d) - Step 2 – Consider
bc*as separate operandxthe innermost bracket now looks like((a + x)+ d)- Applying postfix it looks like –
(ax+ + d)replacing x here(abc*+ + d)
- Applying postfix it looks like –
- Step 3 – Considering
abc*+as separate operand z, the final bracket looks like –(z + d)the result would bezd+- replacing z value =
abc*+d+
- replacing z value =
Alert
The above may give wrong results sometimes, which is why its always safer to use below algorithm for both coding and manual calculation -Also note below algorithm is given wrong on Geeks4Geek website, only refer from here.(As most codes are made by interns and PrepInsta pages are made by Ph.D Teachers)
Algorithm (For Code/Manual Calculation)
- First Start scanning the expression from left to right
- If the scanned character is an operand, output it, i.e. print it
- Else
- If the precedence of the scanned operator is higher than the precedence of the operator in the stack(or stack is empty or has'(‘), then push operator in the stack
- Else, Pop all the operators, that have greater or equal precedence than the scanned operator. Once you pop them push this scanned operator. (If we see a parenthesis while popping then stop and push scanned operator in the stack)
- If the scanned character is an ‘(‘, push it to the stack.
- If the scanned character is an ‘)’, pop the stack and output it until a ‘(‘ is encountered, and discard both the parenthesis.
- Now, we should repeat the steps 2 – 6 until the whole infix i.e. whole characters are scanned.
- Print output
- Do the pop and output (print) until stack is not empty

Infix to Prefix
Problem (This is how to convert manually for MCQ Question in the exam)
- Infix:
(a / b + c) - ( d + e * f)can be written as((a / b) + c) - ( d + (e * f)) - Now, we have done the above according to associativity
- Solving and converting innermost bracket to prefix
- Step 1 –
(/ab + c) - ( d + *ef) - Step 2 – Consider
/aband*efas separate operandxandy - the innermost bracket now looks like
(x + c) - (d + y)- Applying prefix it looks like –
(+xc - +dy)replacing x and y here(+/abc - +d*ef)
- Applying prefix it looks like –
- Step 3 – Considering
+/abcand+d*efas separate operand z and w, the final bracket looks like –(z - w)the result would be-zw- replacing z and w value =
-+/abc+d*ef
- replacing z and w value =
Alert
The above may give wrong results sometimes, which is why its always safer to use below algorithm for both coding and manual calculation -Also note below algorithm is given wrong on Geeks4Geek website, only refer from here.(As most codes are made by interns and PrepInsta pages are made by Ph.D Teachers)
Algorithm (For Code/Manual Calculation)
Given Infix - ((a/b)+c)-(d+(e*f))- Step 1: Reverse the infix string. Note that while reversing the string you must interchange left and right parentheses.
- Step 2: Obtain the postfix expression of the expression obtained from Step 1.
- Step 3: Reverse the postfix expression to get the prefix expression
This is how you convert manually for theory question in the exam
- String after reversal – ))f*e(+d(-)c+)b/a((
- String after interchanging right and left parenthesis – ((f*e)+d)-(c+(b/a))
- Apply postfix – Below is postfix (On this page you check infix to postfix conversion rule)
- Reverse Postfix Expression (Given After the image below)
| Sr. no. | Expression | Stack | Prefix |
|---|---|---|---|
| 0 | ( | ( | |
| 1 | ( | (( | |
| 2 | f | (( | f |
| 3 | * | ((* | f |
| 4 | e | ((* | fe |
| 5 | ) | ( | fe* |
| 6 | + | (+ | fe* |
| 7 | d | (+ | fe*d |
| 8 | ) | fe*d+ | |
| 9 | – | – | fe*d+ |
| 10 | ( | -( | fe*d+ |
| 11 | c | -( | fe*d+c |
| 12 | + | -(+ | fe*d+c |
| 13 | ( | -(+( | fe*d+c |
| 14 | b | -(+( | fe*d+cb |
| 15 | / | -(+(/ | fe*d+cb |
| 16 | a | -(+(/ | fe*d+cba |
| 17 | ) | -(+ | fe*d+cba/ |
| 18 | ) | – | fe*d+cba/+ |
| 19 | fe*d+cba/+- |
Final prefix: -+/abc+d*ef
Implementation of Infix expression to Postfix expression
#include<stdio.h>
char s[100];
int top_of_stack = -1;
void push(char a)
{
s[++top_of_stack] = a;
}
char pop()
{
if(top_of_stack == -1)
return -1;
else
return s[top_of_stack--];
}
int precedence(char a)
{
if(a == '(')
return 0;
if(a == '+' || a == '-')
return 1;
if(a == '*' || a == '/')
return 2;
}
void main()
{
char expression[20];
char *exp, a;
printf("Enter the expression you want to convert: ");
scanf("%s",expression);
exp = expression;
while(*exp != '\0')
{
if(isalnum(*exp))
printf("%c",*exp);
else if(*exp == '(')
push(*exp);
else if(*exp == ')')
{
while((a = pop()) != '(')
printf("%c", a);
}
else
{
while(precedence(s[top_of_stack]) >= precedence(*exp))
printf("%c",pop());
push(*exp);
}
exp= exp + 1;
}
while(top_of_stack != -1)
{
printf("%c",pop());
}
}
Using Proper Structure
Infix to Postix
// C Program for Implmentation of stack (array) using structure #include <limits.h> #include <stdio.h> #include <stdlib.h> #include <string.h> // A structure to represent a stack struct Stack { int top; int maxSize; // we are storing string in integer array, this will not give error // as values will be stored in ASCII and returned in ASCII thus, returned as string again int* array; }; struct Stack* create(int max) { struct Stack* stack = (struct Stack*)malloc(sizeof(struct Stack)); stack->maxSize = max; stack->top = -1; stack->array = (int*)malloc(stack->maxSize * sizeof(int)); return stack; } // Checking with this function is stack is full or not // Will return true is stack is full else false //Stack is full when top is equal to the last index int isFull(struct Stack* stack) { if(stack->top == stack->maxSize - 1){ printf("Will not be able to push maxSize reached\n"); } // Since array starts from 0, and maxSize starts from 1 return stack->top == stack->maxSize - 1; } // By definition the Stack is empty when top is equal to -1 // Will return true if top is -1 int isEmpty(struct Stack* stack) { return stack->top == -1; } // Push function here, inserts value in stack and increments stack top by 1 void push(struct Stack* stack, int item) { if (isFull(stack)) return; stack->array[++stack->top] = item; } // Function to remove an item from stack. It decreases top by 1 int pop(struct Stack* stack) { if (isEmpty(stack)) return INT_MIN; return stack->array[stack->top--]; } // Function to return the top from stack without removing it int peek(struct Stack* stack) { if (isEmpty(stack)) return INT_MIN; return stack->array[stack->top]; } // A utility function to check if the given character is operand int checkIfOperand(char ch) { return (ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z'); } // Fucntion to compare precedence // If we return larger value means higher precedence int precedence(char ch) { switch (ch) { case '+': case '-': return 1; case '*': case '/': return 2; case '^': return 3; } return -1; } // The driver function for infix to postfix conversion int covertInfixToPostfix(char* expression) { int i, j; // Stack size should be equal to expression size for safety struct Stack* stack = create(strlen(expression)); if(!stack) // just checking is stack was created or not return -1 ; for (i = 0, j = -1; expression[i]; ++i) { // Here we are checking is the character we scanned is operand or not // and this adding to to output. if (checkIfOperand(expression[i])) expression[++j] = expression[i]; // Here, if we scan character ‘(‘, we need push it to the stack. else if (expression[i] == '(') push(stack, expression[i]); // Here, if we scan character is an ‘)’, we need to pop and print from the stack // do this until an ‘(‘ is encountered in the stack. else if (expression[i] == ')') { while (!isEmpty(stack) && peek(stack) != '(') expression[++j] = pop(stack); if (!isEmpty(stack) && peek(stack) != '(') return -1; // invalid expression else pop(stack); } else // if an opertor { while (!isEmpty(stack) && precedence(expression[i]) <= precedence(peek(stack))) expression[++j] = pop(stack); push(stack, expression[i]); } } // Once all inital expression characters are traversed // adding all left elements from stack to exp while (!isEmpty(stack)) expression[++j] = pop(stack); expression[++j] = '\0'; printf( "%s", expression); } int main() { char expression[] = "((a+(b*c))-d)"; covertInfixToPostfix(expression); return 0; }
Output
abc*+d-


Login/Signup to comment