はじめに

　JuliaではPlots.jlやPyPlot.jlなどの描画系ライブラリが比較的充実していますが、GUIでインタラクティブなシミュレーションをするにはまだ確固たる手法がないように思われます。
　そこで、GUIシミュレーションを実現する選択肢の一つとして、ElectronとJuliaを組み合わせ、REPL上でそこその速度で動くインタラクティブなイジングモデルシミュレーションを作ってみました。

JuliaのGUI状況

こちらのサイトGUI Julia Packagesによれば、現在、11種類のGUIパッケージが利用できますが、大きく分けて３つに分かれるようです。

ネイティブライブラリ系(QML.jl, Tk.jl, PySide.jl, JGUI.jl, Qt5.jl, XClipboard.jl)
WEB系(Canvas.jl, Blink.jl, Electron.jl)
IDE依存系(JuliaTools.jl, Table.jl)

この中で、長年メンテナンスされ、比較的実用的なパッケージは

ネイティブライブラリ系(QML.jl, Gtk.jl)
WEB系(Interact.jl(Canvas.jlの後継？), Blink.jl, Electron.jl)

が選択肢として挙がってきますが、

Gtk.jlは公式に非推奨（REPL上でWarningが出る）。
Blink.jl, Interact.jlはWebIO経由での実行が前提で、 REPL上でWebIOを動かすと気が遠くなるほど遅い！。

という問題があり、Jupyter Lab/Notebook上で動かすにはInteract.jlなどで十分ですが（IJuliaがそもそもWebIO経由のため）、REPL上で動かすには実質QML.jlかElectron.jlの２択となります。　
　QMLについてはこちらの記事 JuliaでQtを使ってみる？にまとめられています。そこで、もう一つの選択肢であるElectron.jlでGUIを書いてみたくなった訳です。

Electron+Julia

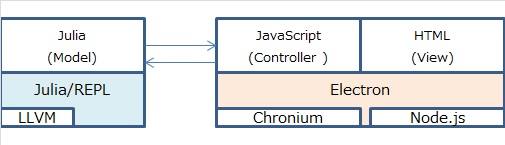
　ElectronはHTML + CSS + JavaScriptのWEB技術でデスクトップアプリをクラスプラットフォームで作成できる優れたフレームワークです。ChromiumブラウザとNode.jsに基づいています。
　JuliaでElectronを利用するライブラリとしてElectron.jlがあり、JuliaとElectronの間をメッセージ通信によりインタラクティブに繋ぐことができます。
　MVCアーキテクチャに基づいて図示するとこんな感じになります。

　Julia上で計算モデル(Model)を実行し、HTML+CSSで画面(View）を実装し、JavaScriptで画面制御(Controller)を行います。こうすることでJuliaの豊富な計算ライブラリを活用しつつ、Electonの豊富なWEBライブラリでGUIを実現してインタラクティブシミュレーションを達成できる訳です。
　ポイントとなるのが、JuliaとElectron(Javascript)との連携ですが、下記で実現します。

Julia->JavaScript: Electron.jlパッケージをJulia側で読み込みHTMLを指定するとウインドウを作成できる。ウインドウオブジェクにメッセージを送るとJavaScriptの関数を呼び出すことができる。
JavaScript->Julia: JavaScript内で"sendMessageToJulia()"関数を呼び出し、Julia側にチャンネル経由でメッセージを送信する(put!()関数)。Julia側ではウインドウに紐づいたチャンネルからtake!()関数で受け取ったメッセージを処理する。

以上のように、実はJulia->JavaScriptとJavaScript->Juliaの関係は非対称です。重要な点はチャンネルを経由し、ElectronとJuliaの並列実行を実現する点です。これによりGUI処理と計算処理を並行して処理できます。
　また、JuliaでJavaScriptの関数を実行できるため、非常に自由度が高いのですが、その分作りこみが必要です。本記事ではMVCの分離の考えから、JuliaとJavaScriptのメッセージ交換はできるだけ少なくするため、数値列での受け渡しとしました。
　他にも、Juliaで画像ファイルを作ってエンコードしたバイナリをJavaScriptに表示させる、といった方法も考えられますが、チャンネルの通信が増えると実行速度が遅くなる傾向があるようです。（実はREPL上でBlink+WebIOを動かすと大量の通信が発生している模様。）

シミュレーション

　今回、シミュレーションの対象とするのは下記の記事で書いたイジングモデルを扱います。

Juliaで非正方格子のイジングモデルをシミュレーションしてみた
諸々のテクニックでJuliaコードを高速化してみたら５０倍以上速くなった件　　ここで、イジングモデルの数式を簡単に示します。

\begin{array}{rcl} E & = & - \sum_{i} \sum_{j \neq i} J_{i j} s_{i} \cdot s_{j} - \sum_{i} H s_{i}, \\ B & = & \frac{1}{N} \sum_{i} ⟨ s_{i} ⟩, \\ P r (E (S)) & = & \frac{e x p (- E (S) / T)}{Z} \end{array}

記号は以下の通りです。

$E$ : 系全体のエネネルギー。
$s_{i}$ : $i$ 番目の原子の（不対電子の）スピン(z軸)。 $s_{i} = + 1, - 1$ の２値をとる。
$N$ : 原子の個数。
$J_{i j}$ : $i$ 番目の原子と $j$ 番目の原子の相互作用係数。
$H$ : 外部磁場との相互作用係数。
$B$ : １スピン当たりの平均磁化。期待値はMCMCにより計算。
$T$ : 温度。

すなわち、外部磁場 $H$ が系の磁化 $B$ に影響を与えるモデルです。シミュレーション条件として、外部磁場 $H$ と温度 $T$ を変化させた際に、系の磁化 $B$ がどう変化するのかを見てみたいと思います。

ソースコード

　それでは、ソースコードを解説していきますが、過去記事と重複する部分は省略します。ソースコードの全体はGitHubにアップロードしてあります。

okimebarun / IsingSimEUI.jl

実行環境：

Julia 1.4.2
パッケージ：Electron, StaticArrays

1. HTML

　まず、ViewとなるHTMLパートです。CSSは省略します。基本的には、ボタンとスライダー、描画用のキャンバスを配置しているだけです。

IsingView01b.html

<!DOCTYPE html>
<html>
<head>
    <meta charset="UTF-8" />
    <title>IsingSim View 1.0</title>
    <link rel="stylesheet" href="./IsingView01b.css">
    <script src="./IsingView01b.js"></script>
</head>
<body>
 <div class="slider-wrapper">
 <fieldset>
 <legend>Control</legend>
 <p>
 <div class="ctlbutton">
     <input type="button" value="start" onclick="animator.start()"></input>
     <input type="button" value="stop"  onclick="animator.stop()"></input>
 </div>
 </p>
 <p>
 <input id="range01" type="range" value="1" min="0.05" max="8" step="0.05" size="400"
  oninput="slider01changed(this.value)" />
 <label id="lrange01" for="temp">T=</label>
 <input id="range02" type="range" value="0" min="-1" max="1" step="0.1" size="400"
  oninput="slider02changed(this.value)" />
 <label id="lrange02" for="temp">H=</label>
 </p> 
 </fieldset>
 </div>

 <div class="canvas-left">
     <fieldset>
     <legend>Spin State</legend>
     <canvas id="myCanvas01" width="400" height="400" style="background-color:black;"></canvas>
     </fieldset>
 </div>
 <div class="canvas-right">
     <fieldset>
     <legend>BH Curve</legend>
     <canvas id="myCanvas02" width="400" height="400" style="background-color:black;"></canvas>
     </fieldset>
 </div>
</body>
</html>

2. JavaScriptコード

　ControllerとなるJavaScriptパートです。いくつかクラスを定義しています。

DrawBox: 描画用のクラスです。Juliaから呼び出し描画を行います。
ControlInfo: スライダーのパラメータ情報を保持するクラスです。
Trajectory: BH曲線の履歴を保持するクラスです。
Animator: アニメーション用のクラスです。定周期(800[ms])でJulia側にパラメータを渡して計算させます。sendMessageToJulia関数に'calc T:{T} H:{H}'という書式で文字列のメッセージを送っています。

IsingView01b.js

window.addEventListener('load', init);

function init() {
    //
    drawbox01 = new DrawBox("myCanvas01");
    drawbox02 = new DrawBox("myCanvas02");
    ctlinfo = new ControlInfo();
    animator = new Animator();
    trajectory = new Trajectory();

    //
    slider01changed(1);
    slider02changed(0);
    //
}

async function slider01changed(v) {
    const range01  = document.getElementById("range01");
    const lrange01 = document.getElementById("lrange01");

    ctlinfo.T = v;
    lrange01.textContent = "T= "+v;
    sendMessageToJulia('T: '+v);
}

async function slider02changed(v) {
    const range02  = document.getElementById("range02");
    const lrange02 = document.getElementById("lrange02");

    ctlinfo.H = v;
    lrange02.textContent = "H= "+v;
    sendMessageToJulia('H: '+v);
}

//////////////////////////////////////////////////////////////////

class DrawBox {
    constructor(canvasId) {
        this.canvas = document.getElementById(canvasId);
        this.ctx = this.canvas.getContext('2d');
        //
        this.rminx = 0;
        this.rmaxx = this.canvas.width;
        this.rminy = 0;
        this.rmaxy = this.canvas.height;
    }
    //
    setrange(minx, maxx, miny, maxy)
    {
        this.rminx = minx;
        this.rmaxx = maxx;
        this.rminy = miny;
        this.rmaxy = maxy;
    }
    //
    convpx(x)
    {
        return Math.floor(this.canvas.width * ( x - this.rminx ) / (this.rmaxx - this.rminx));
    }
    convpy(y)
    {
        return Math.floor(this.canvas.height * ( this.rmaxy - y ) / (this.rmaxy - this.rminy));
    }
    clear() {
        var ctx    = this.ctx;
        var canvas = this.canvas;

        ctx.clearRect(0, 0, canvas.width, canvas.height);
    }
    drawPoly02(poly, ndiv ) {
        //poly : [x,y, x,y, x,y.....];
        var ctx    = this.ctx;
        var canvas = this.canvas;

        ctx.strokeStyle = '#fff';
        ctx.fillStyle = '#f00';

        ctx.beginPath();
        ctx.moveTo( this.convpx(poly[0]), this.convpy(poly[1]) );
        for(var item=2 ; item < poly.length-1 ; item+=2 ){
            if (item % (ndiv*2) == 0) {
                ctx.closePath();
                ctx.fill();
                ctx.beginPath();
                ctx.moveTo( this.convpx(poly[item]) , this.convpy(poly[item+1]) );
            } else {
                ctx.lineTo( this.convpx(poly[item]) , this.convpy(poly[item+1]) );
            }
        }

        ctx.closePath();
        ctx.fill();
        ctx.stroke();
    }
    drawLine( points ) {
        var ctx    = this.ctx;
        var canvas = this.canvas;

        ctx.clearRect(0, 0, canvas.width, canvas.height);

        ctx.strokeStyle = '#f00';

        ctx.beginPath();
        ctx.moveTo( this.convpx(points[0]), this.convpy(points[1]) );
        for(var item=2 ; item < points.length-1 ; item+=2 ){
            ctx.lineTo( this.convpx(points[item]) , this.convpy(points[item+1]) );
        }

        ctx.stroke();
    }
}

class ControlInfo {
    constructor() {
        this.T = 1;
        this.H = 1;
    }
    toString() {
        return "T:" + this.T + ",H:" + this.H;
    }
}

class Trajectory {
    constructor() {
        this.maxn = 100;
        this.num = 0;
        this.xys = [];
    }
    add(x, y) {
        this.xys.push(x);
        this.xys.push(y);
        if (this.xys.length > 2*this.maxn) {
            this.xys.shift();
            this.xys.shift();
        }
    }

}

class Animator {
    constructor() {
        this.sleep = 800; // [ms]
    }
    start() {
        this.timerId = setInterval(this.update, this.sleep);
    }
    stop() {
        clearInterval(this.timerId);
    }
    update() {
        console.log("ctlinfo: " + ctlinfo.toString());
        drawbox02.drawLine(trajectory.xys);
        sendMessageToJulia('calc T:'+ctlinfo.T+' H:' +ctlinfo.H);
    }
}

3. Juliaコード

　ModelとなるJuliaパートです。SquareLatticeModel, HexaLatticeModel, IsingMCMCのモジュールは過去記事とほぼ同じ（一部修正）です。

jscmd: JavaScriptのコマンドを実行します。
winmain: ウインドウのメインループです。チャンネルからのメッセージを待機し、メッセージが来たら正規表現でパラメータを抽出し、計算関数を実行します。計算が終了したらjscmd関数で先ほどのDrawBoxクラスのメソッドを呼び出します。Juliaで作った配列を文字列に変換してdrawPoly02関数に渡しています。また、ウインドウサイズを変えるにはElectronAPIを使います。

IsingSimEUI.jl

module IsingSimEUI

###################################################################################################
# load libraries
using Electron

# load local modules
include("HexaLatticeModel03a.jl")
include("SquareLatticeModel03a.jl")
include("IsingMCMC04a.jl")

###################################################################################################
# prepare
# setting for energy function

function genInitialJH(d=d)
    Jd = [Dict{Int,Int8}() for i in 1:d.N]
    Hd = zeros(Float32, d.N)
    (Jd, Hd)
end

function setJH!( Jd=Jd, Hd=Hd, d=d)
    J0 = 1
    H0 = 0
    for i in 1:d.N
        for j in getNeighbors(i,d)
            @inbounds Jd[i][j] = J0
        end
        @inbounds Hd[i] = H0
    end
end

function setH!(H0, Hd=Hd, d=d)
    @simd for i in 1:d.N
        @inbounds Hd[i] = H0
    end
end

###################################################################################################
# JS command

function jscmd(cmd, win=win)
    run(win, cmd)
end

function drawBH(H, S, d=d, N=N)
    x = H
    y = sum(S)/N
    jscmd("drawbox02.setrange(-1.1,1.1,-1.1,1.1);")
    jscmd("trajectory.add($(x), $(y) );")
end

function drawSim02(snap, d=d, N=N)
    jscmd("drawbox01.setrange(0,$(d.ncols),0,$(d.nrows));")

    (xs,ys) = genPoly(1, d)
    len = length(xs)
    ps = zeros(len*2*N)
    i1 = 0 
    @inbounds @simd for i in 1:N
        # bits
        (xs,ys) = genPoly(i, d)
        if (snap[i] == 1) # up-spin
            for i in 0:(len-1)
                ps[i*2 + 1 + i1*len] = xs[i + 1]
                ps[i*2 + 2 + i1*len] = ys[i + 1]
            end
            i1 += 2
        else # down-spin
        end
    end
    jscmd("drawbox01.clear();")
    jscmd("drawbox01.drawPoly02($(string(ps)), $(string(len)) );")
end

###################################################################################################
# setting for model
d = SquareLatticeModel.ParamDict(128,128,0)
N = d.nrows * d.ncols
d.N = N

###################################################################################################
# simulation main

main_html_uri = string("file:///", replace(joinpath(@__DIR__, "IsingView01b.html"), '\\' => '/'))

function winmain(mdlno)
    ##########
    # setting for simulation
    trial = 10^5 # MCMC trial

    # gen functors as global
    global getNeighbors, genPoly
    if mdlno == 1
        (getNeighbors, genPoly)= SquareLatticeModel.genFunctor(d)
    elseif mdlno == 2
        (getNeighbors, genPoly)= HexaLatticeModel.genFunctor(d)
    end

    # generate Jd, Hd
    (Jd, Hd) = genInitialJH(d)
    setJH!(Jd, Hd)

    # simulation
    global E, initS, MCMC
    (E, initS, MCMC) = IsingMCMC.genFunctor(Jd, Hd)
    S = ones(Int8, N)
    initS(S, N)

    ##########
    global win
    win = Window( URI(main_html_uri))
    ElectronAPI.setBounds(win, Dict("width"=>1050, "height"=>700))
    ch = msgchannel(win)

    while true
        local msg, jscmd
        try
            msg = take!(ch)
        catch
            println("channel closed.")
            break
        end

        m = match(r"^calc T:(?<T>[\d\.]+) H:(?<H>[-\d\.]+)", msg)
        if !(m === nothing)
            T = parse(Float32, m[:T])
            H = parse(Float32, m[:H])
            print("calc with T=$(T) & H=$(H)")
            setH!(H, Hd, d)
            #
            @time (simE) = MCMC(S, T, N, trial);
            drawSim02(S)
            drawBH(H, S)
        end
    end
end

###################################################################################################
# main functions for PackageCompiler

function julia_main()
    try
        real_main()
    catch
        Base.invokelatest(Base.display_error, Base.catch_stack())
        return 1
    end
    return 0
end

#
function real_main()
    @show ARGS
    @show Base.PROGRAM_FILE

    # do something
    winmain(1)
end

if abspath(PROGRAM_FILE) == @__FILE__
    real_main()
end
#
end # module

実はPackageCompiler.jlの書き方に準拠しているのでbuild.jlを定義してあげればコンパイル可能です。ただし、Electronも同時配布する必要があり、サイズが数百MBを超えるため、あまりバイナリ配布には向いていないでしょう。

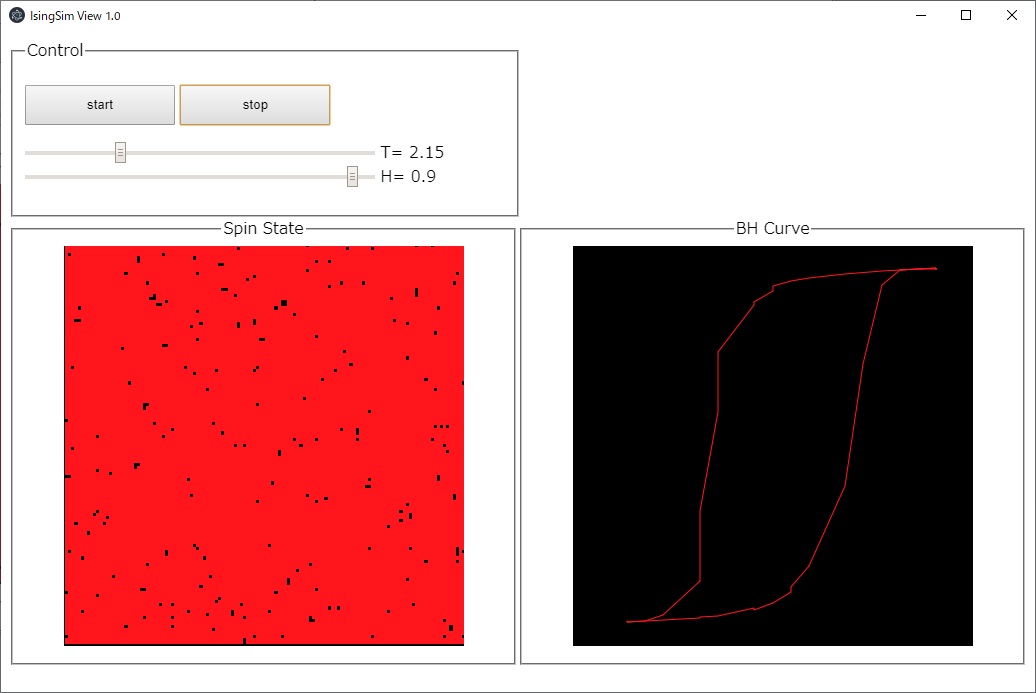
シミュレーション結果

　startボタンを押して計算を開始し、スライダーTやスライダーHを動かして変化する様子を見てみましょう。stopボタンで一時停止できます。外部磁場 $H$ の動かし方でヒステリシスが生じる様子が確認できます。ヒステリシスは、外部磁場のスライダー操作(1->0->-1->0->1)の履歴によって、到達する磁化 $B$ の値が変わることを指します。

この磁化のヒステリシスがあるおかげでHDDなどの磁気ディスクに情報（ビット）を記録できる訳です。また、温度 $T$ を変化させると、スピン状態が変化し、ヒステリシスにも影響を与えることが確認できるでしょう。色々とスライダーを触ると面白いですよ。

JuliaのGUIについて

相転移や分岐ではパラメータが重要なので、インタラクティブシミュレーションで分かることも多いと思います。
今回、Electron側の描画を自前で作りこみましたが、JavaScriptの描画ライブラリを使えば、もっと楽できると思います。
REPL上でもそこそこ動くので、Electronを使えばちょっとしたお試しシミュレーションが楽しく作れるでしょう。
将来的には、Juliaをサーバー上で動かしブラウザでシミュレーションを実行できるフレームワークがもっと充実するといいですね。サーバーで複数のクライアントに対応したり、WEB経由での双方向通信をもっとスマートにできると嬉しいのですが。

参考リンク

下記のぺージを参考にさせて頂きました。

ElectronとJuliaでインタラクティブシミュレーション